Введение понятия процент
Понятие процент вводится после изучения десятичных дробей в 9 классе СКШ VIII вида. Формирование знаний о проценте опирается на знания об обыкновенных и десятичных дробях и на знания соотношений единиц измерения величин метрической системы. Школьники вспоминают соотношение таких единиц измерения, единичное отношение которых равно 100: 1 м = 100 см. Они выражают 1 см в метрах: 1 см = Аналогично рассматривается соотношение единиц измерения массы и стоимости: 1 ц = 100 кг, ⇒1 кг = 1 р. = 100 к., ⇒1 к. = Внимание учащихся обращается на то, что в каждом случае получилась Исходя из этого, можно сказать, что 1 см, равный В данном случае в процентах были выражены числа, полученные при измерении величин. Школьникам следует показать, что и отвлеченные числа могут быть выражены в процентах.
Выражение целых чисел в процентах В основу объяснения положено определение понятия процент: - 1% - это - Все число в 100 раз больше, т.е.: - Значит, если - Сколько процентов составляет число 2? - Т.к. 1 = 100%, а число 2 – в 2 раза больше 1, то 2 = 200%. - Число 8 в 8 раз больше 1, ⇒8 = 800%; - 16 = 1600 % и т.д. На основе полученных знаний школьники знакомятся с понятиями производительность труда, выполнение и перевыполнение нормы. Следует объяснить, что в быту и на производстве часто используется выражение «выполнил норму на 100%». Оно означает, что человек выполнил всю работу, которая была запланирована. Например, пекарь выпек столько буханок хлеба, сколько было запланировано изначально. Перевыполнить норму – это значит сделать больше запланированного, больше 100%, например, выпечь больше буханок хлеба, чем было запланировано. Не выполнить норму – это значит сделать меньше, чем было запланировано, меньше 100%.
Выражение десятичных дробей в процентах
В основе объяснения также как и в предыдущем случае, лежит определение понятия процент: - На основе рассуждений, наблюдений, сравнений десятичных дробей и чисел, выражающих эти дроби в процентах учащиеся подводятся к тому, что заменить дробь процентами – значит узнать, сколько в ней содержится сотых долей. Учащимся предлагается сравнить десятичную дробь и полученное число процентов. Они убеждаются в том, что запятая каждый раз переносится на два знака вправо. Формулируется правило: чтобы десятичную дробь заменить процентами, надо перенести запятую на два знака вправо и записать знак %. Если знаков в числе не хватает, то ставятся нули: 1,6 = 1,60 = 160%, ⇒1,6 = 160%; 2,4 = 240% и т.д.
Выражение обыкновенных дробей в процентах
Выражение дробей со знаменателем 100 в процентах не представляет особых трудностей, так как число процентов оказывается равным числителю таких дробей: Если же знаменатель обыкновенной дроби не равен 100, то ее надо преобразовать в десятичную дробь и применить правило выражения десятичных дробей в процентах:
Выражение процентов в десятичных или обыкновенных дробях (обратное преобразование)
1% = 50% = 100% = 1. 200% в 2 раза больше, ⇒200% = 2; 500% = 5; 120% = Учащимся предлагается сравнить исходное число процентов и полученные обыкновенные дроби. Устанавливается, что в числителе обыкновенной дроби записывается число процентов, а знаменатель дроби равен 100. если необходимо, выполняются преобразования. Знак процентов не пишется. Формулируется правило: чтобы выразить проценты обыкновенной дробью, нужно в знаменателе записать 100, а в числителе записать число процентов. Знак процентов не писать. При сравнении процентов и получившихся десятичных дробей или целых чисел устанавливается, что каждый раз запятая перемещается на два знака влево, а знак процентов не записывается. Формулируется правило: чтобы выразить проценты десятичной дробью или целым числом, надо запятую перенести на два знака влево и знак процентов не писать.
|

 м = 0,01 м.
м = 0,01 м.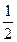 - половина,
- половина, 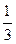 - треть;
- треть;  - четверть. Особое название имеет и
- четверть. Особое название имеет и 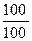 = 1.
= 1. в 2 раза больше, поэтому
в 2 раза больше, поэтому  = 15%;
= 15%; 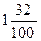 =
= 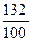 = 132% и т.д.
= 132% и т.д. ;
;  .
. ;
;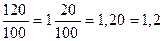 и т.д.
и т.д.


