Методика решения задач на проценты
Существует несколько типов задач на проценты:
1. Нахождение одного или нескольких процентов от числа.
2. Нахождение числа по одному и нескольким его процентам.
3. Задачи на процентное соотношение чисел.
В скш решаются задачи на нахождение одного или нескольких процентов от числа и на нахождение числа по одному его проценту. Остальные задачи не решаются.
Решение задач на проценты основано на умении решать задачи на части. Особое внимание обращается на то, что 1% составляет Сначала учащиеся знакомятся с задачами на нахождение 1% от числа. Перед тем как предложить учащимся задачи, необходимо сформировать у них умение вычислять 1% от числа. Например, требуется найти 1% от 500. Рассуждения: 1% = Затем учащиеся тренируются в нахождении 1% от различных чисел. На основе наблюдений они приходят к выводу: чтобы найти 1% от числа, надо это число разделить на 100. После этого школьникам предлагаются задачи на нахождение 1% от числа. Например: а) В магазин привезли 300 ящиков с цитрусовыми. 1% от всего числа ящиков составляют лимоны. Сколько ящиков лимонов привезли в магазин? Решение: 1% = Аналогично вводятся задачи на нахождение нескольких процентов от числа. Сначала учащимся предлагается найти несколько процентов от отвлеченных чисел. Например, требуется найти 4% от 500. 4% = Итак: 4% = Далее школьники учатся находить несколько процентов от числа. Каждый раз они отвечают на вопросы: «Почему делим на 100?»или «Что получаем, когда делим целое число на 100?»; «Почему умножаем на число процентов?». Формулируется правило: чтобы найти несколько процентов от числа, надо это число разделить на 100 и полученное частное умножить на число процентов. Затем вводятся задачи на нахождение нескольких процентов от числа. Например: В магазине было продано 3200 кг яблок. 20 % от всего числа яблок составили яблоки сорта «Антоновка». Сколько яблок сорта «Антоновка» было продано в магазине? Решение данного типа задач сначала записывается в два действия для того, чтобы учащиеся осознали принцип нахождения нескольких процентов: 1) Сколько килограммов яблок составляет 1%? 3200 кг.: 100 = 32 кг. 2) Сколько килограммов яблок сорта «Антоновка» было продано в магазине? 32 кг. х 20 = 640 кг. После того, как учащиеся станут осознанно подходить к решению таких задач, решение можно записывать в одну строку: 3200 кг.: 100 х 20 = 640 кг. Среди задач на нахождение нескольких процентов от числа встречаются задачи с таким количеством процентов, которое можно заменить обыкновенной дробью. Такие задачи сводятся к задачам на нахождение дроби от числа: 2% = 5% = 10% = Таким образом, вышерассмотренная задача может решаться в одно действие: 20% =
Объяснение решения задач на нахождение числа по одному его проценту дается в сравнении с задачами на нахождение 1% от числа. Например, учащиеся уже умеют решать задачи на нахождение 1% от числа. Им предлагается решить такую задачу: В школе 3000 учащихся. 1% из них – отличники. Сколько отличников в школе? Решение: 1% от 3000 уч. – это 3000 уч.: 100 = 30 уч. Затем формулируется обратная задача (на нахождение числа по 1%): В школе 30 отличников, что составляет 1% от всех учащихся. Сколько всего учащихся в школе? 30 учащихся – это 1% всех учащихся, а все учащиеся составляют 100%, т.е. их число в 100 раз больше 30, поэтому нужно 30 уч. х 100. Таким образом, если 1% составляет 30 учащихся, то 100% составляет 30 уч. х 100 = 3000 уч. Далее учащиеся тренируются в решении задач на нахождение числа по одному его проценту. На основе наблюдений школьники приходят к выводу: чтобы найти число по одному его проценту, надо известную часть числа, которая составляет 1%, умножить на 100.
Примеры решения остальных типов задач, которые не решаются в скш VIII вида Задачи на нахождение числа по нескольким его процентам: Правило: чтобы найти число по его процентам, достаточно известную часть числа разделить на число процентов и результат умножить на 100.
Например: В четырех первых классах 50 девочек, что составляет 25% от всех учащихся первых классов. Сколько всего учащихся первых классов? Решение: 1) Сколько учащихся содержится в 1%? 50 уч.: 25 = 2 уч. 2) Сколько всего учащихся первых классов? 2 уч. х 100 = 200 уч. Т.е.: 50 уч.: 25 х 100 = 200 уч.
|

 часть числа.
часть числа.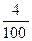 , т.е. надо найти
, т.е. надо найти 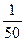 ; 20% =
; 20% = 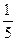 75% =
75% = 
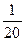 25% =
25% = 
 50% =
50% =