| День
| №№ урока
| Время
| Группа
| Предмет
| № кабинета
|
| ПОНЕДЕЛЬНИК
|
| 08.30-09.10
| АН2
| Английский язык
|
|
|
| 09.30-10.10
| ИНФ2
| Информатика и ИКТ
|
|
|
| 10.25 - 11.05
| МА2
| Алгебра и начала анализа
|
|
|
| 11.15-11.55
| ОБЩ2
| Обществознание
|
|
|
| 12.05-12.45
| | Литература
|
|
|
| 13.00-13.40
| | Физическая культура
| СЗ
|
|
| 13.50-14.30
| | География
|
|
| |
| ВТОРНИК
|
| 08.30-09.10
| РУ2
| Русский язык
|
|
|
| 09.30-10.10
| АН2
| Английский язык
|
|
|
| 10.25 - 11.05
| ОБЩ2
| Обществознание
|
|
|
| 11.15-11.55
| ФИ2
| Физика
|
|
|
| 12.05-12.45
| ОБЩ2
| ЭК «Теория и практика анализа художественного текста»
|
|
|
| 13.00-13.40
| | История
|
|
|
| 13.50-14.30
| | | |
| |
| СРЕДА
|
| 08.30-09.10
| АН2
| Английский язык
|
|
|
| 09.30-10.10
| МА2
| Алгебра и начала анализа
|
|
|
| 10.25 - 11.05
| РУ2
| ЭК «Теория и практика анализа художественного текста»
|
|
|
| 11.15-11.55
| РУ2
| Русский язык
|
|
|
| 12.05-12.45
| | Физическая культура
| СЗ
|
|
| 13.00-13.40
| | География
|
|
|
| 13.50-14.30
| | | |
| |
| ЧЕТВЕРГ
|
| 08.30-09.10
| БИ2
| Биология
|
|
|
| 09.30-10.10
| МА2
| Геометрия
|
|
|
| 10.25 - 11.05
| ХИ2
| Химия
|
|
|
| 11.15-11.55
| ОБЩ2
| Обществознание
|
|
|
| 12.05-12.45
| ОБЩ2
| Обществознание
|
|
|
| 13.00-13.40
| | История
|
|
|
| 13.50-14.30
| | МХК
|
|
| |
| ПЯТНИЦА
|
| 08.30-09.10
| | | |
|
| 09.30-10.10
| РУ2
| Русский язык
|
|
|
| 10.25 - 11.05
| МА2
| Алгебра и начала анализа
|
|
|
| 11.15-11.55
| ФИ2
| Физика
|
|
|
| 12.05-12.45
| | ОБЖ
|
|
|
| 13.00-13.40
| | Литература
|
|
|
| 13.50-14.30
| | Литература
|
|
Кл. рук.: Емельянова Татьяна Александровна 8 (916) 958 25 96 (кабинет 229)
Электрическое поле при наличии проводников.
Удельное сопротивление (проводимость) веществ определяет классификацию материалов по трем основным типам: диэлектрики, полупроводники, металлы. Классификация производится по следующим пределам изменения удельного сопротивления  :
:
а) диэлектрики:  Ом×м;
Ом×м;
б) полупроводники:  Ом×м;
Ом×м;
в) металлы  Ом×м.
Ом×м.
Можно определить эту классификацию по удельной проводимости  (Ом-1×м-1=См×м, См - Сименс).
(Ом-1×м-1=См×м, См - Сименс).
В металлах существуют свободные носители электрических зарядов – свободные электроны, определяющие большую проводимость, так как при наличии электрического поля возникает ток – направленное движение зарядов. Сила тока связана с разностью потенциалов законом Ома, отрытым экспериментально в 1827г.:
 , (2.1)
, (2.1)
где  – сопротивление:
– сопротивление:  ,
,  - длина проводника,
- длина проводника,  - его сечение,
- его сечение,  - разность потенциалов. Если записать
- разность потенциалов. Если записать  , где
, где  - вектор плотности тока, то:
- вектор плотности тока, то:
 ;
;  ,
,
получим закон Ома в векторной форме.
 (2.2)
(2.2)
В электростатике рассматривается случай неподвижных зарядов, т.е.  , поэтому
, поэтому  :
:
внутри проводника при электростатическом равновесии электрическое поле отсутствует.
Используя теорему Гаусса:
 ,
,
 при
при  получим
получим 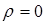 , то есть внутри проводника отсутствуют объемные заряды. Конечно, внутри проводника имеются как положительные, так и отрицательные заряды, но они взаимно компенсируются, так что внутри проводника
, то есть внутри проводника отсутствуют объемные заряды. Конечно, внутри проводника имеются как положительные, так и отрицательные заряды, но они взаимно компенсируются, так что внутри проводника 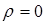 . Если нейтральный проводник поместить во внешнее электрическое поле, то поверхностные заряды на нем перераспределяются так, что создаваемые ими внутри электрические поля компенсируют внешнее поле. Если
. Если нейтральный проводник поместить во внешнее электрическое поле, то поверхностные заряды на нем перераспределяются так, что создаваемые ими внутри электрические поля компенсируют внешнее поле. Если  - внешнее поле,
- внешнее поле,  - поле, создаваемое поверхностными зарядами, то (рис.2.1)
- поле, создаваемое поверхностными зарядами, то (рис.2.1)

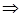
 . (2.3)
. (2.3)
Явление перераспределения поверхностных зарядов на проводнике при его помещении во внешнее электрическое поле называется электрической индукцией.
Поле вблизи поверхности проводника.
 Найдем поле вблизи поверхности проводника (рис.2.2). Для этого используем теорему Гаусса. Выберем гауссову поверхность в виде цилиндра с основанием
Найдем поле вблизи поверхности проводника (рис.2.2). Для этого используем теорему Гаусса. Выберем гауссову поверхность в виде цилиндра с основанием  . Тогда поток напряженности поля, создаваемого поверхностными зарядами
. Тогда поток напряженности поля, создаваемого поверхностными зарядами  :
:

где  - заряд в объеме цилиндра. Направим
- заряд в объеме цилиндра. Направим  по нормали к поверхности проводника. Поток вектора
по нормали к поверхности проводника. Поток вектора  через поверхность:
через поверхность:
 Þ
Þ  . (2.4)
. (2.4)
Нормальная составляющая вектора напряженности электрического поля вблизи поверхности проводника определяется поверхностной плотностью заряда.
 Поле
Поле  представляет собой сумму двух полей: на границе диэлектрика есть поле
представляет собой сумму двух полей: на границе диэлектрика есть поле  , создаваемое зарядами на границе, (оно направлено как наружу, так и вовнутрь металла); кроме того, есть внешнее поле
, создаваемое зарядами на границе, (оно направлено как наружу, так и вовнутрь металла); кроме того, есть внешнее поле  , направленное лишь в одну сторону. Из рис.2.3 видно, что внутри поля
, направленное лишь в одну сторону. Из рис.2.3 видно, что внутри поля  и
и  компенсируются; снаружи
компенсируются; снаружи  и
и  складываются и образуют поле
складываются и образуют поле  . Учитывая равенство поля внутри проводника нулю, получаем:
. Учитывая равенство поля внутри проводника нулю, получаем:
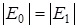 .
.
 Для нахождения тангенциальной составляющей вектора
Для нахождения тангенциальной составляющей вектора  воспользуемся теоремой о циркуляции. Выберем прямоугольный контур 1 – 2 – 3 – 4 (рис.2.4).
воспользуемся теоремой о циркуляции. Выберем прямоугольный контур 1 – 2 – 3 – 4 (рис.2.4).
 .
.
Внутри  ; на участках 14 и 23
; на участках 14 и 23  . Тогда:
. Тогда:
 ,
,
 . (2.5)
. (2.5)
Это означает, что:
напряженность электрического поля вблизи поверхности проводника направлена по нормали к поверхности и равна  .
.
 . (2.6)
. (2.6)
Зависимость поверхностной плотности зарядов от кривизны.
Рассмотрим систему из двух проводящих шаров, заряженных зарядами  и
и 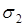 . Радиусы шаров
. Радиусы шаров  и
и  . Если шары не соединены друг с другом, то
. Если шары не соединены друг с другом, то
 ;
;  ;
;
 ;
; 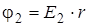 .
.
Соединим их проволокой, тогда 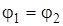 ;
;  , т.е.
, т.е.
 , (2.7)
, (2.7)
поверхностная плотность больше на шаре с меньшим радиусом. Можно заключить, что поверхностная плотность зарядов увеличивается с ростом кривизны поверхности. Это проявляется в стекании заряда с острия, в таком явлении, как огни Эльма.
Так как внутри проводника  , то внутренняя часть его может быть удалена: остается замкнутая оболочка, называющаяся экраном (экранирует внутреннее пространство от внешних полей) - см.рис.2.5. Техническое использование экранов из сетки очень широкое.
, то внутренняя часть его может быть удалена: остается замкнутая оболочка, называющаяся экраном (экранирует внутреннее пространство от внешних полей) - см.рис.2.5. Техническое использование экранов из сетки очень широкое.

 Можно ли использо-вать экран для того, чтобы поле не проникало наружу, во внешнее пространство?
Можно ли использо-вать экран для того, чтобы поле не проникало наружу, во внешнее пространство?
Поместим положительный заряд  внутри экрана (рис.2.6). На внутренней стороне возникнут отрицательные заряды
внутри экрана (рис.2.6). На внутренней стороне возникнут отрицательные заряды  , на внешней – положительные
, на внешней – положительные  . Они обусловливают
. Они обусловливают  , направленные наружу, т.е. вне экрана поле существует. Чтобы было
, направленные наружу, т.е. вне экрана поле существует. Чтобы было  , необходимо заземлить оболочку, т.е. удалить все заряды с внешней оболочки.
, необходимо заземлить оболочку, т.е. удалить все заряды с внешней оболочки.
Заземленная замкнутая оболочка экранирует внешнее замкнутое пространство от зарядов, находящихся в объеме, окруженном этой оболочкой.
Так как на поверхности проводника  ,
,  , то она является эквипотенциальной поверхностью, поскольку
, то она является эквипотенциальной поверхностью, поскольку  направлен по нормали. Потенциал во всех точках проводника постоянен по величине и может быть записан как:
направлен по нормали. Потенциал во всех точках проводника постоянен по величине и может быть записан как:
 . (2.8)
. (2.8)

 :
: Ом×м;
Ом×м; Ом×м;
Ом×м; Ом×м.
Ом×м. (Ом-1×м-1=См×м, См - Сименс).
(Ом-1×м-1=См×м, См - Сименс). , (2.1)
, (2.1) – сопротивление:
– сопротивление:  ,
,  - длина проводника,
- длина проводника,  - его сечение,
- его сечение,  - разность потенциалов. Если записать
- разность потенциалов. Если записать  , где
, где  - вектор плотности тока, то:
- вектор плотности тока, то: ;
;  ,
, (2.2)
(2.2) , поэтому
, поэтому  :
: ,
, при
при 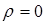 , то есть внутри проводника отсутствуют объемные заряды. Конечно, внутри проводника имеются как положительные, так и отрицательные заряды, но они взаимно компенсируются, так что внутри проводника
, то есть внутри проводника отсутствуют объемные заряды. Конечно, внутри проводника имеются как положительные, так и отрицательные заряды, но они взаимно компенсируются, так что внутри проводника  - внешнее поле,
- внешнее поле,  - поле, создаваемое поверхностными зарядами, то (рис.2.1)
- поле, создаваемое поверхностными зарядами, то (рис.2.1)
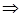
 . (2.3)
. (2.3) Найдем поле вблизи поверхности проводника (рис.2.2). Для этого используем теорему Гаусса. Выберем гауссову поверхность в виде цилиндра с основанием
Найдем поле вблизи поверхности проводника (рис.2.2). Для этого используем теорему Гаусса. Выберем гауссову поверхность в виде цилиндра с основанием  :
:
 - заряд в объеме цилиндра. Направим
- заряд в объеме цилиндра. Направим  по нормали к поверхности проводника. Поток вектора
по нормали к поверхности проводника. Поток вектора  Þ
Þ  . (2.4)
. (2.4) Поле
Поле  представляет собой сумму двух полей: на границе диэлектрика есть поле
представляет собой сумму двух полей: на границе диэлектрика есть поле  , создаваемое зарядами на границе, (оно направлено как наружу, так и вовнутрь металла); кроме того, есть внешнее поле
, создаваемое зарядами на границе, (оно направлено как наружу, так и вовнутрь металла); кроме того, есть внешнее поле  , направленное лишь в одну сторону. Из рис.2.3 видно, что внутри поля
, направленное лишь в одну сторону. Из рис.2.3 видно, что внутри поля  . Учитывая равенство поля внутри проводника нулю, получаем:
. Учитывая равенство поля внутри проводника нулю, получаем: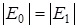 .
. Для нахождения тангенциальной составляющей вектора
Для нахождения тангенциальной составляющей вектора  .
. ; на участках 14 и 23
; на участках 14 и 23  . Тогда:
. Тогда: ,
, . (2.5)
. (2.5) .
. . (2.6)
. (2.6) и
и 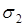 . Радиусы шаров
. Радиусы шаров  . Если шары не соединены друг с другом, то
. Если шары не соединены друг с другом, то ;
;  ;
; ;
; 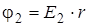 .
.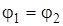 ;
;  , т.е.
, т.е. , (2.7)
, (2.7)
 Можно ли использо-вать экран для того, чтобы поле не проникало наружу, во внешнее пространство?
Можно ли использо-вать экран для того, чтобы поле не проникало наружу, во внешнее пространство? внутри экрана (рис.2.6). На внутренней стороне возникнут отрицательные заряды
внутри экрана (рис.2.6). На внутренней стороне возникнут отрицательные заряды  , на внешней – положительные
, на внешней – положительные  ,
,  направлен по нормали. Потенциал во всех точках проводника постоянен по величине и может быть записан как:
направлен по нормали. Потенциал во всех точках проводника постоянен по величине и может быть записан как: . (2.8)
. (2.8)


