Электрическая емкость проводника. Конденсаторы.
Из формулы (2.8) видно, что
где С – емкость проводника; это коэффициент пропорциональности между зарядом и коэффициентом. В СИ единица емкости – Фарада (Ф). В СГСЕ - единица емкости – сантиметр (см). Примеры. 1. Емкость шара. Чтобы определить емкость шара, нужно найти напряженность поля\ шара и его потенциал:
Тогда:
Конденсатором называется совокупность двух проводников с одинаковыми по величине, но противоположными по знаку зарядами. Емкость двух проводников (конденсатор).
Вычисление емкости конденсатора сводится к нахождению 2. Плоский конденсатор.
(см. теорему Гаусса для плоскости). Снаружи
3. Шаровой конденсатор. Если на внешней и внутренней обкладках сферического конденсатора имеется заряд
Отсюда по формуле (2.11):
4. Цилиндрический конденсатор.
Отсюда:
Так как
Емкость по формуле (2.11):
Соединение конденсаторов.
При последовательном соединении (рис.2.10) заряды на конденсаторах одинаковы, а разность потенциалов на каждом запишется:
|

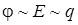 . Рассмотрим уединенный проводник. Потенциал проводника зависит от заряда на его поверхности и может быть записан:
. Рассмотрим уединенный проводник. Потенциал проводника зависит от заряда на его поверхности и может быть записан: , (2.9)
, (2.9) ;
;  .
. . (2.10)
. (2.10) .
. . (2.11)
. (2.11)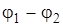 .
. Из рис.2.7 видно, что внутри конденсатора:
Из рис.2.7 видно, что внутри конденсатора: ,
, (2.12)
(2.12) . Тогда:
. Тогда: ;
;  ;
; 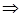
 . (2.13)
. (2.13)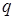 , то:
, то: ;
;  ;
; . (2.14)
. (2.14) Определим
Определим  по теореме Гаусса. Гауссова поверхность – цилиндр (см.рис.2.8). Тогда при
по теореме Гаусса. Гауссова поверхность – цилиндр (см.рис.2.8). Тогда при 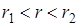 :
: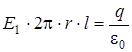 .
. ;
; , то:
, то: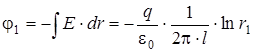 ;
;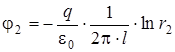 .
. . (2.15)
. (2.15) В случае параллельного соединения (рис.2.9) общий заряд равен:
В случае параллельного соединения (рис.2.9) общий заряд равен:
 (2.16).
(2.16).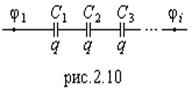

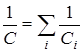 (2.17)
(2.17)


