Теоретическая часть. При вращении звена вокруг оси 𝛧 с угловой скоростью 𝜔 к каждой элементарной точечной массе его будет приложена центробежная сила инерции.
При вращении звена вокруг оси 𝛧 с угловой скоростью 𝜔 к каждой элементарной точечной массе его будет приложена центробежная сила инерции.
Элементарные силы инерции точечных масс всего звена можно свести к главному вектору центробежных сил инерции
где 𝑚 – масса звена, 𝑟𝑠 - расстояние от оси вращения 𝑍 до центра масс неуравновешенного звена, 𝓁𝑖 - расстояние между силами инерции вдоль оси вращения 𝑍. Сила - Для устранения этих вредных последствий необходимо свести к нулю силу Пусть звено массой 𝑚 = 10 кг вращается с постоянной угловой скоростью 𝜔 = 1000 (1/с). Расстояние от оси вращения до центра масс 𝑟𝑠 = 0,001м. Сила веса звена: 𝐹𝜎 = 𝑚𝑞 = 10·10 = 100Н. Сила инерции: 𝐹ин = 𝑚𝑎𝑠 = 𝑚𝜔2𝑟𝑠 = 10·10002·0,001 = 10000Н. Сила инерции в 100 раз больше силы веса. Для полного уравновешивания вращающегося звена необходимо, чтобы главный вектор
Выполнение только первого условия равносильно условию расположения центра масс на оси вращения звена. Такое уравновешивание вращающегося звена называется статическим. Оно применимо для звеньев имеющих малую протяженность вдоль оси вращения (шкивы, маховики и т.п., рисунок 1) Для статического уравновешивания надо в направлении противоположном центру масс установить добавочную (уравновешивающую) массу – 𝑚𝑦𝑝 на расстоянии от оси вращения – 𝑟𝑦𝑝, таким образом, чтобы сила инерции уравновешивающего груза была равна, но противоположна направлена силе инерции неуравновешенного звена: т.е.,
или
Рисунок 1 – Схема балансировки плоского диска
Результирующая сила инерции при этом условии будет равна нулю. То есть, за меру статической неуравновешенности или статического дисбаланса принимают величину статического момента масс звена относительно оси вращения:
Если для широкого барабана выполнить то же самое условие, но уравновешивающую массу установить на расстоянии вдоль оси вращения 𝓁 от центра масс (рисунок 2), то статически барабан будет уравновешен:
Но при вращении появляется момент пары сил инерций:
который также вызывает биения. Для динамической балансировки необходимо выполнить второе условие:
т.е., в плоскости действия
или из равенства:
Звено будет сбалансировано статически и динамически, если равна нулю сумма произведений неуравновешенных масс 𝑚𝑖 на их расстояния от оси вращения 𝑍𝑖 и на расстояния её от произвольной точки на оси вращения до плоскостей вращения этих масс, т.е.:
Рисунок 3 – Установка ТММ-35М
Вращающееся звено (ротор) представляет собой вал 1, на котором свободно посажены, пять алюминиевых дисков 2 на расстоянии 80 мм друг от друга. В осевом направлении диски ограничиваются кольцами 3, жестко закрепленными на валу. Кольца градуированы по образующей через 1 градус, а ступицы дисков имеют риску, позволяющую установить диск под заданным углом. Фиксация дисков осуществляется винтами 4. Диски имеют два сквозных паза: - один для крепления грузов, другой – для уравновешивания диска (пазы расположены под углом 1800). На диске рядом с пазом для крепления грузов привернута шкала, позволяющая установить груз на нужный радиус. По варианту исходных данных (приложение Б) на 2, 3 и 4 диски задаются массы 𝑚2, 𝑚3 и 𝑚4, расстояния от оси вращения до точек их крепления на дисках (радиусы) 𝑟2, 𝑟3 и 𝑟4, углы поворота дисков 𝜑2, 𝜑3 и 𝜑4.(Приложение А, рисунок А.1). Исходные данные занести в таблицу А.1 приложения А. Необходимо определить уравновешивающие массы 𝑚1 и 𝑚5, радиусы 𝑟1 и 𝑟5 и углы поворота 𝜑1 и 𝜑5 для первого и пятого дисков так, чтобы установка была сбалансирована статически и динамически. Это достигается решением двух векторных уравнений, которые необходимо решить графическим и аналитическим методом.
Расчет упрощается если его начать с решения второго уравнения. При этом за точку отсчета удобнее принять точку крепления первого диска, тогда 𝓁1 = 0 и векторное уравнение (6) принимает вид:
|


 приложенному в центре масс звена – 𝑆, и главному моменту (паре сил) инерции -
приложенному в центре масс звена – 𝑆, и главному моменту (паре сил) инерции -  ,
,  Нм, действующих в различных плоскостях:
Нм, действующих в различных плоскостях: , (1)
, (1) , (2)
, (2) и момент -
и момент -  и момент
и момент  ин и главный момент
ин и главный момент 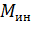 = 0 (4)
= 0 (4)



 ин
ин


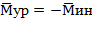






 нужно двумя новыми уравновешивающими грузами 𝑚'𝑦𝑝 создать равный по величине, но противоположно направленный уравновешивающий момент:
нужно двумя новыми уравновешивающими грузами 𝑚'𝑦𝑝 создать равный по величине, но противоположно направленный уравновешивающий момент:










