Графическое решение
Найти модули векторов:
𝑚2𝑟2𝓁2, 𝑚3𝑟3𝓁3, 𝑚4𝑟4𝓁4 (𝑚1𝑟1𝓁1 = 0).
Найти длины векторов в выбранном масштабе, мм
- решая графически уравнение (6) на первом плане векторного уравнения (приложение А, рисунок А.2) найти длину и направление вектора Из конца этого вектора под углом 𝜑3 построить вектор Вектор СО1 есть вектор Модуль:
Произведение:
Значения 𝑚5𝑟5𝓁5, 𝑚5𝑟5 и 𝜑5 занести в таблицу А.1 (приложение А). На втором плане решая графическое уравнение (5) (приложение А, рисунок А.3) от начала координат О2 последовательно построить вектора
Конец последнего вектора (точку Д) соединить с началом координат О2. Вектор ДО2 есть вектор Модуль: Полученные значения Полюсы построения планов О1 и О2 и масштабные коэффициенты выбирать произвольно, так, чтобы графики решения не были мелкими и умещались бы каждый на одной странице отчета.
|
,
𝓁5, мм. Для этого из полюса построения плана – О1 под углом 𝜑₂ от оси 𝑋 против вращения часовой стрелки построить вектор 
(обозначить конец его точкой А).
𝓁3(точка В). Из точки В под углом 𝜑4 построить вектор 
𝓁4 (точка С). Конец последнего вектора (точку С) соединить с началом координат – О1.
, г·мм2.
, 
. Его длину (мм) и направление (угол 𝜑1) замерить на плане построения.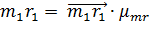
, г·мм.
и 𝜑1 занести в таблицу А.1. (приложение А).
