Теоретическая часть. Дана матрица смежности соответствующего знакового орграфа
Дана матрица смежности соответствующего знакового орграфа. Преобразовать орграф (согласно порядковому номеру в группе) в розу. Исследовать ее на устойчивость. а) В случае наличия неустойчивости найти возможные стабилизирующие стратегии, используя теоремы о связи лепестковой последовательности розы с ее устойчивостью, а также выполнить задания №1, 2 (см. текст л.р.№2). б) В случае отсутствия неустойчивости составить для своего орграфа таблицы, содержащие значения импульсов во всех остальных вершинах и изменения значений в них (см. табл. №1 и №2 в л.р. №2), а также выполнить задания №3 – 5 (см. текст л.р.№2).
Вариант 1
Центральная вершина - С
Вариант 2
Центральная вершина - А
Вариант 3
Центральная вершина - С
Вариант 4
Центральная вершина - A
Вариант 5
Центральная вершина - A
Вариант 6
Центральная вершина - A
Вариант 7
Центральная вершина - С
Вариант 8
Центральная вершина - С
Вариант 9
Центральная вершина - С
Вариант 10
Центральная вершина - A
Вариант 11
Центральная вершина - A
Вариант 12
Центральная вершина - С
Лабораторная работа №3 ИССЛЕДОВАНИЕ ДИНАМИЧЕСКИХ ПРОЦЕССОВ В СЛОЖНЫХ СЭС
Теоретическая часть
Задача управления социально-экономической системой, как правило, очень сложна и трудно формализуема. Однако существуют методы и приемы, призванные упростить ее. Одним из таких методов является моделирование и изучение структурно-функциональных особенностей СЭС в виде орграфов. Особенно удобен этот прием при исследовании систем, аппроксимируемых орграфами с топологией – обобщенная роза. В данной работе использование аппарата орграфов в процессе выработки стратегий управления СЭС будет проиллюстрировано на конкретном примере энергетической системы города, включающей глобальные социальные, экономические и экологические факторы. Масштабную задачу выработки управляющих стратегий для СЭС можно разбить на шесть этапов. Этап 1. Построение модели системы в виде орграфа. Какой тип орграфа будет использован – знаковый (ЗО), взвешенный (ВО) или функциональный (ФО) – зависит от целей моделирования и анализа, а также от конкретных характеристик системы. В нашем случае СЭС представлена в виде ЗО на рис. 3.1.
– – –
+ + +
C – энергетические мощности J – число рабочих мест U – потребление электроэнергии F – количество предприятий R – стоимость энергии Q – состояние окружающей среды P – населенность города Рис. 3.1.
Этап 2. Оценка адекватности выбранного языка описания модели реальным социально-экономическим процессам в сложной системе. Рассматриваемый пример содержит достаточно много упрощений. · Так, воздействия некоторых переменных на другие могут быть различной силы. В частности эффект влияния населенности P на потребление энергии более значителен, чем влияния состояния окружающей среды Q на населенность P. Модель же в виде ЗО предусматривает все воздействия одинаковыми по силе, так как вес каждой дуги равен единице. Возможно, более обоснованно было бы приписывать дугам (u,v) различные веса w(u,v), что приведет к модели ВО. · Еще более реалистично считать, что сила воздействия, соответствующая дуге (u,v) изменяется в зависимости от переменных u и v. Эту зависимость можно продемонстрировать, приписав каждой дуге (u,v) орграфа функцию fuv(u, v). Тогда функция интерпретируется как сила воздействия u на v, если вершина u принимает значение уровня u, а v – значение уровня v. Орграф с такой функцией является функциональным знаковым орграфом. · Следующее упрощение состоит в том, что в модели не учитывается время запаздывания при воздействии изменения в u на v. Например, прирост населения P почти мгновенно влечет за собой рост потребления электроэнергии, а между ростом числа рабочих мест J и привлечением в город дополнительного населения пройдет немалое время. Вообще количество времени, необходимое для воздействия изменения в u на v будет зависеть от дуги (u,v). Таким образом, в более точной модели следует ввести на дуге второй вес для указания запаздывания, соответствующего воздействию, или в более общем виде функцию guv(u, v). Если запаздывания целочисленные, то тривиальное решение можно получить, вставляя ряд дополнительных вершин. Число добавленных вершин будет соответствовать запаздыванию. Однако это не является практичным решением, поскольку полученный орграф может оказаться слишком большим. Несмотря на указанные выше упрощения, применение именно ЗО в данном случае кажется наиболее целесообразным. Наряду с наглядностью и приемлемой степенью соответствия изучаемой сложной социально-экономической системе, он обладает несомненным достоинством – возможностью использовать простые формальные методы анализа. Однако не стоит забывать, что выводы, полученные на основе такого упрощенного анализа, носят не окончательный, а лишь рекомендательный характер. Этап 3. Формулировка изучаемой проблемы. Этот этап является основополагающим. От его результатов зависит дальнейший ход анализа. Поэтому формулировка проблемы должна быть предельно ясной и четкой и по возможности изложенной на языке выбранной модели. Так, полагая, что каждая вершина ui принимает значение (достигает уровня) vi(t) в дискретные моменты времени, проблему прогнозирования потребности в электроснабжении можно сформулировать следующим образом: предсказать значение вершины U в некоторый момент t. Можно ввести ограничения или нормативы, связанные с требованиями окружающей среды, а также ограничения иного происхождения. Это делается путем введения двух векторов: m=<m1,m2,...,mn> и M=<M1,M2,...,Mn>, представляющих соответственно нижние (mi) и верхние (Mi) ограничения на значения параметра вершины ui. В исследуемой модели могут быть ограничены, например, вершины Q и J. Кроме проблемы прогнозирования при анализе СЭС (или СЭП) могут возникать задачи иного характера: – проблема предсказания влияния внешних факторов (например, новых технологий) на устойчивость и функционирование системы; – проблема генерации оптимальной стратегии управления системой; – проблема выбора политики, удовлетворяющей внешним ограничениям. Этап 4. Оценка имеющейся структуры системы с точки зрения поставленной проблемы. Используются понятия четных и нечетных циклов. Четный цикл имеет положительное произведение знаков всех входящих в него дуг, нечетный – отрицательное. Наличие четных циклов является простейшим показателем структурной неустойчивости, так как любое начальное изменение параметра в вершине четного цикла приводит к неограниченному росту модуля параметров в других вершинах. В исследуемой системе присутствуют, к примеру, следующие четные циклы: (C,R,U,C) (C,F,J,P,U,C) (U,R,U) Это позволяет уже на этапе визуальной оценки предположить, что система неустойчива. Например, проанализируем цикл (C,R,U,С). Увеличение по какой-нибудь причине энергетических мощностей повлечет за собой снижение стоимости электроэнергии, что в свою очередь вызовет рост ее потребления, а это потребует дальнейшего увеличения производства энергии. Круг замкнулся, и дальнейшее развитие системы будет идти по нарастающей в сторону увеличения энергетических мощностей, если, конечно, в систему не поступят какие-либо внешние импульсы. Вообще, существует множество способов анализа начальной структуры. Их применение зависит от конкретных целей. Пусть нас интересует изменение состояния окружающей среды под воздействием увеличения потребления электроэнергии. Формально это означает, что импульсный процесс начинается в вершине U. Наша задача определить, каким будет импульс в вершине Q и ее значение в различные моменты времени. Для этого используем теорему о знаковом индексе пути орграфа (см. лабораторную работу №1 теоремы 1 и 2). Таблица 1.
Знаковый индекс пути из U в Q длины не более 4-х равен SUQ(4) = -1 + (-1) + (-1) = -3 Тогда согласно теореме 1: vQ(4) = vQ(исх)+PQ(0)+(-3) = vQ(исх)-3 Этот результат можно интерпретировать следующим образом: если потребление энергии возрастет на 1 в некоторый момент времени t=0 и никаких других воздействий на систему не будет, то состояние окружающей среды будет ухудшаться в моменты t=1,3,4 и уровень состояния окружающей среды в момент t=4 будет на 3 единицы хуже, чем исходное значение. Этап 5. Выработка стратегий. Четвертый этап полезен не только для понимания общего состояния системы. Как правило, уже на этом этапе становятся ясны некоторые возможные стратегии для улучшения ситуации. Под стратегией будем понимать процедуру, изменяющую модель системы. Если система представлена ВО, некоторые возможные стратегии состоят в следующем: – изменить на некоторое время значения некоторых вершин – добавить в заданное время некоторую вершину (фактор) и дуги от нее и к ней – изменить в определенное время знак дуги – изменить вес некоторой дуги – добавить новую дугу к уже имеющимся – добавить новый контур (усиливающий или уменьшающий отклонение) Выше было показано, что четный цикл (U,R,U) является дестабилизирующим фактором. Можно попытаться изменить знак дуги (U,R) с “–” на “+”. Такую стратегию принято называть “обращением структуры расценок”, и она будет заставлять более крупных потребителей энергии платить больше за киловатт-час, а не меньше, как в исходной модели. Другая интересная стратегия состоит в изменении знака дуги (J,P) с “+” на “–”. Этого можно добиться, предоставляя больше рабочих мест женщинам, вынуждая их меньше времени уделять семьям. Представляет интерес также стратегия, состоящая в добавлении дуги со знаком “+” из Q в C. Этим устанавливается связь между допустимыми энергетическими мощностями и индикатором состояния окружающей среды. Чаще всего перед исследователем стоит задача построения такой системы, любое внешнее воздействие на которую не приводит к слишком большим изменениям внутренних переменных. Стратегии, отвечающие такому условию, называют стабилизирующими. Таких стратегий может быть несколько и основная задача – найти оптимальную из них (кратчайшую, самую дешевую и т.п.) Вообще выделяют два подхода к формированию стратегий. Их суть может быть выражена вопросами: · Что будет, если...? · Что сделать, чтобы...? В первом случае сами стратегии определяются неформальными методами, исходя из опыта и представлений экспертов в изучаемом вопросе. В результате применения стратегий изменяется первоначальная топология графа, что должно сказаться на его устойчивости. Дальнейший формальный анализ устойчивости осуществляется на базе следующих теорем (лабораторная работа №1 теоремы 4, 5, 6): Т.4. Если ВО импульсно устойчив для всех простых импульсных процессов, то каждое собственное значение орграфа по абсолютной величине не превосходит единицы. Т.5. Если все ненулевые значения ВО различны и не превосходят по абсолютной величине 1, то ВО импульсно устойчив для любых простых импульсных процессов. Т.6. ВО абсолютно устойчив для любого простого импульсного процесса тогда и только тогда, когда он импульсно устойчив для любого простого импульсного процесса и среди его собственных значений нет равного 1. Проиллюстрируем данный подход на примере анализа стратегии “обращения структуры расценок” и политики, заставляющей некоторые предприятия прекращать работу при строительстве новых электростанций.
Таблица 2.
В первом случае ЗО импульсно и абсолютно неустойчив для некоторого простого импульсного процесса. Т.е. если мы полагаем, что ни одна переменная не может быть сколь угодно большой, а система, по крайней мере, в настоящем виде приводит к неограниченному возрастанию импульса и значений, то необходимо изменить структуру системы. Проводя в жизнь стратегию “обращения структуры расценок” получим систему устойчивую импульсно, но не абсолютно. Это означает, что, несмотря на наличие внутренних ограничений на размер импульса в системе, она не является сбалансированной и саморегулирующейся, поскольку значения параметров в ее вершинах могут изменяться неограниченно. Если в дополнение к обращению структуры расценок проводить политику вытеснения старых предприятий при строительстве новых электростанций, можно теоретически получить систему, абсолютно устойчивую для всех простых импульсных процессов. На практике предусмотреть подобный комплекс мер, конечно, сложно. Кроме того, это всего лишь одна из стабилизирующих стратегий. Возможно, существуют более простые способы достижения этой же цели. Ответ на этот вопрос можно получить, используя второй подход к формированию стратегий. Он основывается на особенностях структуры СЭС и применим только для графов топологии обобщенная роза. База этого подхода – теоремы о зависимости между лепестковой последовательностью знаковой розы и ее устойчивостью (лабораторная работа №1 теоремы 8, 9). Т.4. Пусть D – обобщенная знаковая роза с лепестковой последовательностью <a1,a2,...as>, s>0. Если D импульсно устойчив для всех простых импульсных процессов, то
Т.5. Пусть орграф D – обобщенная знаковая роза с лепестковой последовательностью Однако делать вывод об импульсной устойчивости, основываясь на теореме 4 нельзя, так как она дает необходимое, но не достаточное условие. Свойство импульсной устойчивости необходимо проверить, используя другие методы, например, теорему 4. Это несложно сделать, учитывая, что характеристический многочлен обобщенной розы определяется по формуле:
где n – число вершин в орграфе. Представляющий описываемую систему (см. рис. 3.1.) орграф – обобщенная роза с центральной вершиной U. В нем есть один контур длины 2, три контура длины 3 и один – длины 5. Для любых знаков имеем: Необходимыми условиями импульсной и абсолютной устойчивости являются:
Первое выражение в нашем случае верно всегда. Второе – для i = 1 и i = 4. Для i=2, 3 оно может быть записано Так как Следовательно, систему можно переписать в виде:
В рассматриваемом ОЗ эти условия не выполняются. Чтобы получить Требуемую лепестковую последовательность можно получить, изменяя не 2, а 3 и более дуг, но, учитывая, что за каждым таким изменением стоит конкретная проблема преобразований в экономической и социальной сфере, остановимся на рассмотрении выше найденных вариантов. Тем более, что оптимальная стабилизирующая стратегия должна быть наиболее простой в исполнении. Этап 6. Выбор и обоснование оптимальной стратегии. На предыдущем этапе формальными методами были получены следующие возможные стратегии: Заменить знак дуг Все эти стратегии приведут, в конечном счете, к структуре графа, характеристический многочлен которого равен:
Его собственные значения не являются кратными (за исключением нулевых) и не превышают по модулю единицу. Следовательно, эти стратегии действительно стабилизирующие. Первая стратегия уже была подробно рассмотрена. Вторая и третья стратегии требуют введения механизма, обеспечивающего прямую зависимость между стоимостью электроэнергии и ее потреблением, что с экономической точки зрения является абсурдным. Кроме того, весьма проблематично увеличивать число рабочих мест при сокращении количества предприятий или влиять на населенность города антиэкономическими методами. Т.о. последние две стратегии являются стабилизирующими лишь чисто теоретически, и не могут быть осуществлены на практике. Следовательно, простейшая оптимальная стратегия управления данной системой заключается в применении политики, секвестирующей некоторые отрасли при строительстве новых электростанций, органично сочетаемой с обращением структуры расценок в энергосистеме.
|






 R Q
R Q – +
– +




 C U P
C U P + +
+ +

 F + J
F + J




 i = 1, 2, …, s-1
i = 1, 2, …, s-1 и D импульсно устойчив для всех простых импульсных процессов, тогда D абсолютно устойчив для всех простых импульсных процессов тогда и только тогда, когда
и D импульсно устойчив для всех простых импульсных процессов, тогда D абсолютно устойчив для всех простых импульсных процессов тогда и только тогда, когда  .
. ,
,

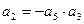 .
. , то
, то  .
. единственный набор, удовлетворяющий ей
единственный набор, удовлетворяющий ей 

 , необходимо изменить знак дуги (U,R) либо (R,U). Если был изменен знак дуги (R,U), то мы можем получить
, необходимо изменить знак дуги (U,R) либо (R,U). Если был изменен знак дуги (R,U), то мы можем получить  , изменяя знак одной из дуг (F,J) или (J,P). Никакие другие изменения одной единственной дуги не приведут к требуемому результату. Если был изменен знак дуги (U,R), то для получения устойчивой структуры следует изменить знак дуги (C,F).
, изменяя знак одной из дуг (F,J) или (J,P). Никакие другие изменения одной единственной дуги не приведут к требуемому результату. Если был изменен знак дуги (U,R), то для получения устойчивой структуры следует изменить знак дуги (C,F). на противоположный.
на противоположный. 



