ТЕОРИЯ БЛАГОСОСТОЯНИЯ

13. Потребительский излишек

Если бы было можно измерять предельную полезность денежного дохода каким-ни­будь методом вроде того, что был предложен Нейманом и Моргенштерном, то можно было бы получить функцию предельной полезности отдельного товара для данного потребителя, исходя из его функции потребления, с помощью формулы равновесия: MU_x = P_xMU_e. Но даже в отсутствие количественного способа измерения MU_e мы можем сказать, что предельная полезность ''второстепенного'' товара равна его цене при условии постоянной величины MU_e. При малых колебаниях реального дохода мы можем предположить, что добавление одного доллара к общим расходам потребителя увеличит его совокупную полезность на постоянную величину. Поэтому цена, кото­рую потребитель готов уплатить за данное количество товара х, прямо выражает для него предельную полезность x. Равным образом совокупная полезность приобретения определенного количествах, учитывая, что x занимает второстепенное место в бюдже­те потребителя, может быть получена путем суммирования предельных полезносгей, связанных с последовательными приращениями x от точки О до С (рис. 9-12). Посколь­ку каждый тоненький параллелограмм выражает предельную полезность каждого конечного приращениях, общая полезность всего количества от О до С равна О ABC. Потребитель был бы готов уплатить всю сумму ОАВС, но фактически он заплатит за ОС сумму, равную ОЕВС. Следовательно, ЕАВ равен потребительскому излишку от покупки ОС товарах; этот же треугольник измеряет величину потери благосостояния потребителя, если бы ему помешали приобрести какое-либо количество товара х. Этот излишек на самом деле есть излишек полезности, но его можно выразить и в денежной форме благодаря нашей неизменной единице измерения, а именно предельной полез­ности расходов вообще*.

* Предельная полезность денежного дохода — не единственная неизменная величина, которую можно было бы использовать. Уикстид в своей книге "Alphabet of Economic Science* (1889) предложил использо­вать "данное количество труда в качестве стандартной единицы для оценки величины удовлетворения потребностей. К примеру, полезность определенного количества тонн угля можно выразить величиной труда, который индивид готов затратить на подъем 100 тонн какого-либо другого груза". "В академиче­ских кругах, — замечал Уикстид, — принято считать 1 час, затрачиваемый на проверку экзаменацион­ных работ, стандартной мерой удовольствий и страданий". Однако, несмотря на эти убедительные примеры, все же нет оснований полагать, что теорию благосостояния можно поставить на твердую основу с помощью определения неизменной единицы тягости труда в духе Адама Смита [см. гл. 2, раздел 10].

Маршалл определил этот род потребительского излишка как "излишек сверх цены, уплачиваемой потребителем в действительности, который он скорее уплатит, чем останется без данной вещи". Мы можем рассматривать его и в духе Дюпюи [см. гл. 8, раздел 16] как ту величину, которую можно изъять у потребителя благодаря ценовой дискриминации. Если бы монополист смог постепенно сдвигать свою цену вдоль кривой потребительского спроса, его предельный доход был бы равен цене последней проданной единицы товара, поскольку он всегда может продать добавочную единицу по более низкой цене без понижения цены всех прочих единиц. Максимально возмож­ный доход от такого рода дискриминации и есть "ценовой излишек", по Дюпюи, являющийся денежным измерителем избытка полезности для потребителя, возника­ющего от того, что последний может покупать каждую единицу товара по одной и той же цене. Математически излишек измеряется как площадь под кривой спроса от нуля до данного количества минус прямоугольник со сторонами, равными равновесной цене и равновесному количеству.

Нам приходится исходить из предпосылки, что кривая спроса пересекает ось цен. Если же индивидуальная цена спроса в отношении первой единицы не определена и кривая спроса не касается оси у, интеграл под кривой спроса будет бесконечным. Но это возражение легко преодолеть, измеряя потребительский излишек, начиная с не­которой положительной величины на оси x. Существует и более серьезное возражение против измерения потребительского излишка в виде треугольника, расположенного под кривой спроса. Если мы предположим, что индивид, имея данный доход, будет закупать последовательные единицы товарах по той максимальной цене, которую он готов уплатить за каждую единицу, то мы получим кривую спроса при постоянном доходе, т.е. кривую спроса Фридмена—Маршалла, или "кривую предельной оценки", как назвал ее Хикс, которая всегда располагается ниже кривой спроса Маршалла при более низких ценах и выше ее при более высоких ценах. Это объясняется тем, что реальный доход, если цена падает, возрастает вдоль маршалловской кривой спроса, а при более низких ценах кривая спроса при постоянном реальном доходе сдвигается, как ей и положено, вправо; точки пересечения сдвигающейся кривой спроса при постоянном реальном доходе с чередующимися горизонтальными линиями цен обра­зуют маршалловскую кривую спроса (см. рис. 9-13). Если начальная цена равна р₂, то кривой предельной оценки будет т₂, если начальная цена — p₁, тогда кривой предель­ной оценки станет m₁и т.д. Недвусмысленная оценка потребительского излишка может быть получена только на основе кривой, аналогичной кривой предельной оценки, которая предполагает постоянство реального дохода, и показывает все куп­ленные единицы по отдельности по их полным предельным ценам. Для данного

количества купленных товаров х маршалловская кривая спроса завышает величину потребительского излишка.

Частично в результате признания этого возражения Маршалл на практике стал измерять потребительский излишек при данном изменении цены.

Во всех случаях, когда концепция потребительского излишка находила действи­тельное применение, Маршалл использовал исключительно участок нормальных из­менений цен, определяя потребительский избыток на основе изменения цены как площадь между кривой спроса и осью цен в пределах данного изменения цены. Вслед за Хиксом мы будем называть это "маршалловской мерой". В той мере, в какой мы рассматриваем лишь малые изменения потребленных количеств "второстепенных" товаров, кривая предельной оценки практически сливается с кривой спроса, и психо­логические оценки выигрыша или потери для потребителя вследствие малого измене­ния цены могут быть прочитаны непосредственно с помощью кривой спроса. Это значит, что реально мы можем применить маршалловскую концепцию потребитель­ского избытка для измерения удовлетворения, получаемого от возможности покупки данного количества товара х по цене ниже той, которую индивид готов был бы упла­тить, только бы не остаться вовсе без этого товара. Правда, данное понятие излишка остается полезным для демонстрации того факта, что цена, уплачиваемая за предмет, не является мерой приносимого им удовлетворения, но мы не можем измерять этот избыток более или менее приемлемым образом. В лучшем случае мы можем оценить эффект благосостояния, сравнивая одну комбинацию цены и количества с другой при условии, что расходы на рассматриваемый товар составляют малую часть общих расходов.

14. Формальное изложение

Трудности измерения потребительского излишка на базе кривой спроса можно про­иллюстрировать посредством кривых безразличия. Если мы будем отмечать количе­ство денег на вертикальной оси, а товара х — на горизонтальной (см. рис. 9-14), маршалловская предпосылка постоянной предельной полезности денег будет соответ­ствовать кривым безразличия, изображаемым параллельными вертикалями: при лю­бом данном количестве х наклон кривых, выражающих предельную норму замещения между деньгами и товаром х, или MU_x /MU_e, остается тем же самым независимо от того, какое количество денег мы откладываем по ординате. MRS (предельная норма заме­щения) зависит только от объема потребления, а не от количества денег, истраченного на товары в целом. Денежные расходы индивида настолько велики, что малые изме­нения в объеме его расходов не влияют на его готовность расставаться с денежными средствами, или, говоря иначе, даже если величинах постоянна, при снижении MU_e по мере роста количества денег MU_x, тоже снижается, поскольку деньги и x — конкури-

рующие товары. По любой причине, если мы двигаемся вдоль вертикальной линии, MRS остается постоянной, поскольку оба показателя — MU_x и MU_e, изменяются в одинаковой пропорции. В результате при любом данном количестве* MRS на каждой кривой безразличия равняется рх; система кривых безразличия сводится к единой кривой MRS, а это и есть кривая спроса (см. рис, 9-14). Предположим, индивид нахо­дится в точке R, имея данное количество денежного дохода ОМ; при ценовой структу­ре, характеризующейся MOQ, он покупает O_ql товара x, расходуя R_ql на другие товары и TR — на товар x. Цена x = TR/MT = OM/OQ. Поскольку наклоны кривых безразли­чия в точках S, R и Т одинаковы и равны наклону линии цены MQ, MRS всех кривых безразличия при количестве O_ql равны p₁); на пространстве, характеризующем соотно­шение цены и количества. При более низкой цене x, изображаемой линией цены ML, индивид сдвигается в точку R'; используя те же рассуждения, получим OM/OL - р₂.

Таким способом вся кривая спроса на товар х может быть выведена из карты кривых безразличия.

Маршалловский "ценовой излишек" соответствует максимальной сумме, которую потребитель готов затратить, имея перед собой выбор — либо товар х, либо ничего. Пусть потребитель находится в исходной ситуации, в точке R.

Тогда максимальная сумма, которую он предложит, чтобы не остаться без товара х, равна TS, поскольку для него безразлично, израсходовать TS или лишиться x — одно не хуже другого. Это возвращает его на кривую безразличия 1, с которой он начинал, имея данный денежный доход М и до того, как х был предложен ему по цене p₁ · RS = ММ' измеряет "излишек" сверх цены, возникающий благодаря тому, что вы можете купить O_ql товаров х по единой цене p₁;, а это в точности равно площади p₁Ar, располо­женной под кривой спроса над прямоугольником расходов. Это вытекает из того факта, что полученная нами кривая спроса на самом деле есть кривая спроса при постоянном реальном доходе, вычерченная исходя из предпосылки, что предельная полезность денежного дохода строго постоянна. Равным образом, если цена падает до уровня pi, новый "ценовой излишек" будет равен R'k, а это в точности равно площади piAk под кривой спроса; выигрыш в величине потребительского излишка от падения цены, таким образом, равен заштрихованной площади p₂p₁rk, расположенной под кривой спроса.

Предположим, теперь мы откажемся от предпосылки постоянства предельной полезности денег и допустим, что MRS увеличивается по мере роста величины денеж­ного дохода. Двигаясь вверх по вдоль вертикали, мы последовательно пересекаем кривые безразличия со все более крутым наклоном. Это тот случай, когда эластич­ность спроса на товар х по доходу положительна: параллельные сдвиги бюджетных линий увеличивают требуемое количество х. Следовательно, эта система кривых безразличия более несводима к единой кривой MRS. Каждая кривая безразличия имеет отныне свою собственную кривую MRS (см. рис. 9-15). К примеру, на линии цен MQ объем купленного товара составит О_ql. Пунктирные линии т_1,2,3 — это кривые MRS, соответствующие кривым безразличия 1,2 и 3 для количества О_ql товарах. Они расположены одна над другой, поскольку наклон последовательных кривых безраз­личия для данного количества товара х повышается вместе с растущей величиной денежного дохода. Кривые MRS были изображены в виде параллельных прямых линий для удобства. Так, р₂ — это цена, при которой будет куплено O_ql товара x, она равна наклону кривой безразличия 2 в точке R. Равным образом цена р₁ на кривой MRS "m₃", представляет собой наклон кривой безразличия 3 в точке R' и является той ценой, по которой будет закуплено Oq₂ товара х. Связав эти точки, мы выделим кривую спроса, которая на этот раз будет иметь более пологий наклон, чем любая из кривых MRS. Очевидно, что если бы эластичность спроса по доходу была отрицательной, а кривые безразличия сближались бы с левой, а не с правой стороны, то последователь­ные кривые MRS располагались бы друг под другом, а кривая спроса была бы более крутой, нежели любая из кривых MRS.

Потребительский "излишек сверх цены" в этом более общем случае не равен треугольнику под кривой спроса. Например, "потребительский излишек" для количе­ства Oq₁ равен RK, или ТК — RТ, Величине ТК соответствует максимальная сумма, которую потребитель готов истратить, чтобы не остаться вовсе без товара х, — она изображается площадью Ор₃sq₁ под кривой MRS "m₁"; величине Rt cooтветствует здесь площадь прямоугольника, сторонами которого являются цена и количество, — Op₂rq₁ под кривой спроса. Вычитая последнюю величину из первой, мы получаем заштрихо­ванный треугольник р₂p₃d минус заштрихованный треугольник drs. Это явно меньше, чем треугольник р₂p₃r, расположенный под кривой спроса. Мы получили тот же ре­зультат, что и прежде: маршалловский "ценовой излишек" завышает размеры потре­бительского излишка, способного образоваться при закупке всех товаров по единой цене. Он завышает этот излишек вследствие положительного эффекта реального дохода. Повторяю еще раз: очевидно, что если эластичность спроса на товар MRS по доходу была бы отрицательной — если бы MRS уменьшалась с ростом величины

денежного дохода, то треугольник, расположенный под кривой спроса, оказался бы меньше этого излишка.

15. Четыре вида потребительского излишка

Эти выводы могут быть применимы и к измерению роста или падения потребитель­ского излишка при изменении цены. Мы знаем, что кривая спроса при постоянном реальном доходе всегда располагается под маршалловской кривой спроса при более

низких ценах и над ней — при более высоких. Если мы станем пользоваться кривой спроса, чтобы выяснить величину прироста или уменьшения потребительского из­лишка, то мы завысим величину выигрыша при сокращении цены и недооценим величину потери при ее повышении. Поэтому мы располагаем двумя видами денеж­ного измерения этой величины при данном ценовом изменении: 1) компенсационной выплатой, которая сохранит индивиду прежнее материальное положение, если ему не позволено будет вернуться к первоначальному состоянию; 2) компенсационной вы­платой, которая сохранит потребителю прежнее положение, если ему будет обеспечен возврат к первоначальному состоянию путем "перезаключения контракта". Кроме того, мы имеем еще два способа денежного измерения в зависимости от того, учиты­ваем мы или нет эффект дохода. В результате мы получаем полный обзор хиксовских "четырех видов потребительского излишка".

Возьмем случай, когда р_х снижается и индивид переходит из точки R в точку R' (рис. 9-16). Тогда мы имеем в порядке возрастания:

1) величину, характеризующую количественную компенсацию, — R'r'. Когда

цена снижается, потребитель переходит на кривую безразличия 2, покупая Оq товарах и R'q прочих вещей. Если ему не обеспечено "перезаключение контракта", R'r' может быть у него изъято, для того чтобы его положение осталось прежним;

2) величину, характеризующую ценовую компенсацию, — R'R'₁. Фактически

положение потребителя улучшилось бы, если бы он утратил R'r', потому что линия цены, проходящая чере r ', была бы касательной к более высокой кривой безразличия, нежели кривая 1. Сумму, равную R'R'₁, пришлось бы у него вычесть, чтобы компенсировать первоначальный прирост реального дохода вследствие падения цены, если допускается "перезаключение контракта". Разницы между п. 1 и 2 не существует, если кривые безразли­чия представляют собой параллельные вертикали;

3) величину, характеризующую ценовую эквивалентность,— RR₁. Если потре-

битель вынужден был еще раз платить более высокую цену, но ему дозво­лялось, "перезаключив контракт", вернуться в точку R, тогда RR₁ будет означать рост денежного дохода, компенсирующий предстоящее сокраще­ние p.

4) величину, характеризующую количественную эквивалентность, —- Rr. Слу-

чай 3 передвинет индивида на кривую безразличия, расположенную ниже

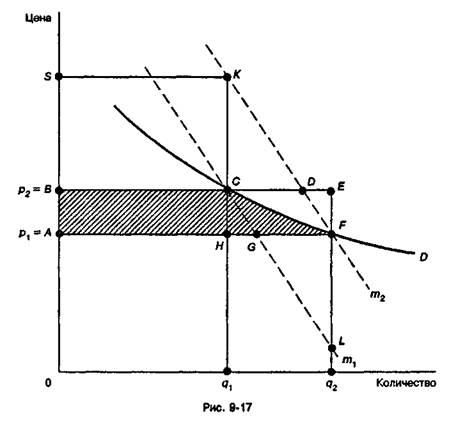
кривой Rr, — это мера полного прироста реального дохода вследствие падения p_x. Разница между 3 н 4, как и между случаями 1 и 2, исчезает, если кривые безразличия представляют собой параллельные вертикали.

Какой из четырех способов измерения соответствует "маршалловской мере" — заштрихованной площади между кривой спроса и осью цены в рамках данного изме­нения цены (см. рис. 9-17)? Если говорить точно, то ни один из них. Если первоначаль­ная цена р₂ = ОВ падает до уровня; p₁ = ОА, кривая МRS "m₁"для постоянного реального дохода будет иметь такой же вид, как и для р_2. В этом случае величина, характеризу­ющая количественную компенсацию, — (1) будет равна ABCG минус GFL₁ или OBCLq₂, т.е. тому, что индивид был бы готов уплатить за q₂ , дабы сохранить свое прежнее положение, минус величина OAFq₂ — иными словами, тому, что он платит на самом деле. Положение индивида не улучшилось бы от того, если бы он вынужден был купить дополнительное количество q₁q₂ по цене р₂q₂, но оно ухудшилось бы, если бы он смог закупить все q₂ по цене р₁. Следовательно, величина, характеризующая ценовую компенсацию (2), — это ABCG. Итак, два компенсационных платежа (1) и (2) оказываются меньше "маршалловской меры". С другой стороны, две величины, характеризующие эквивалентность, — (3) и (4), превышают "маршалловскую меру". Если m₂предполагает такой же постоянный реальный доход, как и p₁, то величина, характеризующая ценовую эквивалентность (3), оцененную для меньшего количест­ва q₁, равна площади ABDF — по аналогии с вариантом, характеризующим ценовую компенсацию. Равным образом величина, характеризующая количественную экви­валентность (4), равна площади ABDF плюс CKD: чтобы находиться на линии т₂ и купить q₁ цена должна подняться до уровня S, и в этом случае общая потеря потреби­тельского излишка составила бы АВSКDSF; фактически же величина BSKC не опла­чена, так что мы остаемся с величиной ABDF плюс CKD. В итоге эти две величины,

характеризующие эквивалентность, больше, чем "маршалловская мера", изображае­мая заштрихованной площадью.

Следует отметить, что выгоды и потери, измеренные в единицах полезности, одинаковы как при повышении цены, так и при эквивалентном ее снижении, но потребительский избыток, измеренный в деньгах, будет разным, поскольку в этих двух случаях разной будет ценность денег, выраженная в товарах. Фактически при повышении цены величины, характеризующие компенсацию, — (1) и (2) становятся величинами, характеризующими эквивалентность, — (3) и (4), и наоборот.

16. Анализ налогов и субсидий

Истощив терпение на тонкостях оценивания потребительских излишков на основе кривой спроса, мы должны теперь рассмотреть следующую ситуацию: если доля расходов, предназначенных на данный товар, мала и если кривая спроса на отрезке между двумя изменениями цен в высшей степени эластична, тогда все четыре вида потребительского излишка сливаются и становятся равными "маршалловской мере". Предположив, что это так, мы еще не показали, каким образом в рыночных условиях можно складывать индивидуальные потребительские излишки, чтобы получить меру совокупного потребительского излишка, возникающего вследствие изменения цены. Когда Маршалл использовал это понятие на практике, он всегда употреблял множе­ственное число — "потребительские излишки": его интересовала в первую очередь коллективная выгода всех покупателей. Он начинает с индивидуального излишка, а затем применяет следующую аргументацию: большинство рынков однородны в том смысле, что покупатели обладают примерно равными доходами. Это оправдывает предположение, согласно которому индивид является модальным представителем группы. Таким способом Маршалл решает проблему аддитивности, избегая вопроса о том, как совокупный избыток распределяется между индивидуальными покупателя­ми. Очевидно, что эффекты Веблена, при которых в каждой индивидуальной функции полезности появляются полезности или доходы других людей, разрушают возмож­ность агрегирования потребительских излишков. Даже при наличии аддитивных фун­кций полезности концепция потребительских излишков требует от нас межличност­ных сопоставлений.

Постоянное использование Маршаллом этой концепции при анализе налогов и субсидий дает превосходный пример той беззаботности, с которой большинство эко­номистов-неоклассиков делали свои выводы в отношении теории благосостояния. Маршалл начинает с показа того, что налог на товар, производство которого подчиня­ется закону постоянной отдачи или постоянных издержек, приводит к потере потре­бительских излишков, которые превышают величину налоговых поступлений, и нао­борот, субсидии на приобретение такого товара превышают выгоды от потребитель­ских излишков. Объединим на графике кривую спроса с горизонтальной долгосрочной кривой предложения (см. рис. 9-18) и введем единый налог LA на каждую единицу покупаемого продукта. Кривая предложения сдвигается вверх на величину налога, так что потеря потребительского излишка выражается площадью SsRA под кривой спроса. Налоговые поступления равны SsRK. Разница показана заштрихованным треугольником. Равным образом, если субсидия сдвигает долгосрочную кривую пред­ложения вниз, с уровня ss до SS, треугольник RAL над кривой спроса будет представ­лять превышение выплачиваемых субсидий над приростом потребительского излиш­ка.

В случае отрасли, работающей в условиях убывающей отдачи, субсидия дает тот же результат. Чтобы преодолеть силы, стимулирующие рост издержек, субсидия дол­жна пропорционально увеличиваться; и вновь субсидия превышает прирост потреби­тельского излишка вследствие снижения цены. Воздействие же налога в данном случае менее определенно. Здесь налоговые поступления составляют BARK, а умень­шение потребительского излишка — CARD (рис. 9-19). Поскольку заштрихованный треугольник BCLK превышает заштрихованный треугольник RDL, налоговые поступ-

ления превышают потерю потребительского излишка — результат, противополож­ный тому, что мы получили ранее. Ясно, что этот вывод зависит от степени крутизны долгосрочной кривой предложения, т.е. от интенсивности воздействия факторов, вли­яющих на снижение отдачи.

При растущей отдаче или снижающихся издержках долгосрочная кривая предло­жения имеет понижательную траекторию. В этом случае потеря потребительского излишка вновь должна превзойти налоговые поступления. Налогообложение отрасли

со снижающимися издержками повышает цены и тем самым увеличивает потери потребительского излишка сверх налоговых поступлений. Воздействие же субсидии зависит исключительно от наклона кривой предложения (см. рис. 9-20). Величина субсидии равна TFER, а прирост потребительского излишка — TCAR. Как показано на графике, заштрихованная трапеция больше заштрихованного треугольника: сле­довательно, прирост потребительского излишка превышает величину субсидии. Но если кривая предложения была бы более эластичной, мы получили бы случай посто­янных издержек: тогда субсидии превышали бы величину потребительского излишка.

Вся эта аргументация может быть сведена воедино на основе предположения, согласно которому отрасль с растущими издержками и отрасль с падающими издерж­ками сталкиваются с одной и той же кривой спроса (см. рис. 9-21).

Первоначально отрасль с растущими издержками производит величину продук­ции Оq₂, а отрасль со снижающимися издержками — Oq₁. Первая отрасль облагается налогом, а затем налоговые поступления используются для субсидирования второй отрасли, т.е. прямоугольник KAFQ равен прямоугольнику CLHD. Чистый прирост потребительского излишка показан с помощью заштрихованной площади CBED. От­расль с растущими издержками теперь производит Oq₁, а отрасль со снижающимися издержками — Oq₂ чистый прирост физического выпуска равен q₂q₃. Какой вывод можно сделать из этого? По-видимому, государство может увеличить совокупное экономическое благосостояние, облагая налогом отрасли с растущими издержками в том случае, если налоговые поступления способны превысить возникающее уменьше­ние потребительского излишка, и используя поступления в целях субсидирования отраслей со снижающимися издержками, в которых субсидии могут быть меньше, чем конечный прирост потребительского излишка. Эта аргументация зависит от возмож­ности разграничения отраслей с возрастающими и со снижающимися издержками, что само по себе, как мы увидим, составляет изрядную проблему. Кроме того, факторы, обусловливающие рост или снижение издержек, в каждой группе отраслей должны действовать весьма отчетливо. Маршалловское доказательство носит чисто геометри­ческий характер, но обоснование, лежащее в его основе, на самом деле очень простое. Налог на отрасли с растущими издержками увеличивает их цену предложения и

снижает величину предложения; это позволяет производить товары при более низких издержках, соответствующих более эффективному использованию ресурсов. Цена предложения растет, но в меньшей степени, чем налог, благодаря экономии, возника­ющей вследствие производства предельной единицы при более низких издержках. Затем налоговые поступления используются для субсидирования отраслей со снижа­ющимися издержками; цены в этих отраслях падают по мере роста выпуска продук­ции, поскольку возросшее количество производится с более низкими издержками на единицу продукции. Общее удовлетворение в целом возросло, поскольку ресурсы переместились от производства товаров с растущими ценами предложения к товарам, производимым при падающих ценах предложения.

Маршалл проявлял некоторую осторожность относительно практической приме­нимости этой части своей теории. Он предупреждал о наличии административных проблем, связанных со сбором налогов и определением уровня субсидий. Однако этот аргумент играет важную роль в его критике вульгарного "учения о гармонии" (Harmonielehre) — доктрины, согласно которой совершенная конкуренция непремен­но максимизирует удовлетворение всех потребностей общества. Эта доктрина, утвер­ждал он, не только не требует абсолютно равного распределения дохода, он и предпо­лагает, что все отрасли работают в условиях постоянных издержек. Если последнее не выполняется, совокупное удовлетворение может быть всегда увеличено путем стиму­лирования производства в отраслях со снижающимися издержками за счет отраслей с растущими издержками. В этом смысле анализ налогов и субсидий, по крайней мере, способствует опровержению "доктрины максимального удовлетворения потребно­стей".

Описанная нами аргументация следует прямо из текста Маршалла. Очевидно, однако, что она неполна, поскольку не учитывает изменение в величине излишка, получаемого не только потребителем, но и производителем в результате налога или субсидии. Маршалл касается проблемы производительского излишка в Приложении Н своих "Принципов", но допускает здесь определенную путаницу. Эта путаница вызвана неясной концепцией убывающей долгосрочной кривой предложения. Но прежде чем мы сможем плодотворно рассмотреть этот вопрос, необходимо сделать

общий обзор маршалловской теории ценообразования для короткого и длительного периодов времени.

РЕКОМЕНДАЦИИ К ДАЛЬНЕЙШЕМУ ЧТЕНИЮ

В моей трактовке концепции измеримости полезности я опирался на статьи А.А. Alchian "The Meaning of Utility Measurement* (AER, 1953, перепечатано в EMDT); D. Ellsberg "Classic and Current Notions of Measurable Utility* (EJ, 1954, перепечатано в RHETanu UT) и W.J. Baumol "The Cardinal Utility Which is ОпЧпаГ (EJ. December 1958), воспроизведено в Economic Theory and Operations Analysis (4th edn., 1977, в бумаж­ном переплете), chap. 17, живо написанная монография: Т. Majumdar "The Measure­ment of Utility* (1958), содержит дополнительные соображения.

По истории теории полезности см. GJ. Stigler "The Development of Utility Theory* (JPE, 1950), перепечатано в ЕЕТапй UT, а также в его 'Essays in the History of Economics*.

В этой книге помещена его захватывающе интересная статья, состоящая из двух частей, в которой дается обзор всей литературы вплоть до 1914 г., включая некоторые интересные замечания о том, чем характеризуются "успешные" теории. D.N. Rosentein-Rodan 'Marginal Utility* (1972), перепечатано в IEP, N.10, 1960, дает отличную картину доктрины предельной полезности, сложившуюся в Европе к пе­риоду первой мировой войны, во всем разнообразии отдельных концепций, выделя­емых на основе метафизической классификации и тончайших различий. Читая этот очерк, понимаешь, как много было отброшено в этой теории революцией, произве­денной Хиксом и Алленом, и, как нам кажется, к лучшему.

A.R. Sweezy *The Interpretation of Subjective Value Theory in the Writings of the Austrian Economists* (REStud. June 1934).

В этой работе Суизи считает, что австрийские экономисты молодого поколения в 20-х годах независимо от других приближались к ординалистской концепции полез­ности.

Работа Бернулли 1738 г. о Санкт-Петербургском парадоксе перепечатана в "С/Г and Precursors in Mathematical Economics*, eds. Baumol and Goldfeld. Там же перепеча­тана пророческая статья: W.E. Johnson's "Ttie Pure Theory of Utility Curves* (1913). Гораздо более известную статью Слуцкого (1915), впервые по-настоящему разделив­шего эффект замещения и эффект дохода, порождаемые изменением цен, можно прочитать в "Readings in Price Theory", eds. GJ. Stigler and K.E. Boulding (1953). PA Samuelson 'St. Petersburg Paradoxes: Defanged, Dissected, and Historically Described", JEL, March 1977, рассматривает Санкт-Петербургский парадокс в историческом кон­тексте.

E.D. Pagan 'Recent, and Contemporary Theories of Progressive Taxation" (JPE. 1938*), reprinted in "Readings in the Economics of Taxation", eds. Musgrave and Shoup, дает обзор исторического развития теории прогрессивного налогообложения в традициях теории полезности. На ту же тему см. подробный обзор в книге Musgrave "Theory of Public Finance", chap. 5. J. Viner "The Utility Concept in Value and Its Critics" (JPE, 1925), перепе­чатано UT и в его книге 'The Long View and the Short", анализирует традиционные направления критики теории полезности. Первая из этих статей, касающаяся роли полезности в теории спроса, сегодня так же актуальна, как и в 1925 г.; вторая, имеющая дело с теорией благосостояния, несколько устарела.

F.H. Knight "Realism and Relevance in the Theory of Demand" (JPE, 1944), перепечатана в EMDT, доказывает, что подход с точки зрения кривых безразличия фактически предполагает снижающуюся предельную полезность и не представляет собой сущест­венного прогресса по сравнению со старой теорией полезности. Его справедливо кри­тикует за это R.L. Bishop "Professor Knight and the Theory of Demand" (JPE. April 1946). См. также Schumpeter "History of Economic Analysis", pp. 1054—1073.

GJ. Stigler 'The Earfy History of Empirical Studies of Consumer Behavior* (JPE, 1954), перепечатано в его "Essays in the History of Economics", рассматривает начало эмпири-

ческого анализа функции спроса от дохода и кривых спроса; что касается последнего, то ничего серьезного не предпринималось вплоть до первой мировой войны.

К. A. Fox 'Demand and Supppfy: Econometric Studies" (/£55,4) дает сжатое изложение истории эмпирических исследований по проблеме спроса после 1900 г. В "Notes on the History of the Giffen Paradox" (JPE. April 1947; "Comment* by A.R. Prest, Ibid., February 1948) Stigler показывает, что Маршалл интерпретирует положительный наклон кри­вой спроса на хлеб "в стиле" Гиффена; данные же самого Гиффена относительно потребления хлеба не обнаруживают этого парадокса. Для переоценки доказательст­ва Стиглера см. W.P. Gramm "Giffen's Paradox and the Marshallian Demand Curve" (MS. March 1970) и S. Kashid "The Beeke Good: A Note on the Origins of the "Giffen Good" (HOPE. Winter 1979).

M. Friedman "The Marshallian Demand Curve" (JPE, 1949), перепечатано в EMDT, AMCA, III, и его "Essays in Positive Economics" (1953, в бумажном переплете) утвержда­ет, что кривые спроса должны определяться при постоянном реальном доходе и что подобная интерпретация ближе всего соответствует тому, что в действительности имел в виду Маршалл; приложение к "Эссе" Фридмена содержит подробный коммен­тарий соответствующих разделов "Принципов". R.F.G. Alford "Marshall's Demand Curve" (Ее., 1956), перепечатано в AMCA, III, отвергает фридменовскую интерпрета­цию и восстанавливает традиционную позицию; в учебных целях мы настоятельно рекомендуем эту статью. См. в том же плане W.J. Fellner "Emergence and Content of Modem Economic Analysis" (I960), chap. 14 and 15. L. Yeager "Methodenstreit over Demand Curves" (JPE, 1960), перепечатано в EMDT, поднимает вопрос о методологической основе интерпретации Фридмена. E.J. Mishan "Theories of Consumer's Behaviour: A Cynical View" (Ec., 1963), перепечатано в EMDT, пытается убедить читателя, что все нынешние теории потребительского поведения не стоят тех трудов, которые необхо­димы, чтобы разобраться в них, и что начинающему экономисту будет вполне доста­точно принять "закон спроса" на веру. J.P. Henderson "William Whewett's Mathematical Statements of Price Flexibility, Demand Elasticity and the Giffen Paradox" (MS. September 1973) показывает, что за сорок пять лет до Маршалла и за девять лет до Курно Уивелл придумал и записал показатель, обратный ценовой эластичности спроса, и открыл способы идентификации гиффеновских товаров. D.A. Walker "Marshall's Theory of Competitive Exchange" (CJE, 1969), перепечатано ъАМСА, III, объясняет, каким образом предпосылка постоянства MU, для каждого торговца на рынке позволила Маршаллу обойти проблему неравновесных сделок.

Что именно Маршалл предполагал считать постоянным — денежный запас или денежный поток? Этот вопрос продолжает оставаться центром разногласий его ком­ментаторов: см. Н.Н. Liebhafsky "Marshall and Slutsky on the Theory of Demand" (CJE, 1961); R.A. Bilas "Liebhafsky and the Constant Marginal Utility of the Numeraire: A Comment" (Ibid., 1965); G. Higgins H.H. Liebhafsky "Pareto and the Marshallian Constancy Assumption" (SES, 1968); N. Georgescu-Roegen "Revisiting Marshall's Constancy of Marginal Utility of Money" (Ibid., 1968), все перепечатано ъАМСА, III, R.B. Ekelund, Jr., E.G. Furubotn, and W.P. Gramm, EMDT, хрестоматия, на которую мы часто ссылались, включает также сгостраничную монографию по эволюции теории спроса, ее вторая глава посвящена теории спроса маршаллианского направления. Истории интерпретаций теории спроса Маршалла, видимо, не будет конца: пример недавнего и неожиданно нового осмысле­ния дает работа Т. Biswas "The Marshallian Consumer" (Ec. February 1977). R.L. Bishop "Consumer's Surplus and Cardinal Utility* (QJE. May 1943), содержит блестящее рассмот­рение трудностей маршаллианской концепции, включая старые возражения, выдви­нутые Никольсоном и Кэннаном, маршаллианский анализ излишка рассматривается в работе Myint "Theories of Welfare Economics", chap. 9; см. также гл. 8 его книги "Characteristic of Neo-classical Welfare Economics";.

Перевод проблемы на язык кривых безразличия см J.R. Hicks "The Four Consumer's Surpluses" (REStud. Winter 1943) и K.E. Boulding "The Concept of Economic Surplus" (AER, 1945), перепечатано в "Readings in the Theory of Income Distribution", eds. W. Fellner and B.F. Haley (1946). J.N. Morgan "The Measurement of Gains and Josses" (QJE. February 1948)

цитирует и обозревает всю последнюю литературу по проблеме потребительского излишка и предлагает практические методы его измерения. АР. Lerner "Con