Измеримость полезности

ТЕОРИЯ ПОЛЕЗНОСТИ

Основатели теории предельной полезности считали существование меры полезности само собой разумеющимся фактом. Менгер и Вальрас никогда всерьез не ставили вопроса об измеримости полезности. Джевонс вначале отрицал возможность измере­ния полезности, а затем предложил способ ее измерения на основе приблизительного постоянства предельной полезности денег — метода, который впоследствии принял и усовершенствовал Маршалл. Джевонс отрицал также возможность межличностных сопоставлений полезностей, отмечая, что теория цены не требует подобных сопостав­лений, но затем стал делать суждения относительно благосостояния, предполагающие и количественное измерение полезности, и межличностные сопоставления. С другой стороны, Менгер и Вальрас не видели трудностей в межличностном сопоставлении полезностей. Все три основателя теории предельной полезности имели дело с так называемой "аддитивной функцией полезности", рассматривая полезность товара как функцию количества этого товара, не зависящую от количеств других потребляемых товаров. Они уделяли очень мало внимания точной форме функции полезности и считали закон убывающей предельной полезности общепризнанным фактом. Вальрас в своей книге рисовал линейную функцию предельной полезности. Менгеровские таблицы также предполагали линейные функции. Большинство кривых Джевонса были выпуклы книзу.

Ни один из них не признавал никаких исключений из фундаментального закона убывающей предельной полезности, а Джевонс даже предложил свои доказательства того, что никаких исключений не существует.

Более того, только Вал ьрасу удалось увязать действительную полезность со спро­сом, хотя и он не смог достаточно строго показать, какое влияние убывающая предель­ная полезность оказывает на поведение потребителей, на их спрос: он начал свой анализ исходя из данных кривых спроса и вывел условия рыночного равновесия до того, как он сказал хотя бы слово относительно полезности. С другой стороны, Дже­вонс связал полезность и спрос с помощью неадекватной концепции "торгующих сторон" (trading bodies), а Менгер просто постулировал определенные цены спроса, которые каким-то образом отражали предельные полезности. Ни одна из этих техни­ческих проблем теории полезности не прояснилась вплоть до 90-х годов, а некоторые оставались неясными до самого конца прошлого столетия. Изложение теории полез­ности Маршаллом выше того, что сделали Джевонс и Вальрас, но последующие изда­ния маршалловских "Принципов" отличаются растущей осторожностью и сдержанно­стью, поскольку работы Эджуорта, Фишера и Парето начали подрывать прежние представления об измеримости, аддитивности и сопоставимости полезностей. Прежде чем рассмотреть, как Маршалл справился с некоторыми техническими трудностями теории полезности, следует дать обзор тех теоретических проблем, которые мешали теоретическому прогрессу в этой области.

Измеримость полезности

Предположим, что потребитель в соответствии со своими предпочтениями избирает товары А, В, С и D. При данном устойчивом ранжировании (предпочтений) этих четырех товаров мы можем сконструировать индекс полезности для данного потреби­теля, придав каждому из товаров какое-нибудь произвольное число, но сохранив порядок ранжирования: бесконечное количество подобных показателей будет ранжи­ровать эти четыре избранных товара одинаково (см. табл. 9-1 и 9-2). Если при всех возможных числах неизменным остается только порядок, то мы имеем ординальную (порядковую) полезность, функцию "постоянную с точностью до монотонного преоб­разования". Предположим, что мы сконструируем новую серию, показывающую тот же порядок предпочтений среди А, В, С и D. Но теперь мы введем несколько более сильные ограничения для этих индексов: их разница должна описываться с помощью прибавления константы и умножения на константу. То есть если х—это один индекс, а у — следующий, тогда у получен на основе уравнения у == aх + b, где а и b — константы. Следовательно, разница между двумя индексами, полученными таким образом, определяется точкой отсчета и произвольной единицей измерения. Подо-

бные кардинальные (количественные) показатели по понятной причине называют "постоянными с точностью до линейного преобразования".

Эти два типа шкал полезности решительно отличаются в одном отношении. Шка­лы, получаемые на базе монотонного преобразования друг друга, имеют одно и то же направление — это единственно общее для них свойство. Шкалы, получаемые на базе линейного преобразования показателей, предполагают нечто более строгое: если ин­тервалы между показателями одной шкалы последовательно увеличиваются или сокращаются, то интервалы других шкал также последовательно увеличиваются или уменьшаются в той же степени. Если мы выберем одну из бесконечного числа функ­ций полезности, удовлетворяющих требованию A > В > С > D с точностью до линей­ного преобразования, мы можем сравнивать различия между последовательными интервалами и делать, скажем, такой вывод: полезность A, U_Aпревышает полезность В, U_B в большей мере, чем U_A превышает U_C. В нашем примере мы можем сказать, что разница между полезностью A и полезностью В (U_A >U_B) в 2 раза выше, чем разница между полезностью В и С (U_B > U_C), — утверждение совершенно бессмысленное, если мы используем функцию полезности, постоянную с точностью до монотонного преоб­разования.

Измеримость с точностью до линейного преобразования требует знания знака не только первых разностей, но и вторых разностей значений функции полезности [т.е. разности разностей. — Прим. ред.]: первая разность говорит нам о направленности предпочтений; вторая разность — об интенсивности предпочтений. Если же мы в состоянии всего лишь ранжировать порядковые (ординальные) полезности с точно­стью до монотонных преобразований, то о предельной полезности можно сказать лишь то, что она положительна или отрицательна. Понятие же возрастающей или снижаю­щейся предельной полезности смысла не имеет. Но если полезность можно измерить количественна (кардиналъно) с точностью до линейного преобразования, то первая и

вторая производные функции полезности обретают смысл; величина первой произ­водной является показателем предельной полезности, а отрицательный знак второй производной означает действие закона уменьшающейся предельной полезности. По­лезность, измеряемая таким способом, аналогична температуре, измеряемой термо­метром, градуированным по шкале Цельсия или Фаренгейта, поскольку шкала Фа­ренгейта соотносится со шкалой Цельсия по формуле 9/5 С° + 32 = F⁰, можно делать выводы об изменениях температуры независимо от вида применяемого термометра.

2. Операциональное измерение полезности

Операциональное построение порядковой шкалы полезностей представляется делом простым: мы просто позволяем индивиду выбирать товары и затем записываем серию чисел, сохраняя тот порядок, в котором он эти товары выбирал (ранжировал). Но для того, чтобы построить количественную шкалу полезностей, нам следует попросить индивида осуществить так называемый "мысленный эксперимент", вообразив две ситуации: когда он выбрал товар А, а не В, мы должны вновь дать ему товар В и попросить его сделать выбор между В и С и сравнить интенсивность предпочтений в этих двух ситуациях. Это чисто субъективная процедура, но поскольку полезность одного товара абсолютно не зависит от полезности всех других товаров, она фактиче­ски дает возможность сконструировать количественную шкалу полезностей.

Впервые это было продемонстрировано Ирвингом Фишером в его очерке "Стати­стический метод измерения "предельной полезности" и проверка справедливости про­грессивного подоходного налога" ("A Statistical Method of Measuring "Marginal Utility" and Testing the Justice of a Progressive Income Tax", 1927). Метод Фишера состоит в следую­щем: дадим индивиду произвольное количество какого-либо товара, например 100 батонов хлеба. Пусть предельная полезность 100 батонов равна одному "ютилю" — единице измерения полезности. Теперь, начиная с позиции, когда у этого индивида отсутствует молоко, найдем минимальное количество молока, которое он приобретет в обмен на сотый батон хлеба, который стоит один "штиль". Зная величину первого прироста количества молока, скажем, 3 кубических сантиметра, повторим экспери­мент со вторым приращением и далее, показывая при этом, что типичный индивид, конечно, будет требовать все большее количество молока за отказ от каждого допол­нительного батона хлеба. Таким образом, мы получим ряд чисел, показывающих количества молока, необходимые для получения равного прироста полезности. На базе этого ряда мы получим соответствующий ряд показателей общей полезности потребленного молока (см. табл. 9-3). Суммируя приросты количеств молока (3,4,5, б, 7), мы можем получить также ряд чисел, показывающих совокупную полезность, доставляемую последовательными количествами выпитого молока (3, 7,12, 18, 25). Интерполируя, мы можем, таким образом, найти величину полезности, получаемую от равных приростов количества молока (табл. 9-4).

Предположив, что индивид способен делать последовательный выбор между дву­мя конкретными количествами двух товаров, мы сможем определить эту функцию полезности с точностью до линейного преобразования. Но если предельная полезность молока зависит не только от количества молока, но и от количества других потреблен­ных продуктов питания, то, как показал Фишер, мы получим новую функцию полез­ности, относящуюся к прежней нелинейным образом, если мы изменили товар, с помощью которого измерялась полезность молока. Если мы откажемся от концепции "аддитивной функции полезности" с одной переменной, а именно U_A = f(A), U_B= f(B) и т.д., и примем "обобщенную" функцию полезности, а именно U_a = f(A, В, С,...), U_B = f(B, А, С,...), то мы уже не сможем измерять полезность в абсолютных величинах методом попарного выбора.

Идея обобщенной функции полезности была введена Эджуортом в работе "Mathematical Psychics" (1881) и развита Фишером в его знаменитой докторской дис­сертации "Mathematical Investigations" (1892). И хотя большинство экономистов при­знали взаимозависимость полезностей разных благ и, следовательно, невозможность существования аддитивной функции полезности, отказ от нее происходил медленно и с большим сопротивлением. Гипотеза универсальной "независимости" товаров, как мы увидим, исходит из того, что ни один товар не является "худшим" (inferior), т.е. не является тем товаром, покупки которого уменьшаются по мере роста дохода. Эта предпосылка противоречит фактам, свидетельствующим, что многие товары, если их определить достаточно узко, начиная с некоторых уровней дохода, действительно становятся "худшими". Следовательно, гипотезу универсальной "независимости" сле­дует отвергнуть. Однако обобщенная функция полезности делает простую операци­онную процедуру по определению кардинальной полезности невозможной. Даже если мы примем возможность измерения полезности как данное, мы не сможем строго вывести из закона убывающей предельной полезности возрастающих функций спроса от дохода и убывающих кривых спроса от цены; результатом является более сложная и неоднозначная теория спроса. Поэтому нетрудно понять, почему в этот период большинство авторов, в особенности не искушенных в математике, предпочитали работать с аддитивными функциями полезности.

Вот все, что можно сказать об измерении полезности с точки зрения теории спроса. А как обстоят дела с измерением полезности с точки зрения теории благосостояния? Здесь даже измерения с точностью до линейного преобразования могут оказаться недостаточными. Даже если предположить, что мы можем произвести подобные из­мерения, пользуясь аддитивными функциями полезности, отсюда вовсе не следует, что мы можем интегрировать кривые предельных полезностей и таким образом полу­чить соответствующие совокупные полезности. Суммы, полученные путем сложения интервалов и рассчитанные на базе двух показателей, идентичных с точностью до линейного преобразования, будут не равны, поскольку и нулевая точка отсчета, и единица измерения избраны произвольно. Мы можем сказать, что температура с воскресенья до понедельника выросла в 2 раза больше, чем с понедельника до вторни­ка, и это будет верно независимо от того, пользуемся мы градусами Фаренгейта или Цельсия. Но мы не можем сказать, что температура в понедельник была в 2 раза выше, чем в воскресенье, поскольку это утверждение зависит уже от того, каким термомет­ром мы пользуемся: например 20°С = 68°F, a 40°C = 104°F. Суммы измерений темпе­ратуры не имеют смысла, поскольку результаты отличаются в зависимости от избран­ного масштаба измерения. Что касается полезности, то возможность ее измерения с точностью до линейного преобразования дает нам знак предельной полезности, а также степень ее изменения, но не позволяет установить общую полезность набора товаров на основе суммирования их предельных полезностей.

Чтобы получить абсолютную величину совокупной полезности набора товаров для отдельного индивида, мы должны были бы иметь возможность рассчитать соотно­шения не только между разностями значений функции полезности, но и между самими этими значениями. А это предполагает измерение "с точностью до пропорци­онального преобразования", возможное лишь в том случае, если все показатели крат-

вы одной константе и различаются только количеством умножений на нее. Если бы полезность можно было измерить таким способом, то этот процесс был бы похож скорее на измерение веса и длины, когда нулевая точка отсчета точно определена, чем на измерение температуры, при котором нулевая точка зависит от принятого масш­таба измерения. Говоря несколько иначе, в ординалистской теории полезности нам известна только серия контурных линий на карте горы индивидуальной полезности, но мы не в состоянии судить о том, является эта гора Эверестом или кротовым холмиком. В кардиналистской теории мы можем по крайней мере сравнивать рассто­яния между контурными линиями и иметь представление об очертаниях горы. Однако мы по-прежнему не знаем ее высоты, поскольку нам неизвестно, где она начинается и насколько круто поднимаются ее склоны, единица и начало измерения здесь совер­шенно произвольны. Однако, как доказывал Маршалл, при некоторых жестких усло­виях мы можем определить абсолютную высоту горы. Предполагая постоянную пре­дельную полезность денег, теория благосостояния Маршалла достигла наивысшей возможности в измерении полезности, а именно измерения с точностью до общего множителя.

3. Гипотеза Бернулли

До этого момента мы рассматривали теорию полезности как средство прогнозирова­ния потребительского выбора, осуществляемого среди некоторого количества "извест­ных перспектив", или по крайней мере прогнозирования того, как потребители оцени­вают наборы "известных перспектив". Но как объяснить поведение потребителей в условиях неопределенности? Люди покупают страховой полис, тем самым предпочи­тая определенность неопределенности; но они также любят азартные игры, предпочи­тая неопределенность определенности. Возможно ли рационализировать этот род поведения, предполагая, что люди поступают так с целью максимизации "математи­ческого ожидания" своего дохода?

Все попытки определить функцию полезности на основе наблюдения за реакцией индивидов на вероятностные ситуации восходят к статье Бернулли о Санкт-Петер­бургском парадоксе (1738 г.). Суть парадокса в следующем: монета бросается до тех пор, пока она не ляжет лицевой стороной вверх; если это произойдет при первом броске, А платит В 1 долл.; при втором — 2 долл.; при третьем — 4 долл. и т.д., т. е. А всякий раз уплачивает 2^n-1 долл. за n-ый бросок, при котором монета ложится лицевой стороной вверх. Какую плату захочет уплатить В за право играть в такую игру, если это "честная игра"? "Честной игрой" считается такая игра, в которой от игрока на каждой стадии игры никогда не требуют заплатить больше, чем общее математиче­ское ожидание успеха, т.е. страховую стоимость (actuarial value of gamble). Ожидаемый выигрыш или ожидаемая потеря дохода от "честного пари", следовательно, всегда равны нулю. Математическое ожидание успеха при первом бросании монеты равно р * 1 долл. = 1/2 • 1 долл. = 0,50 долл.; при втором бросании оно равно 1/2*1/2 • 2 долл. = 0,50 долл.; при n-м бросании оно составит (1/2)ⁿ • 2^n-1 долл. = (2)^n-1 • 2^n-1 долл. =2^-1 долл. = 0,50 долл. Поскольку общее ожидание Е представляет собой сумму ожи­даний на каждой стадии игры, то E = 0,50 долл. + 0,50 долл. +... Сумма этого беско­нечного ряда бесконечно велика, так что В должен заплатить А бесконечную сумму денег за право играть в подобную "честную игру". Поскольку люди явно не захотят платить бесконечно большие ставки за "честную игру", то предпосылка, согласно которой индивиды действуют якобы в интересах максимизации математического ожидания своего дохода, оказывается противоречивой.

Одним из решений этого парадокса может быть определение верхней границы выигрыша. Однако Бернулли предложил другое решение. Он утверждал, что люди руководствуются не "математическим ожиданием", а "моральным ожиданием" успеха, при котором вероятность взвешивается по полезности дохода. К тому же предельная полезность дохода с каждым приростом последнего снижается. При снижающейся предельной полезности денежного дохода люди будут настаивать на увеличивающих-

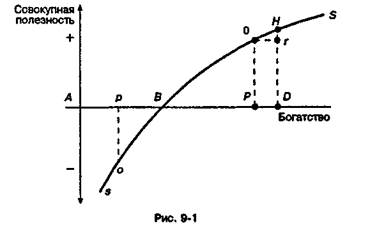
ся выплатах, с тем чтобы компенсировать риск данной потери: никто не станет платить 1 долл. за шанс выиграть 2 долл. с вероятностью 50%. Бернулли иллюстрировал свое доказательство графически (см. рис. 9-1).

Богатство индивида в самом начале составляет АB, а шанс выиграть ВР равен 50%. Общая полезность выигрыша и потеря полезности, связанная с платой за право уча­ствовать в игре, измеряются вдоль оси ординат. Если бы sBS была прямой линией, индивид платил бы сумму рВ, в точности равную ожидаемому выигрышу ВР. Посколь­ку кривая полезности дохода вогнута книзу, рВ представляет собой самую большую сумму, которую придется уплатить за 50%-й шанс выиграть ВР, причем в этой точке полезность выигрыша РО равна потере полезности от платы за игруро. Далее Бернул­ли предположил, что кривая является логарифмической. Если rН представляет собой полезность бесконечно малой величины выигрыша PD для индивида, имеющего сум­му денег АР, то, как полагает Бернулли, rН прямо пропорционально PD и обратно пропорционально АР. То есть допустим, что Р — это величина "имущества" индивида; a dP — приращение этого имущества; тогда

dU=k dP/P или dU/dP=k/P,где k - постоянная величина.

Предположим вместе с Бернулли, что с — величина "имущества", необходимая для существования, тогда общая полезность, получаемая от дохода Р, может быть пред­ставлена определенным интегралом:

∫^p_c k dP/P = k(logP-logc) = k log P/c,

где с — постоянная интегрирования.

"Гипотеза Бернулли" утверждает, что dU, т.е. предельная полезность дохода, сни­жается тем же темпом (в %), каким увеличивается доход независимо от величины k. График предельной полезности дохода принимает, таким образом, форму равнобоч­ной гиперболы, а это означает, что увеличение дохода на 10% ведет к снижению на 10% его предельной полезности независимо от его уровня. Но, как мы увидим далее, это всего лишь один представитель семейства возможных графиков предельной по­лезности дохода.

4. Азартные игры и страхование

В 60-х годах XIX столетия гипотеза Бернулли получила дальнейшее развитие в работах вновь возникшего направления психофизики. Так называемый закон Вебе-ра—Фехнера гласил, что осязаемые различия в ощущениях прямо пропорциональны интенсивности стимулов: ощущения представляют собой логарифмическую функ­цию стимулов. Психофизические эксперименты Фехнера, видимо, подтверждали ги­потезу Бернулли, во всяком случае если "стимулы" отождествить с приростом дохода,

а "ощущения" — с полезностью. Однако ни Менгер, ни Вальрас не обратили внимания на закон Вебера—Фехнера. Но Джевонс был знаком с работой Фехнера, признал он и вывод из гипотезы Бернулли, согласно которому "игра в долгосрочном аспекте пред­ставляет собой надежный способ потери полезности". Маршалл в этом отношении был его последователем и соглашался с тем, что принцип максимизации полезности не может быть применен для объяснения выбора в условиях неопределенности. Если полезность данной выигранной суммы всегда меньше полезности потерянной, то рациональный индивид выберет страховку с равными или слегка предпочтительными шансами, но никогда не станет играть просто в "честную игру": он лучше заплатит больше 1 долл., с тем чтобы защитить себя от 1%-й вероятности потерять 100 долл., чем заплатит 1 долл. за 1%-ю вероятность выиграть 100 долл. Широко распространен­ный феномен покупки лотерейных билетов на "неравных" условиях следует объяснять "пристрастием к азартным играм". Другими словами, поступки людей вряд ли объяс­нимы их стремлением к максимизации ожидаемой полезности дохода.

Запрет Маршалла на использование теории полезности при анализе выбора в условиях неопределенности длился вплоть до недавнего времени, когда Нейман и Моргенштерн показали, что это как раз тот случай, когда можно использовать проце­дуру для измерения полезности с точностью до линейного преобразования*. Правда, это мало что дает для теории потребления, которая предполагает, что индивид обычно выбирает среди известных альтернатив. Но это означает, что в одно прекрасное время мы сможем измерять кривую полезности дохода в абсолютных величинах. Эмпири­ческие исследования в духе идей Неймана—Моргенштерна уже дали многообещаю­щие результаты, поэтому ученые вернулись к проблеме рационализации на первый взгляд противоречивого поведения индивидов, которые страхуются от крупных по­терь и в то же время играют на "равных" условиях (at "fail" odds).

Одна из таких гипотез, гипотеза Фридмена—Сэведжа, гласит, что кривая полез­ности дохода вогнута книзу в нижней и верхней своей части, но выпукла книзу — а это означает растущую предельную полезность дохода — в середине. И гипотеза Бернулли, и гипотеза Фридмена—Сэведжа предполагают, что полезность зависит от абсолютного уровня дохода: при данной кривой полезности дохода индивиды выбира­ют между альтернативными ситуациями, двигаясь вдоль нее. Однако полезность дохода можно соотнести с изменениями в уровне дохода, и в этом случае мы получаем более простое объяснение того факта, что большинство индивидов играют в азартные игры и в то же время принимают меры по страхованию от риска. Гипотеза Марковица объясняет этот феномен тем, что кривая полезности дохода содержит три, а не две точки перегиба, при этом нынешний уровень дохода независимо от его абсолютного размера находится в средней точке перегиба (см. рис. 9-3). Небольшие приращения дохода дают растущую предельную полезность, в то время как большие выигрыши порождают убывающую предельную полезность; это отражает отрицательное отно­шение людей к игре по-крупному и их готовность делать мелкие "честные ставки". В то же время небольшие сокращения дохода порождают растущее ощущение наноси­мого ущерба, а отсюда — стремление оградить себя от мелких потерь при полном безразличии к действительно большим утратам.

* Сущность процедуры, предложенной Нейманом и Моргенштерном, состоит в следующем: преположим, индивид находит, что u_A > U_b > U_c; возьмем лотерейный билет с выигрышем в виде А или С и предложим нашему герою выбор между возможностью получить В или взять лотерейный билет, на который с вероятностью р выпадет А или с вероятностью (1 - p) выпадет С; находим, что р обеспечивает следующее равенство: pU_A + (1 — р) U_c = U_b. К примеру, у индивида имеется вероятность 1/5 не выиграть ничего и вероятность 4/5 выиграть 10 долл. "Математическое ожидание" от приобретения лотерейного билета составит в этом случае (1/5 • 0 долл.) + (4/5 • 10 долл.) = 8 долл.; но "моральное ожидание" равно (1/5 • 0 долл.) + (4/5 • 1 долл.) — 4/5, где U полезность выигрыша 10 долл. установлена произвольно и равна единице. Предположим, мы обнаруживаем, что при условии, когда В = 6 долл., u_b = 4/5 u_a, индивиду все равно — получать б долл. или лотерейный билет. Изменяя величину вероятностей в этой игре и определяя среднюю полезность выигрышей, равную различным Bs, мы сможем вычертить всю кривую полезности, причем единица измерения и нулевая точка определяются произвольно. См. рис. 9-2.

Суть этих последних исследований состоит в том, чтобы показать, что убывающая предельная полезность денежного дохода — это совсем не то, что убывающая предель­ная полезность какого-либо конкретного товара. Бели даже все вещи, которые можно купить на деньги, подчиняются закону убывающей предельной полезности, отсюда вовсе не следует, что тому же закону подчиняется и денежный доход. Можно рацио­нализировать поведение людей с помощью конкретной кривой полезности дохода, и, возможно, в один прекрасный день мы будем способны измерять количественную полезность дохода. Когда индивид готов уплатить 10 долл. за шанс выиграть 20 долл. при вероятности 50 на 50, то мы можем сделать вывод, что при его уровне дохода предельная полезность денег для него является постоянной. Если же он настаивает на "более чем равных шансах", то мы можем заключить, что он оценивает потерю 10 долл. выше, чем выигрыш от 10 долл., из чего следует, что предельная полезность денег, с его точки зрения, снижается и, наоборот, растет, если он готов играть на невыгодных условиях (меньших, чем при "честной игре"). Однако теория спроса вовсе не требует количественного измерения полезности; и никто еще не сумел изобрести такую про­цедуру, которая позволяла бы измерить выбор индивидов среди известных альтерна­тив с точностью до линейного преобразования. Маршалл эту проблему аккуратно обходит, сводя свой анализ к товарам, расходы на которые составляют небольшую часть общих расходов потребителя. Для таких товаров предельную полезность денеж­ного дохода можно считать приблизительно постоянной, расчищая тем самым путь для простого перехода от полезности к спросу.

5. Гипотеза Бернулли и прогрессивное налогообложение

Перед тем как перейти к теории спроса, рассмотрим вкратце один из популярных способов использования гипотезы Бернулли в тот период, а именно в целях оправда-

ния прогрессивного налогообложения. С первого взгляда может показаться, что кон­цепция снижающейся предельной полезности дохода всегда оправдывает прогрессив­ное налогообложение. Но это не так. Предположим, что все индивиды с одинаковым доходом имеют одинаковую способность удовлетворять свои потребности, так что один и тот же график полезности дохода применим ко всем налогоплательщикам; предположим далее, что мы хотим распределить налоговые платежи таким образом, чтобы все несли "равные жертвы", измеренные величиной уплачиваемого дохода; и тем не менее окажется, что мы придем к разным выводам в зависимости от того, что мы хотим уравнивать — абсолютную, пропорциональную или предельную величину жертвы. При условии равенства абсолютной величины жертвы налоги распределя­ются таким образом, чтобы изъять одинаковую абсолютную величину общей полез­ности дохода у каждого индивида. При пропорциональном равенстве жертвы мы попытаемся извлечь одинаковую долю общей полезности дохода каждого индивида; при этой схеме "богатые" заплатят больше, а бедные — меньше, чем в предыдущем случае. При равенстве предельной жертвы мы минимизируем общую величину жер­твы, при этом каждый индивид теряет одинаковую величину предельной полезности. A priori неясно, какую из этих концепций следует применить; Сиджвик и Маршалл склонялись в пользу первой; Коэн—Стюарт, известный голландский специалист по государственным финансам, предпочитал вторую; Эджуорт и Питу выступали за третью. Но какая бы концепция ни была избрана, фактическая структура налоговых ставок, необходимая для того, чтобы выполнить требование "равных жертв", зависит от конкретной формы кривой полезности дохода.

Если известно лишь то, что предельная полезность дохода снижается каким-то неопределенным темпом при всех его уровнях, тогда прогрессию в налогообложении, очевидно, можно оправдать на основе концепции равной предельной жертвы. Каким бы ни был отрицательный наклон кривой, эта концепция приближает наивысший доход к следующему за ним и т.д. до тех пор, пока не будет получена необходимая сумма налога. Чтобы обосновать прогрессию на основе концепций равной абсолют­ной или равной пропорциональной жертвы, требуется, чтобы кривая предельной полезности дохода была бы более крутой, чем кривая Бернулли, т.е. круче, чем равнобочная гипербола. Гипотеза Бернулли предполагает, что данное процентное увеличение дохода порождает точно такое же увеличение общей полезности незави­симо от уровня дохода. Отсюда следует, что в этом случае принцип равной абсолют­ной жертвы требует пропорционального налогообложения: индивид, доход которого в два раза превышает доход другого, должен платить и в два раза больше налогов в долларах. Но даже при условии равной пропорциональной жертвы само по себе снижение предельной полезности дохода, как показали Коэн—Стюарт и Эджуорт, не обязательно ведет к прогрессии налогообложения.

Кроме того, хотя предельная полезность дохода может снижаться при данном уровне дохода, его увеличение может вызвать сдвиг всей кривой вверх вследствие роста ожиданий. Если долгосрочный график, связывающий соответствующие точки сдвигающихся вверх краткосрочных кривых, носит постоянный характер, то в этом случае ни одна из трех концепций не может служить обоснованием прогрессивного налогообложения, а осуществление принципа равной абсолютной жертвы вообще потребует регрессивного налогообложения.

Дальнейшие осложнения возникают в том случае, если графики индивидуальной полезности взаимозависимы, так что удовлетворение, получаемое от дохода, зависит не только собственно от дохода индивида, но и от его места в шкале распределения доходов. И наконец, различия вкусов и, следовательно, различия кривых полезности дохода исключают всякую возможность вывести структуру (налоговых) ставок из любой концепции равной жертвы без предварительного межличностного сопоставле­ния полезности. Как только мы признаем, что люди различаются по способности удовлетворять свои желания, мы должны будем сделать вывод, что оптимальное распределение похода будет означать более высокие доходы для людей, более эффег

тивно извлекающих полезность, тоща остается лишь одна проблема — как найти этих индивидов.

Утверждалось, что в отсутствие специальных знаний мы должны исходить их того, что "все люди равны". Но это ошибка, которая часто возникает в случае, когда у нас есть две равновероятные альтернативы.

В отсутствие точных знаний предполагать, что кривые полезности дохода для отдельных лиц одинаковы, не более обоснованно, чем предполагать, что они различны. Вероятность обоих событий составляет 50% — и как только мы признаем, что они могут быть разными, мы сможем обосновать почти любое распределение дохода, введя в рассмотрение способность наслаждаться самим фактом получения дохода. К приме­ру, приведем не совсем приличное рассуждение Эджуорта в его работе 'Mathematical Psychics": "Если предположить, что способность получать удовольствие есть порожде­ние искусства и таланта... то тогда мы получим более глубокое, нежели то, что дает экономическая теория, объяснение более высокой оплаты за более приятный труд, которую получают представители аристократии искусств и таланта. Высшее удоволь­ствие от секса точно так же основано на более высокой способности мужчин испыты­вать счастье... Во всяком случае... имеет место удивительное сходство между выво­дами, вытекающими из принципа полезности, и современными дискуссиями о приви­легиях и обделенности в правах женского пола".

Возможно, единственный способ спасти предпосылку о том, что все мужчины и женщины имеют одинаковую способность получать удовлетворение от дохода, — это признать принцип: один человек — один голос, на котором базируются все наши политические институты. Налогообложение — это вопрос политического консенсуса, и это дает нам законное право укрыться за истинами, которые считаются самоочевид­ными. В результате проблема межличностных сравнений снимается, но по-прежнему с нами остается проблема, какую из концепций равной жертвы нам использовать.

Эта проблема в неоклассический период так и не была решена, а в некотором смысле она не решена и сегодня, хотя со временем идея равной предельной жертвы приобретала все больше и больше сторонников просто потому, что она обосновывала прогрессивный подоходный налог без предварительной спецификации конкретной формы кривой полезности дохода. Для англосаксонской традиции в области государ­ственных финансов вообще характерно, что вся проблема рассматривалась исключи­тельно с точки зрения налогов при полном игнорировании аспекта расходов. Очевид­но, что даже если предположить, что предельная полезность дохода с его ростом монотонно снижается, тем не менее найдутся люди, которые станут ратовать за пропорциональный или даже регрессивный подоходный налог, поскольку известно, что государственные расходы полностью используются на социальные цели, от кото­рых выигрывают только бедняки. В последние годы, в основном под влиянием италь­янских авторов, тенденция рассматривать налоговую прогрессию исключительно с точки зрения государственных доходов более или менее исчезла, и в результате резко упал интерес к закону убывающей предельной полезности дохода.

6. Выведение кривых спроса

Вернемся теперь к теории спроса. Маршалл был по сути первым автором, который вслед за Вальрасом ясно и определенно выводил кривую спроса из функции полезно­сти. В Математическом приложении II к своим "Принципам" Маршалл характеризует условия равновесия при потреблении товарах как MU_t = P<MU_n. В применении ко всем товарам это дает знакомый закон равенства отношений предельных полезностей к ценам:

MU_x/p_x=MU_y/p_y=MU_z/p_z=MU_n.

MU_n — это то, что Маршалл называет предельной полезностью денег. "Предельная полезность денег" — несколько неточный термин, поскольку на самом деле Маршалл имел в виду не предельную полезность запаса денег, принадлежащих индивиду, а предельную полезность потока его денежных доходов в единицу времени, скажем за

день или неделю. В условиях равновесия индивид захочет иметь запас денег, который дает ему возможность распоряжаться определенной долей k его реального дохода, так что:

M/P=k Y/P,

где Р — общий индекс цен. Так что формально нам следовало бы записать отдельную часть формулы распределения потребительского дохода, представляющую предель­ную полезность доллара, хранимого в виде неиспользуемого денежного остатка при данном уровне рыночных цен. Если индивид сберегает часть дохода, то нам надо учесть и нынешнюю предельную полезность будущих доходов от ценных бумаг, сверх их текущей цены. Однако в целях удобства мы будем исходить из предпосылки, что весь доход расходуется на текущее потребление. Приток денежных доходов, увеличи­вающий вначале запас денежных ср