ЗАНЯТИЕ 4
Тема: ОПЕРАЦИИ НАД ТЕНЗОРАМИ п.1. Связь между компонентами тензора с различными строениями индексов.
Задача 1. Показать, что если
Решение. Покажем, что с лева и с права стоят компоненты одного и того же тензора. Образуем линейные комбинации: 1) Поэтому, если 2) Требуемое показано. Задача 1 – пример «жонглирования» индексами. Задача 2. Матрица компонент
Решение. Осуществив «жонглирования» индексами, имеем
Порядок индексов матрицы (
Матрица определяет компоненты тензора в базисе Задача 3. Представить все формы записи тензоров 3-го ранга, используя тензорные произведения 3-х базисных векторов. Решение.
=
п.2. Тензорное (внешнее) произведение тензоров есть тензор, ранг которого равен сумме рангов сомножителей, а компоненты произведению компонент сомножителей. В частном случае диада - тензорное произведение двух векторов. Пусть Задача 4. Представить различные формы записи тензорного произведения вектора
Решение.
= п.3. Сложение тензоров определяется только для тензоров одной валентности; компоненты суммы определяются как сумма компонент слагаемых с одинаковым строением индексов. Задача 5. Показать, что если Решение. Используя правила преобразования компонент тензора. Получим
-это противоречит правилу преобразования компонент тензора. п.4. Скалярное произведение тензоров вычисляется следующим образом:
=
Скалярное произведение тензоров – тензор, ранг которого меньше суммы рангов сомножителей на два.
Задача 6. Доказать, что
Решение.
п.5. Двойное скалярное произведение вычисляется следующим образом:
Следом тензора называют двойное скалярное произведение тензора и метрического тензора. Обозначение следа:
Sp
Дополнительные задачи: 1. Найти выражение следа тензора второго ранга через его компоненты. 2. Записать различные формы представления скалярного произведения 2-х тензоров 2-го ранга. 3. Доказать, что 4. По определению степени тензора 5. Вычислить 6. Доказать, что 7. Вычислить Sp Решение.
1. Sp 2. Аналогично п.3. 3. Аналогично Задаче 6, доказываем 4. Так как 5. Аналогично
6. Воспользуемся определением следа тензора Sp 7. Так как
План занятия. 8 минут – проверка домашнего задания
Решение задач у доски: Пояснение п.1 (2 минут) Пояснение п.2 (2 минут) задача 1 (10 минут) задача 3 (5 минут)
Пояснение п.2 (2 минут) задача 4 (5 минут)
Пояснение п.3 (1 минут) задача 5 (5 минут)
Пояснение п.4 (2 минут) задача 6 (5 минут)
Пояснение п.5 (3 минут) Решение дополнительных задач: задача 1 (10 минут) задача 2 (10 минут) задача 4 (10 минут)
Домашнее задание: задача 2 Дополнительные задачи 3,5,6,7. Занятие 5 Тема: СВЕРТКА. АЛЬТЕРНИРОВАНИЕ И СИММЕТРИРОВАНИЕ,ТЕНЗОРНАЯ ПОВЕРХНОСТЬ. ГЛАВНЫЕ ЗНАЧЕНИЯ И ГЛАВНЫЕ НАПРАВЛЕНИЯ СИММЕТ-РИЧНОГО ТЕНЗОРА 2-го РАНГА п. 1. Обсуждение дополнительных задач Занятия 4 Решение.
Осуществляя "жонглирование" индексами, получим:
3. Метрический тензор выполняет роль своеобразной"единицы":
(см.также задачу 6 занятия 4). 4. Вычисление компонент квадрата и куба тензора 2-го ранга требуется для нахождения его инвариантов. Имеем:
Степени тензора 2-го ранга-тензора того же ранга. 5. Если (инвариант). Действительно,
б. Аналогично 5 имеем
1. Учитывая предыдущие упражнения, сразу записываем
п.2. Свертка - операция, выполняемая над тензором, компоненты которого имеют по крайней мере один но- и один контравариантный индекс. Свертка тензора
к тензору тензорного произведения. Например, Задача 1. Показать, что свертка тензора по индексам п.3. Альтерн ирование и симметрирование тензора- выделение его антисимметричной и симметричной частей. Тензор называется симметричным (антисимметричным) по индексам Тождество;
лежит в основе указанных операций для тензоров 2-го ранга. Задача 2. Матрица компонент
Определить матрицы компонент симметричной и антисимметричной частей тензора. Решение. Используя тождество, получим:
вправой части равенства находятся искомые матрицы. Задача 3. Доказать, что свертка симметричного тензора и антисимметричного равна нулю. Рассмотреть случай тензоров 2-го ранга. Решение. Пусть
(по п. 4. Тензорная поверхность симметричного тензора 2 - горанга в данной точке определяется уравнением:
Квадратичная форма ку симметричных тензоров - компонента бесконечного малого вектора Конец этого вектора лежит на тензорной поверхности - поверхности 2-гo порядка. В осях, соответствующих главным направлениям, уравнение поверхности приводится к каноническому виду. Единичный вектор
Задача 4. Показать, что контравариантные компоненты вектора удовлетворяют системе уравнений:
Решение. Имеем
отсюда следует искомая система однородных линейных алгебраических уравнений. Условие нетривиальности решения этой системы определяет характеристическое уравнение
Решением последнего уравнения являются главные значения тензора
нетривиальное решение системы Задача 5. Найти главные значения и главные направления тензора имеет виц:
Решение. Характеристическое уравнение имеет в данном случае виц:
Корни этого уравнения определяют три главных значения
щие
Первые два уравнения имеют лишь тривиальное ранение, так как детерминант этой однородной системы отличен от нуля (равен 3):
Компоненты ляются из системы:
Получаем соответствующие
Получаем Если ме координат, а вектор
Вектора главных направлений имеют следующее разложение по направлениям ортов
Дополнительные задачи. 1. Установить, го каким индексам симметричны или антисим -метричны тензоры, компоненты которых удовлетворяют условиям
2. Доказать, что если тензор с компонентами метричен по индексам то он равен нулю. 3.Зная матрицу
где представления;
Зная матрицу этих представлений. 5. Показать, что след антисимметричной части тензора 2-го ранга равен нулю. 6. Найти главные значения и главные направления
З а н я т и е 6 Тема. ДИФФЕРЕНЦИРОВАНИЕ ВЕКТОРА И ТЕНЗОРА ПО КООРДИНАТЕ В общем случае при переходе от точки к точке изменяются и компоненты вектора (тензора), и величины, и направления базисных векторов. Задача 1. Исходя из введения коэффициентов связности цирования вектора
Решение. Дифференцируем инвариантные представления вектора
переобозначая во втором слагаемом немые индексы (вместо Задача 2. Доказать формулу представления ковариантной производной от ковариантной компоненты вектора
Решение. Пусть Разложим Коэффициенты Продифференцируем скалярное произведение
В итоге
где
Задача 3. Показать, что риантная компонента вектора есть компонента тензора. Решение. Образуем свертку по
т.е. представление остается инвариантным и одновременно раскладываемым в базисе Задача 4. Исходя из определения коэффициентов связности (см.задачу 1), вывести формулу дифференцирования компоненты тензора 2-го ранга, контравариантной по индексам, по координате Решение.
Коэффициенты связности выражаются черев компоненты метрического тензора и их производные:
Задача 5. Доказать эту формулу. Решение. Запишем выражение производных от скалярных функций.
В эвклидовом пространстве можно ввести вектор
Вримановом пространстве производных, получим:
Далее, доумножая левую и правую части на ку по формулу. Задача б. Зная компоненты матриц найти выражения коэффициентов стемы координат. Решение. В данном случае
Обе матрицы с нулевыми недиагональными членами, с компонентами, не зависящими от
Присваиваем
Дополнительные задачи. 1. Найти выражение ковариантной производной от компоненты тензора 2-го ранга со смешанным строением индексов. 2. Доказать формулу: 3. Доказать формулу:
4. Найти 5. Вычислить ковариантные производные от компонент вектора в сферической системе координат: 3 а н я т и е 7. Тема: ОСНОВНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ ОПЕРАТОРЫ (ГРАДИЕНТ, ДИВЕРГЕНЦИЯ). ФИЗИЧЕСКИЕ КОМПОНЕНТЫ ВЕКТОРА Представление дифференциальных операторов осуществляется с помощью символического оператора Гамильтона
Последнее выражение - полиадное произведение. Задача 1. Пусть координат. Показать, что компоненты. Решение.
системе координат Ответ.
Задача 3. Тот же вопрос в случае сферической системы координат Решение. Так как производная от
ковариантные компоненты имеют вид:
п.2. Оператор "дивергенция" координатах. Решение. Вуказанных координатах коэффициенты связности равны нулю, поэтому
Задача 5. Выразить произвольной системы координат. Решение.
Сумма коэффициентов Вейла: где Задача 6. Проверить формулу Вейла в случае ортогональной системы координат. Решение. В указанном случае имеем:
но в случае ортогональной системы(суммирования по Поэтому
Но Требуемое показано. Задача 7. Доказать формулу; компоненты вектора. Решение. "Немые" "индексы можно обозначить любыми буквами, переобозначим все черев Задача 8.
|

 компоненты метрического тензора, то компоненты тензора
компоненты метрического тензора, то компоненты тензора 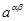 преобразуются в компоненты со смешанным строением индексов по формуле:
преобразуются в компоненты со смешанным строением индексов по формуле:


 =
= 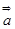
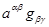
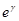 =
= 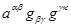
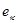 =
= 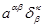

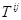 тензора 2-го ранга имеет вид:
тензора 2-го ранга имеет вид: , метрическая матрица (
, метрическая матрица ( ) равна
) равна . Определить матрицу компонент
. Определить матрицу компонент 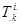 .
.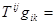

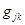 ) несущественен. В результате произведения матриц находим искомую:
) несущественен. В результате произведения матриц находим искомую: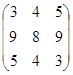 =(
=(

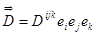 =
= 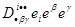 =
= 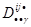

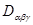



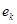 =
= 

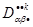
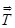 =
= 

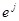 ,
, 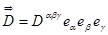 . Тензорное произведение
. Тензорное произведение  =
= 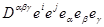 - тензор 5-го ранга.
- тензор 5-го ранга.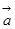 и тензора второго ранга
и тензора второго ранга 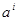

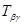

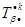
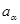

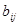 компоненты тензора, то комплекс
компоненты тензора, то комплекс 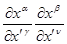
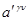 +
+ 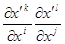
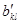
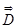 =
= 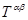

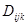


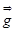 ×
× 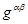

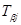



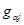 =
= 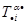

 =
=  =
= 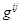
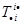 .
.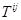
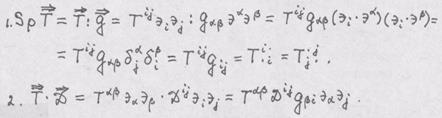
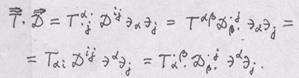
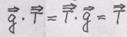 Действительно,
Действительно, 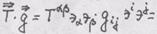


 - тензор 2-го ранга, то
- тензор 2-го ранга, то  - скаляр
- скаляр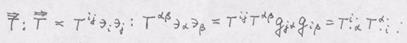

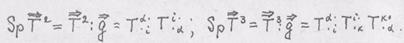
 по
по  и
и это переход к тензору
это переход к тензору  , по
, по  и
и  - переход
- переход . Свертка двух тензоров есть свертка их
. Свертка двух тензоров есть свертка их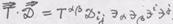 Свертка по индексам
Свертка по индексам  и
и  дает тензор
дает тензор 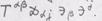

 и
и 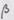 равна
равна 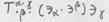 _Решение. По определению свертка данного тензора есть вектор
_Решение. По определению свертка данного тензора есть вектор  . С другой стороны,
. С другой стороны, 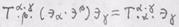
 и
и  , если компоненты его не меняются (изменяют только знак) при перестановке
, если компоненты его не меняются (изменяют только знак) при перестановке  и
и  ; для тензоров 2-го- ранга не имеет смысла указывать, по каким индексам симметрия или антисимметрия.
; для тензоров 2-го- ранга не имеет смысла указывать, по каким индексам симметрия или антисимметрия.
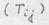 тензора имеет вид:
тензора имеет вид:

 -симметричный,
-симметричный,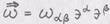 антисимметричный тензоры.
антисимметричный тензоры.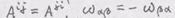 Свертка тензорного произведения
Свертка тензорного произведения 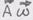 по обоим индексам равна
по обоим индексам равна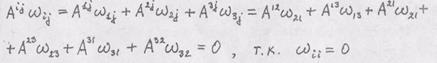
 нет суммирования).
нет суммирования).
 представляет собой сверт-
представляет собой сверт- и
и  . Здесь
. Здесь 
 в данной точке.
в данной точке.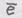 , определяющий главное направление, удовлетворяет соотношению:
, определяющий главное направление, удовлетворяет соотношению:
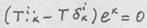
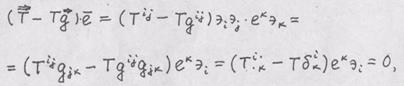
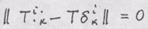
 . Каждому значению
. Каждому значению  соответствует свое
соответствует свое Компоненты
Компоненты  определяют три главных направления тензора.
определяют три главных направления тензора. в точке, матрица компонент которого
в точке, матрица компонент которого 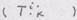


 ,
,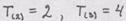 Компоненты
Компоненты 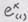 , соответствую-
, соответствую- , определяются из системы;
, определяются из системы;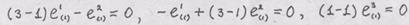
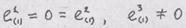
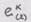 , соответствующие
, соответствующие 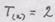 , опреде-
, опреде-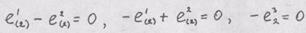
 ,
,  . Компоненты
. Компоненты 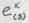
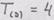 , определяются из системы;
, определяются из системы;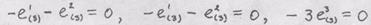
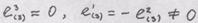
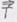 определен компонентами
определен компонентами 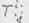 в декартовой систе-
в декартовой систе-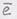 единичный, то
единичный, то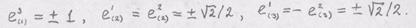
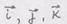 :
: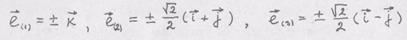
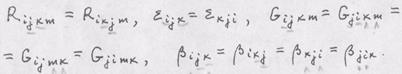
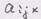 сим-
сим- и
и 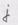 , антисимметричен по
, антисимметричен по 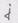 и
и 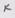 ,
,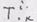 (см.задачу 5), вычислить
(см.задачу 5), вычислить (ответ 3; 21; 73). 4. Характеристическое уравнение можно представить в форме:
(ответ 3; 21; 73). 4. Характеристическое уравнение можно представить в форме: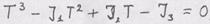
 - скалярные инварианты тензора 2-го ранга, имеющие
- скалярные инварианты тензора 2-го ранга, имеющие
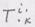 (см.задачу 5), проверить справедливость
(см.задачу 5), проверить справедливость
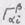 в равенстве
в равенстве 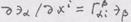 , доказать формулу дифферен-
, доказать формулу дифферен- по координате:
по координате: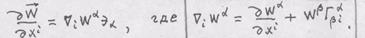
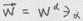 . Имеем:
. Имеем:
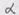 берем
берем 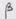 , вместо
, вместо  берем
берем  ), получаем искомое.
), получаем искомое.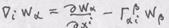
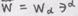 . Тогда
. Тогда 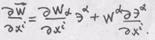
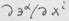 в том же ба8исе, что и
в том же ба8исе, что и 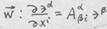
 выражаются черев коэффициенты связности.
выражаются черев коэффициенты связности.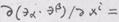
 . Сдругой стороны,
. Сдругой стороны,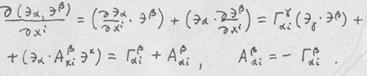

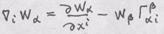
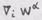 , где
, где 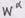 - контрава-
- контрава-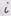 :
: 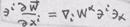 В новой системе координат левая часть равенства равна:
В новой системе координат левая часть равенства равна:
 . Следовательно,
. Следовательно, 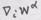 компоненты тензора.
компоненты тензора.


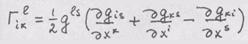 . I
. I
 , поэтому
, поэтому
 , Складывая выражение
, Складывая выражение
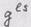 и образуя сверт-
и образуя сверт- (неверно: сокращая на
(неверно: сокращая на 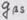 ), получим искомую
), получим искомую и
и  ,
,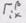 в случае сферической си-
в случае сферической си-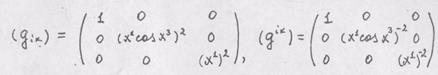
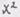 . Поэтому
. Поэтому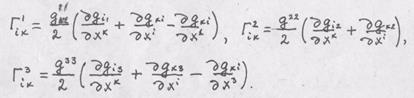
 Ответ.
Ответ.
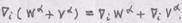

 в цилиндрической системе координат.
в цилиндрической системе координат.
 (набла), где
(набла), где
 - обозначение ковариантной производной. п.1. Оператор "градиент" (),
- обозначение ковариантной производной. п.1. Оператор "градиент" (), 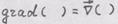
 - скалярная функция
- скалярная функция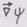 - вектор, и определить его
- вектор, и определить его
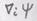 - ковариантные компоненты вектора
- ковариантные компоненты вектора 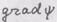 Задача 2. Найти компоненты
Задача 2. Найти компоненты 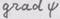 в декартовой
в декартовой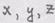 ; здесь
; здесь 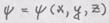
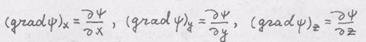
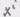
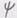 скалярная функция, то ковариантная
скалярная функция, то ковариантная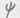 совпадает с частной, при
совпадает с частной, при
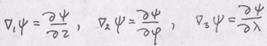
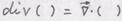 Применяется к тензорным величинам ранга больше нуля. Задача 4. Выразить
Применяется к тензорным величинам ранга больше нуля. Задача 4. Выразить 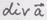
 - вектор, в декартовых
- вектор, в декартовых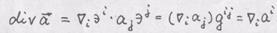
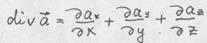
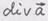 ,
,  - вектор, в случае
- вектор, в случае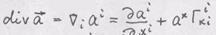
 вычисляется по формуле
вычисляется по формуле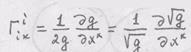
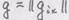

 нет).
нет). 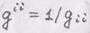
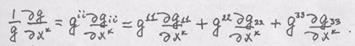
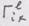 в случае той же системы равно
в случае той же системы равно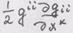

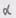 , получим искомое.
, получим искомое.


