ЗАНЯТИЕ 1
НАЗНАЧЕНИЕ 2
ТЕХНИЧЕСКИЕ ДАННЫЕ 3
УСТРОЙСТВО И РАБОТА ИЗДЕЛИЯ 14 Принцип действия 14
ПОДГОТОВКА К РАБОТЕ 18 1. Расположение органов управления 19 2. Подготовка к измерениям 21 3. Проверка работоспособности 21
ПОРЯДОК РАБОТЫ 23 1. Отсчет показаний и погрешности измерений 23 2. Порядок выключения прибора 23 3. Измерение частоты по входу А 23 4. Измерение частоты по входу Б 24 5. Измерение периода 25 6. Измерение интервалов времени 26 7. Измерение длительности импульсов 28 8. Измерение отношения частот 28 9. Работа прибора при внешнем пуске автоматики 29 10. Работа прибора в качестве источника кварцованных частот 29 11. Работа прибора с внешним стандартом частоты 30
ЗАНЯТИЕ 1 Тема. ЭЛЕМЕНТЫ ТЕНЗОРНОГО ИСЧИСЛЕНИЯ. КРИВОЛИНЕЙНЫЕ КООРДИНАТЫ. БАЗИСНЫЕ ВЕКТОРЫ. СОГЛАШЕНИЕ О СУММИРОВАНИИ. МЕТРИЧЕСКАЯ МАТРИЦА.
п.1. Криволинейные координаты изучаются на примере сферической системы координат Координатной поверхностью Координатной линией называют геометрическое место точек, для которых одна и только одна координата переменна. Координатные линии – пересечения координатных поверхностей. Задача 1. Определить координатные поверхности введенной сферической системы координат, проходящие через точку М. Ответ. Координатная поверхность Задача 2. Определить координатные линии введенной сферической системы координат, проходящие через точку М. Ответ. Координатная линия п.2. Базисные векторы
направлены по касательным к координатным линиям в точке М в сторону возрастания соответствующей кооординаты (индексы Задача 3. Показать, что касательные к координатным линиям в точке М введенной сферической системы координат взаимно перпендикулярны. Ответ. Касательные лежат во взаимно перпендикулярных плоскостях, следовательно, они взаимно перпендикулярны. (Полезно доказать также с использованием теоремы о трех перпендикулярах). Задача 4. Определить модули векторов базиса введенной сферической системы координат в точке М. Решение. Величина
В зависимости от положения точки М изменяются, вообще говоря, направления и величины базисных векторов. п.3. Соглашение о суммировании (введено А.Эйнштейном) по немым индексам (один из них, ковариантный, расположен снизу индексируемой величины, а другой, контравариантный, сверху) означает, что Упражнения. Дать развернутую запись 1. Если 2. 3. 4. Разложим вектор п.4. Метрическая матрица позволяет выразить квадрат расстояния между M и N в виде:
Матрица из коэффициентов Упражнение. Дать развернутую запись Ответ:
Задача 5. Найти компоненты Решение. Запишем выражение длины внутренней диагонали прямоугольного параллелепипеда, сторонами которого являются Тогда
Это симметричная матрица с нулевыми недиагональными элементами, что характерно для рассматриваемой ортогональной системы координат. п.5. Сопряженной матрицей или обратной к матрице метрической
где Задача 6. Найти матрицу, обратную к матрице метрической в точке M, введенной сферической системы координат. Решение. Так как
то искомая обратная матрица имеет виц:
п.6. Сопряженный (обратный, контравариантный) базис векторов
Задача 7. Найти разложение базисных векторов Решение: Дополнительные задачи. 1. Решить задачи 1-7 в случае цилиндрической системы координат. 2. Доказать, что 3. Доказать, что 4. Доказать, что 5. Упростить выражения 6. Упростить выражение 7. Вычислить
|

 (рис,1). Используем обозначения
(рис,1). Используем обозначения  .
. называют геометрическое место точек, для которых указанная координата постоянна. Например, в координатной плоскости
называют геометрическое место точек, для которых указанная координата постоянна. Например, в координатной плоскости  декартовой прямолинейной системы координата
декартовой прямолинейной системы координата  ее точек постоянна и равна нулю.
ее точек постоянна и равна нулю. – сфера радиуса
– сфера радиуса  с центром в точке
с центром в точке  ; координатная поверхность
; координатная поверхность  – полуплоскость, проходящая через ось
– полуплоскость, проходящая через ось  и точку М; координатная поверхность
и точку М; координатная поверхность  – коническая поверхность, ось симметрии которой –
– коническая поверхность, ось симметрии которой –  .Поверхности указаны на рис.2.
.Поверхности указаны на рис.2. – луч, проходящий через
– луч, проходящий через  ; координатная линия
; координатная линия  – окружность радиуса
– окружность радиуса  , плоскость которой параллельна
, плоскость которой параллельна  ; координатная линия
; координатная линия  – полуокружность радиуса
– полуокружность радиуса 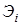 (или векторы базиса) по определению равны
(или векторы базиса) по определению равны
 могут принимать значения 1, 2, 3 и расположены в циклическом порядке). Концы векторов, стоящих в числителе дроби, лежат на координатной линии
могут принимать значения 1, 2, 3 и расположены в циклическом порядке). Концы векторов, стоящих в числителе дроби, лежат на координатной линии  .
. , здесь
, здесь  , где M и N - точки, лежащие на координатной линии
, где M и N - точки, лежащие на координатной линии  ,
, .
.


 Немые индексы можно обозначать различными буквами.
Немые индексы можно обозначать различными буквами. Ответ:
Ответ:  , индекс
, индекс  – свободный (по нему нет суммирования).
– свободный (по нему нет суммирования). – символ Кронекера, то
– символ Кронекера, то  .
. Ответ:
Ответ: 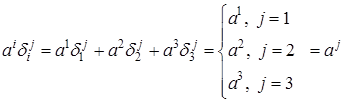 .
. Ответ:
Ответ:  .
. Ответ:
Ответ:  .
. , соединяющий пару бесконечно близких точек M и N, по направлениям базисных векторов в точке M.
, соединяющий пару бесконечно близких точек M и N, по направлениям базисных векторов в точке M.  .
. .
. называется метрической. Первый индекс означает номер строки, второй – столбца.
называется метрической. Первый индекс означает номер строки, второй – столбца. .
.
 в точке M в случае введенной сферической системы.
в точке M в случае введенной сферической системы. ,
,  ,
,  .
. . Сравнивая полученное соотношение с раскрытым выше выражением, получаем матрицу:
. Сравнивая полученное соотношение с раскрытым выше выражением, получаем матрицу:
 называется матрица
называется матрица  , если элементы этих двух матриц связаны следующим образом:
, если элементы этих двух матриц связаны следующим образом: или
или  ,
, – элементы транспонированной матрицы
– элементы транспонированной матрицы  ;
;  – алгебраическое дополнение к элементу
– алгебраическое дополнение к элементу  ,
,  – определитель матрицы
– определитель матрицы  ,
,  – миноры к элементу
– миноры к элементу  ,
, ,
, .Элементы матриц определены при
.Элементы матриц определены при  .
.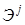 определяется выражением:
определяется выражением:
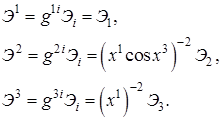
 .
. .
. .
. .
. , если
, если  .
. ,
,  .
.


