Фракталы и фракталоподобные структуры
Фракталы это уже теперь не мода в науке, а общая банальная проза жизни. Фракталоподобными структурами называют такие, у которых вид при разном масштабе напоминает друг друга. Например, вид береговой линии, колебания дробового (электронного) шума в электрических цепях и измерительных приборах, биржевые тренды и т.д. Математические фрактальные структуры в некоторых своих масштабах имеют полное, как правило, подобие самим себе, в силу способа построения. Например, возьмем отрезок и построим на его основе кривую из четырех отрезков. Потом на каждом из этих отрезков еще такие же кривые. И еще. До бесконечности повторив последовательную процедуру, получим триадную кривую Коха. Если исходной фигурой будет внешний контур шестиконечной звезды, а дальше на каждом ребре до бесконечности будет строиться такой же, как раньше, то получиться «снежинка» Коха. Кривая Коха «Снежинка» Коха
«Снежинка» Коха не может служить частью более крупной фрактальной структуры, кривая – может. Из других исскуственно-математических структур чаще всего называют ковры Серпинского и множество Мандельброта.
В музыке при изменении частоты колебания звука в два раза начинается новая октава. Полуоктава – это изменение частоты в Ф – 1 =1/Ф = ( Возьмем степени чисел Ф и
Если мы изобразим эти степени в логарифмической шкале, то получим 2 равномерные шкалы, наложенные друг на друга (рис. 2). В часть интервалов
[n, n+1] внутрь будут попадать числа m, в часть – нет. Эти последние – заштрихуем. Попадание на границу – считаем непопаданием внутрь. Если мы изобразим эти шкалы дважды повторенными и замкнутыми по кругу получим рис.41. Эта математическая структура – теоретическая основа понятия «7 тонких тел» и 12(16) каналов между ними. Т. к. выражение Ф18
Этот рис., кстати, дает картинку близкую к виду октавы на клавиатуре фортепиано:
|


 12. Математические основания схемы «12х14»
12. Математические основания схемы «12х14»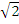 раз. Золотое сечение – это разбиение интервала на отрезки так, чтобы отношение всего отрезка к большей доле было равно отношению большей доли к меньшей. Число золотого сечения Ф = (1 +
раз. Золотое сечение – это разбиение интервала на отрезки так, чтобы отношение всего отрезка к большей доле было равно отношению большей доли к меньшей. Число золотого сечения Ф = (1 +  )/2 = 1,618…,
)/2 = 1,618…,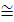 (
(




