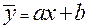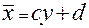КРИТЕРИЙ ФИШЕРА
Для сравнения двух нормально распределенных совокупностей, у которых нет различий в средних выборочных значениях, но есть разница в дисперсиях, используют критерий Фишера. Фактический критерий рассчитывают по формуле:
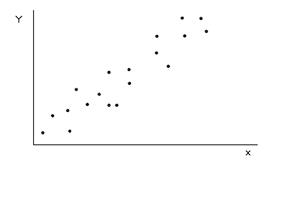
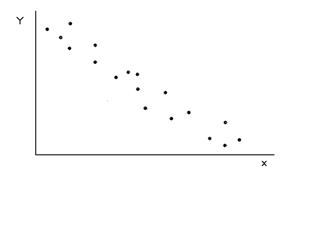
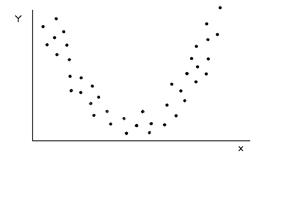
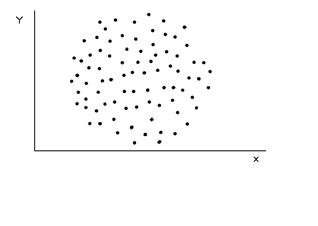
где в числителе стоит большее значение выборочной дисперсии, а в знаменателе - меньшее. Для вывода о достоверности различий между выборками используют ОСНОВНОЙ ПРИНЦИП проверки статистических гипотез. Критические точки для П р и м е р: при изучении влияния некоторого препарата на скорость проростания семян было установлено, что в экспериментальной партии семян и контроле средняя скорость проростания одинакова, но есть разница в дисперсиях. КОРРЕЛЯЦИОННАЯ ЗАВИСИМОСТЬ. КОЭФФИЦИЕНТ КОРРЕЛЯЦИИ И ЕГО СВОЙСТВА. УРАВНЕНИЯ РЕГРЕССИИ. ЗАДАЧА корреляционного анализа сводится к: 1. Установлению направления и формы связи между признаками; 2. Измерению ее тесноты. Функциональной называется однозначная зависимость между переменными величинами, когда определенному значению одной (независимой) переменной х, называемой аргументом, соответствует определенное значение другой (зависимой) переменной у, называемой функцией. (Пример: зависимость скорости химической реакции от температуры; зависимость силы притяжения от масс притягивающихся тел и расстояния между ними). Корреляционной называется зависимость между переменными, имеющими статистистический характер, когда определенному значению одного признака (рассматриваемого в качестве независимой переменной) соответствует целый ряд числовых значений другого признака. (Пример: связь между урожаем и количеством осадков; между ростом и весом и т.д.). Поле корреляции представляет собой множество точек, координаты которых равны полученным на опыте парам значений переменных х и у. По виду корреляционного поля можно судить о наличии или отсутствии связи и ее типе.
Связь называется положительной, если при увеличении одной переменной увеличивается другая переменная. Связь называется отрицательной, если при увеличении одной переменной уменьшается другая переменная. Связь называется линейной, если ее можно в аналитическом виде представить как Показателем тесноты связи является коэффициент корреляции. Эмпирический коэффициент корреляции определяется выражением:
Коэффициент корреляции лежит в пределах от -1 до 1 и характеризует степень близости между величинами x и y. Если: 1. 2. 3. 4. 5. 6. 7. Корреляционную зависимость между признаками можно описывать разными способами. В частности, любая форма связи может быть выражена уравнением общего вида
Уравнение прямой регрессии х на у в общем случае выглядит как
Наиболее вероятные значения коэффициентов а и в, с и d могут быть вычислены, например, при использовании метода наименьших квадратов.
|

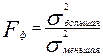
 содержатся в таблице. Нулевую гипотезу отвергают, если фактически установленная величина
содержатся в таблице. Нулевую гипотезу отвергают, если фактически установленная величина 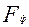 превзойдет или окажется равной критическому (стандартному) значению
превзойдет или окажется равной критическому (стандартному) значению 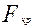 этой величины для принятого уровня значимости a и числа степеней свободы k1=nбольшая-1; k2=nменьшая-1.
этой величины для принятого уровня значимости a и числа степеней свободы k1=nбольшая-1; k2=nменьшая-1.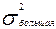 =1250,
=1250, 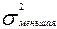 =417. Объемы выборок одинаковы и равны 20.
=417. Объемы выборок одинаковы и равны 20. 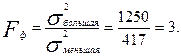
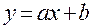 .
.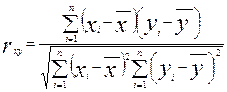
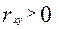 - положительная корреляция;
- положительная корреляция;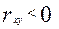 - отрицательная корреляция;
- отрицательная корреляция;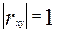 - связь функциональная;
- связь функциональная;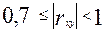 - связь высокая (или сильная);
- связь высокая (или сильная);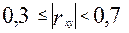 - связь средняя;
- связь средняя;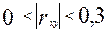 - связь слабая;
- связь слабая;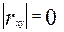 - связи нет.
- связи нет.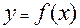 . Уравнение вида
. Уравнение вида 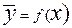 и
и 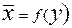 называются регрессией. Уравнение прямой регрессии у на х в общем случае можно записать в виде
называются регрессией. Уравнение прямой регрессии у на х в общем случае можно записать в виде