Упражнения. 5.50. Определить угловую скорость вращения ω коленчатого вала двухвального клавишного соломотряса
5.50. Определить угловую скорость вращения ω; коленчатого вала двухвального клавишного соломотряса, имеющего радиус кривошипа r и показатель кинематического режима k.
5.51. Определить фазу отрыва ωt1 соломы от поверхности двухвального соломотряса, если угол наклона рабочей поверхности к горизонту α;, радиус кривошипа коленчатого вала r и он вращается с угловой скоростью ω;.
5.52. Определить фазу отрыва ωt1 соломы от поверхности двухвального соломотряса, имеющего угол наклона к горизонту α;, если показатель кинематического режима k.
5.53. Определить показаетль кинематического режима двухвального соломотряса, если радиус кривошипа коленчатого вала r и он вращается с угловой скоростью ω;.
5.54. Рабочая поверхность двухвального клавишного соломотряса наклонена под углом α; к горизонту. Коленчатый вал имеет радиус кривошипа r и вращается с угловой скоростью ω;. Принимая длительность отдельных соударений ничтожно малой, определить момент t 1 отрыва соломы от поверхности клавиши соломотряса.
5.55. Будет ли двухвальный клавишный соломотряс перемещать соломистый ворох в копнитель, если его рабочая поверхность наклона под углом α; к горизонтали, а коленчатый вал имеет радиус кривошипа r и вращается с угловой скоростью ω;.
5.56. Определить показатель режима работы k горизонтального клавишного соломотряса для случая, когда солома, подброшенная одной группой клавиш, падает сразу на обе группы. Радиус кривошипа коленчатого вала r = 0,04 м, а ωt3 = π;. 5.57. Доказать, что 5.58. Доказать, что 5.59. Доказать, что 5.60. Определить срднюю скорость перемещения соломы по соломотрясу, если поазатель режима работы k = 1,0, радиус кривошипа коленчатого вала r = 0,05 м, а угол наклона клавиш α; = 0.
4.6. МАШИНЫ ДЛЯ ПОСЛЕУБОРОЧНОЙ ОБРАБОТКИ ЗЕРНА
4.6.1. Размерные характеристики семян. Работа плоских решет
Всякая зерновая смесь может быть разделена на составные части при условии, если эти части отличаются друг от друга по своим физико-механическим свойствам. Наиболее важными физико-механическими свойствами, используемыми при очистке и сортировании зерна являются: геометрические размеры, аэродинамические свойства, форма и состояние поверхности, плотность и удельная масса, электропроводность, цвет. При подборе средств механизации очистки и сортирования семян нельзя пользоваться только средними показателями их физико-механических свойств, так как семена, даже выращенные в одних условиях, отличаются большой изменчивостью. Показателем изменчивости того или иного размера семян во всей их совокупности служит вариационный ряд или вариационная кривая, составленная путем массового измерения данного вида семян. В результате замеров, например, устанавливают наименьшую lmin и наибольшую lmax длину. Разность lmax–lmin делят на классовый промежуток λ; (мм). Для хлебных зерен λ; принимают равным 0,2; 0,25; 0,3 и 0,4 мм. Тогда число классов:
Как показали опыты, изменение размеров сортируемых материалов в большинстве случаев подчиняется закону нормального распределения. При нормальном распределении размерных характеристик в пределах Мср±3σ; заключено 99,7 % всего количества материала, т.е можно принять, что размеры материала изменяются
где Мср – среднее арифметическое значение вариационного ряда; σ; – среднеквадратичное отклонение, мм. Среднеарифметическую вариационного ряда находят по формуле:
а среднеквадратическое отклонение – по выражению:
где mi – частота (количество семян в i -ом классе), шт.; li – среднее значение класса, мм. Таким образом, по вариационным рядам и кривым, характеризующим изменение замеренного размера сортируемого материала, устанавливают, по какому признаку можно разделять смеси, и определяют последовательность операций. В соответствии с типом решета рабочие размеры отверстий а могут быть приближенно рассчитаны по выражениям: для колосовых решет ак ≥ Мср + 3σ, (4.120) для подсевных решет ап ≈ Мср – 2σ... Мср – 1,5σ;, (4.121) для сортировальных решет, дающих второй сорт, ас ≈ Мср–σ;. (4.122) Определенные по формулам (4.120), (4.121) и (4.122) рабочие размеры отверстий решет округляют до большего ближайшего значения согласно ГОСТ 214-57. ГОСТ 214-57 предусматривает: решеты с круглыми отверстиями (размеры в мм): 0,8; 0,9; 1,0; 1,1; 1,2; 1,3; 1,4; 1,5; 1,6; 1,7; 1,8; 1,9; 2,0; 2,1; 2,25; 2,5; 2,6; 2,75; 3,0; 3,25; 3,5; 3,75; 4,0; 4,25; 4,5; 4,75; 5,0; 5,25; 5,5; 6,0; 6,5; 7,0; 7,5; 8,0; 9,0; 9,5; 10,0; 10,5; 11,0; 12,0; 13,0; 14,0; 15,0; 16,0; 18,0; 20,0; 22,0; 24,0; 26,0; 28,0; 30,0; 35,0; 40,0; решеты с продолговатыми отверстиями (размеры в мм): 0,5; 0,6; 0,7; 0,8; 0,9; 1,0; 1,1; 1,2; 1,3; 1,4; 1,5; 1,6; 1,7; 1,8; 1,9; 2,0; 2,2; 2,4; 2,6; 2,8; 3,0; 3,25; 3,5; 3,65; 4,0; 4,25; 4,5; 4,75; 5,0; 5,25; 5,5; 5,75; 6,0; 6,5; 7,0; 7,5; 8,0; 9,0; 10,0. Производительность решет определяют по удельной нагрузке на единицу площади:
где Q – производительность решет, кг/с; S – площадь решета, м2; k – коэффициент, зависящий от вида обрабатываемой культуры и равный для пшеницы 1; для ржи, ячменя, гороха и кукурузы – 0,75; для овса, риса, фасоли и гречихи – 0,55; для клевера и люцерны – 0,2; qs – допустимая удельная нагрузка на решето (таблица 4.8), кг/(м2·с):
Таблица 4.8 – Допустимая удельная нагрузка на решето qs, кг/м2·с [2,7,9,10 ]
Ускорение решет или отношение его максимального значения ω2r к ускорению свободного падения g является показателем кинематического режима работы решета
где r – радиус кривошипа, приводящего в движение решето (амплитуда колебания), м; ω; – угловая скорость кривошипа, рад/с. Различают следующие виды относительного движения материала по поверхности решета: Перемещение материала вверх
перемещение материала вниз
отрыв материала
где α – угол наклона плоскости решета к горизонту, град; ε; – угол, характеризующий направленность колебаний решета (угол между направлением колебаний и горизонтальной плоскостью), град; φ; – угол трении частиц материала о поверхность решета.
Пример 116. Определить число и границы классов для построения кривых распределения семян пшеницы, если при массовом измереннии размеров семян пшеницы получено: длина Мср = 6,43 мм, σ; = ± 0,65 мм; ширина Мср = 2,95 мм, σ; = ±0,33 мм; толщина Мср = 2,71 мм, σ; = ±0,33 мм. Решение: Составлять распределения семян по слишком большому количеству классов практически нецелесообразно. Можно ограничиться 5...6 классами и не свыше 11...13 классов. Для упрощения вычислительной работы величину классового промежутка, а также границы классов удобнее выбирать четными. Из выражений (4.117):
то при классовом промежутке λ; можно ограничиться n классами. Длина семян: Мср = 6,43 мм; σ; = ± 0,65 мм.
При классовом промежутке λ; = 0,4 мм число классов по выражению (4.116):
Установим границу классов. Минимальный размер
Пусть крайняя граница 1-го класса равна 4,40 мм, тогда другая граница 1-го класса будет равна 4,40 + λ = 4,40 + 0,4 = 4,80 мм. Все границы последующих классов определяются прибавлением к 4,40 мм значений 2 λ;, 3 λ;,... 10 λ;. Крайние границы последнего, 10-го, класса будут: 4,40 + 9·0,4 = 8,0 мм 4,40 + 10·0,4 = 8,40 мм. Максимальная длина семян
Отсюда следует, что и наиболее длинные зерна пшеницы помещаются в пределах 10 класса. Аналогично определим для ширины семян: n = 11 при λ; = 0,2 мм, границы 1-го класса 1,8 мм и 2,0 мм; границы 11-го класса 3,8 мм и 4,0 мм. Аналогично определим для толщины семян: n = 11 при λ; = 0,2 мм, границы 1-го класса 1,6 мм и 1,8 мм; границы 11-го класса 3,6 мм и 3,8 мм. Ответ: длина: n = 10; λ; = 0,4 мм; границы 1-го класса 4,4 мм и 4,8 мм, границы 10-го класса 8,0 мм и 8,4 мм; ширина: n = 11; λ; = 0,2 мм; границы 1-го класса 1,8 мм и 2,0 мм; границы 11-го класса 3,8 мм и 4,0 мм; толщина: n = 11; λ; = 0,2 мм; границы 1-го класса 1,6 мм и 1,8 мм; границы 11-го класса 3,6 мм и 3,8 мм.
Пример 117. Построить вариационную кривую, определить среднее значение вариационного ряда Мср и среднеквадратическое отклонение для зерен пшеницы по ширине. Данные промера ширины 300 шт. зерен дали следующее их распределение:
Решение: Согласно формуле (4.118) среднеарифметическаяое значение вариационного ряда:
а среднеквадратическое отклонение по выражению (4.119):
Количество зерен m в каждом классе выразим в процентах (Р) от общего количества N измеренных зерен и тогда получим вариационный ряд:
Аналогично Р3 = 26%; Р4 = 35,5%; Р5 = 20%; Р6 = 4,3% Для построения вариационной кривой откладываем по оси абсцисс линейные размеры, а по оси ординат – количество зерен в процентах, причем количество зерен в каждом из классов относим к среднему линейному размеру данного класса (см. рисунок 4.30)
Рисунок 4.30 - Вариационная кривая изменчивости ширины зерен пшеницы
Ответ: Мср = 2,87 мм; σ; = 0,63 мм.
Пример 118. Определить рабочий размер отверстий колосового решета при разделении семян пшеницы от крупных примесей, если среднее значение вариационного ряда Мср = 2,81 мм, и среднеквадратическое отклонение σ; = 0,37 мм получены при массовом замере толщины семян пшеницы. Решение: Разделение семян по толщине осуществляется на решетах с продолговатыми отверстиями, так как сквозь продолговатое отверстие может пройти только такое зерно, толщина которого меньше ширины щели отверстия. Длина зерна не имеет значения, она всегда меньше длины продолговатого отверстия, а ширина зерна всегда больше толщины, то зерно, которое не проходит сквозь продолговатое отверстие по толщине, тем более не пройдет по ширине. Согласно выражению (4.120) рабочий размер продолговатых отверстий для колосовых решений ак ≥ Мср + 3σ = 2,81 + 3·0,37 = 3,92 мм. Согласно ГОСТ 214-57 выбираем решето с продолговатыми отверстиями ак = 4,0 мм. Ответ: 4,0 мм. Пример 119. Определить производительность решета при предварительной очистке семян ржи, если решето, установленное на ОВС-25, имеет следующие размеры: длину 1000 мм, а ширину – 800 мм. Решение: Производительность решета определяем по формуле (4.123). Коэффициент k при очистке ржи равен 0,75. Допустимая удельная нагрузка при предварительной очистке семян ржи колеблется в пределах 1,33...1,54 кг/(м2·с). Поэтому
Ответ: 0,79...0,92 кг/с.
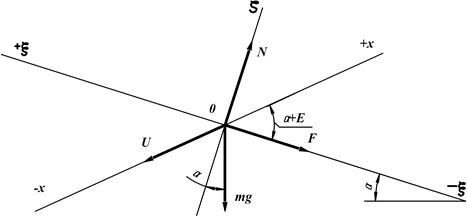
Пример 120. Установить возможные виды относительного движения материала по поверхности решета зерноочистительной машины с параметрами: α; = 6°, ε; = 29°, φ; = 25°, r = 10 мм, n = 325 мин-1. Решение сопроводить расчетной схемой. Решение: Рассмотрим расченую схему (рисунок 4.31)
Рисунок 4.31 – Силы, действующие на частицу, находящуюся на наклонной колеблющейся плоскости (движение частицы вверх по плоскости)
Для решения задачи примем следующие допущения. 1. Зерновой материал движется, как плоская частица. 2. Сопротивление воздуха не оказывает существенного влияния на движение материала. 3. Коэффициент f сопротивления перемещению материала не зависит от толщины его слоя и кинематических факторов. На частицу массой m, расположенную на наклонной плоскости ξ-ξ;, действует сила тяжести mg, сила инерции U =m∙; ω; 2∙r∙cosωt, реакция N и сила трения F = N ∙tgφ;. Дифференциальные уравнения движения материальной точки с массой m относительно плоскости решета имеют вид
Пока N ≥0, частица находится на плоскости и, следовательно, ζ= 0. Поэтому
Подставив значение N из (2) в первое уравнение системы (1) и после некоторых преобразований, получим
где Движение частицы вверх возможно, если правая часть уравнения (3) больше нуля, т.е.:
При cos ωt =1, неравенство (4) примет вид
Определим величину где Численное значение К1 определится из выражения (5)
Поскольку К>К1, т.е. 1,18>1,03, то будут наблюдаться сдвиги материала вверх по решету. Приведем расчетную схему (рисунок 4.32). Аналогично рассмотрев расчетную схему (рисунок 4.32), получим
где
Рисунок 4.32 - Силы, действующие на частицу, находящуюся на наклонной колеблющейся плоскости (движение частицы вниз по плоскости)
Движение частицы вниз возможно, если правая часть уравнения (6) больше нуля, т.е.:
При cos ωt =1, неравенство (7) примет вид
Определим численное значение К2 по выражению (8)
Поскольку К>К2, то будет происходить движение материал вниз по решету. Отрыв материала от поверхности решета возможен при N =0 (см. рисунок 4.31 и 4.32):
Отсюда при cos ωt =1
Определим численное значение К0 по выражению (10)
Поскольку численное значение К<К0, то отрыва материала от поверхности решета не будет. Таким образом, при работе решета будут наблюдаться сдвиги материала вверх и вниз по решету без отрыва от поверхности. Преимущественное движение материала вниз. Ответ: К = 1,18; К1 = 1,03; К2 = 0,33; К0 = 1,74; К0 > К > К1 > К2.
|

 . Доказательство сопроводить расчетной схемой.
. Доказательство сопроводить расчетной схемой. . Доказательство сопроводить расчетной схемой.
. Доказательство сопроводить расчетной схемой. . Доказательство сопроводить расчетной схемой.
. Доказательство сопроводить расчетной схемой. (4.116)
(4.116) , (4.117)
, (4.117) (4.118)
(4.118) (4.119)
(4.119) (4.123)
(4.123) , (4.124)
, (4.124)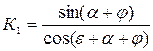 ; (4.125)
; (4.125)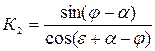 ; (4.126)
; (4.126) ; (4.127)
; (4.127)
 мм.
мм. классов.
классов. мм.
мм. мм.
мм.
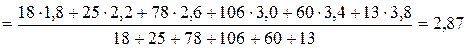 мм,
мм,

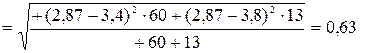 мм.
мм.



 (1)
(1) . (2)
. (2) , (3)
, (3) .
. . (4)
. (4) . (5)
. (5) ,
, рад/с.
рад/с.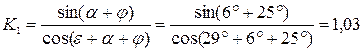 .
. , (6)
, (6) .
.
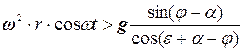 . (7)
. (7) . (8)
. (8) .
. . (9)
. (9) . (10)
. (10)



