Метод наименьших квадратов.
Саратовский государственный технический университет
Пусть на основании эксперимента необходимо установить функциональную зависимость между двумя переменными величинами х и у.
Пусть, например точки взятые из таблицы 1 расположены так, как на рис.1. В данном случае естественно предположить, что между х и у, существует линейная зависимость выражаемая формулой ax+b. Подставляя значения координат точек в выражение у-(ax+b) получим равенство:
Поставим задачу подобрать коэффициенты а и b таким образом, чтобы эти погрешности были возможно меньше по абсолютной величине. Для этого рассмотрим сумму квадратов погрешностей.
Параметры a,b будем находить из условия минимума S(a,b). Находим первый частные производные по параметрам a и b.
Приравняем частные производные к 0. Получим линейную систему с двумя уравнениями a и b.
Система 2 называется нормальной системой метода наименьших квадратов. Решая систему 2, находим a и b. И затем подставляем их в (1) получаем уравнение искомой прямой. Тот факт, что S(a,b) в т. M(a;b) имеем минимум и легко устанавливается с помощью частных производных 2 порядка. Пример: В результате эксперимента получены 5 значении искомой функции y. При 5 значениях аргумента
Решение: Будем искать функциональную зависимость между х и у в виде линейной функции ax+b
a=0,425 2,125+5b=8 b=1,175 Ответ: у=0б425х+1,175 В случае нахождения приближающей функции в виде квадратного трехчлена
Находим
Решение системы (4) дает значение параметров a,b,c для приближающей функции (3). В качестве приближающих функций в зависимости от характера точечного графика f часто используются следующие функции: 1) 2) 3) 4) 5) 6) 7) 8) Здесь a,b,c,m параметры. Когда вид приближающей функции установлен, задача сводится только к отысканию значений параметров. Нахождение приближающей функции в виде других элементарных функций. Покажем, как нахождение приближающей функции с 2мя параметрами в виде элементарных функций 1-8 может быть сведено к нахождению параметров линейной функции. Будем искать приближающую функцию в виде:
Учитывая, что в исходной таблице 1 значения аргумента и значения функции положительны прологарифмируем равенство (5) при условии
Так как F приближающая функция для f, функция lnF будет приближающей для функции lnf. Введем новую переменную u=lnx, функцией от u: Φ(u)
Тогда (6) примет вид: То есть задача свелась к отысканию приближающей функции в виде линейной. Для нахождения приближающей функции в виде степенной при сделанных выше предположениях, выполним следующее: - по новой таблице найти параметры A и B по функции вида (8). - используя обозначения (7) найти значения параметров a и m и поставить их в (5). Замечание: значения разностей
Для найденной имперической функции (B) в соответствии с исходной таблицей 1, можно найти сумму квадратов отклонений
Пример: Построить приближающую функцию методом наименьших квадратов для зависимости заданной следующей таблицей:
Для сравнения качества приближений рассмотреть 2 способа приближений к заданной функции: в виде прямой ax+b и в виде смешенной функции y=Cxm После нахождения значений параметров а и b, с и m, найти сумму квадратов отклонений (В) и установить какое из 2х приближений лучше. Решение Пологая, что х,у связаны зависимостью вида
Получим систему вида:
5b=36-30a; b=-1,006. a=0,932.
Тогда получим: y=0,932x-1,006 Прологарифмируем данные
Решаем как систему линейного уравнения
а = 11,86* -18,32b=25,65 b=-1,4. Тогда a=1,69
m= a =1,69 ln(c)=b, c=0,247; y=cxm=0,247x1,69 Относительная ошибка: 1) y=0,932x-1,006
Ɛ1=0,2808 Ɛ3=0,1308 Ɛ4=-0,09 Ɛ5=0,1424 Ɛ6=0,188 Ɛ7=0,0528 Ɛ8=0,02 ПогрешностьS(a,b)= 2) y=0,247x1,69
Ɛ1=0,1 Ɛ3=0,2 Ɛ4=0,2 Ɛ5=0,1 Ɛ6=-0,1 Ɛ7=0 Ɛ8=-0,2 S(a,b)=σ22=0,3 Первое приближение лучше, так как σ1 <σ2
|











 Таблица 1
Таблица 1
 -погрешности.
-погрешности.







 ;
; 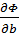 ;
;  и приравниваем к 0.
и приравниваем к 0.
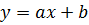


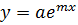





 :
:
 , lna=B. (7)
, lna=B. (7) (8)
(8) (A); i=1,2,…,n называются отклонениями значения y вычисленных по формуле
(A); i=1,2,…,n называются отклонениями значения y вычисленных по формуле (B)
(B) , которая в соответствии с методом наименьших квадратов для заданного вида приближающей функции должна быть наименьшей из 2х различных приближений одной и той же табличной функции следуя принципу наименьших квадратов лучшим нужно считать, для которого сумма B имеет наименьшее значение.
, которая в соответствии с методом наименьших квадратов для заданного вида приближающей функции должна быть наименьшей из 2х различных приближений одной и той же табличной функции следуя принципу наименьших квадратов лучшим нужно считать, для которого сумма B имеет наименьшее значение.



 σ12=0,203
σ12=0,203


