Куски 14)
Язык SDL предназнечена для… Описания процессов установления соединений Язык Ассемблера… Машинно-ориентированный Язык MML используют для… Организации диалога оператора с электронной управляющей машиной Является ли канал ввода и вывода специализированным да Язык программирования приближенный к системе команд конкретного микропроцессора – это… Ассемблер Язык программирования в системе DTS–3100 C++, CHILL, Ассемблер 11. Процесс теплообмена между поверхностью тела и средой описывается законом Ньютона-Рихмана, которая гласит, что тепловой поток, передаваемый конвективным теплообменом прямо пропорционально разности температур поверхности тела (t'ст) и окружающей среды (t'ж): Q = α · (t'ст - t'ж)·F, (10.1) или q = α · (t'ст - t'ж), (10.2) где: коэффициент теплоотдачи [Вт/(м2К)], характеризует интенсивность теплообмена между поверхностью тела и окружающей средой.
Факторы, которые влияют на процесс конвективного теплообмена, включают в этот коэффициент теплоотдачи. Тогда коэффициент теплоотдачи является функцией этих параметров и можно записать эту зависимость в виде следующего уравнения: α = f1(Х; Ф; lo; xc; yc; zc; wo; θ; λ; а; ср; ρ; ν; β), (10.3) где: Х – характер движения среды (свободная, вынужденная); Ф – форма поверхности; lo – характерный размер поверхности (длина, высота, диаметр и т.д.); xc; yc; zc – координаты; wo – скорость среды (жидкость, газ); θ = (t'ст - t'ж) – температурный напор; λ – коэффициент теплопроводности среды; а – коэффициент температуропроводности среды; ср –изобарная удельная теплоемкость среды; ρ –плотность среды; ν – коэффициент кинематической вязкости среды; β – температурный коэффициент объемного расширения среды.
Уравнение (10.3) показывает, что коэффициент теплоотдачи величина сложная и для её определения невозможно дать общую формулу. Поэтому для определения коэффициента теплоотдачи применяют экспериментальный метод исследования.
Достоинством экспериментального метода является: достоверность получаемых результатов; основное внимание можно сосредоточить на изучении величин, представляющих наибольший практический интерес.
Основным недостатком этого метода является, что результаты данного эксперимента не могут быть использованы, применительно к другому явлению, которое в деталях отличается от изученного. Поэтому выводы, сделанные на основании анализа результатов данного экспериментального исследования, не допускают распространения их на другие явления. Следовательно, при экспериментальном методе исследования каждый конкретный случай должен служить самостоятельным объектом изучения.
12. Уравнение энергии. Выведем дифференциальное уравнение, описывающее температурное поле в движущейся жидкости. При выводе будем полагать, что жидкость однородна и изотропна, ее физические параметры постоянны, энергия деформации мала по сравнению с изменением внутренней энергии.
Рис. 4.3. К выводу дифференциального уравнения энергии. Выделим в потоке жидкости неподвижный относительно координатной системы элементарный параллелепипед (рис. 4.3) с ребрами dx, dy и dz. Через грани параллелепипеда теплота переносится теплопроводностью и конвекцией; в общем случае в рассматриваемом объеме может выделяться теплота внутренними источниками за счет энергии, внешней по отношению к рассматриваемой жидкости. Вывод уравнения энергии, соответствующего принятым здесь условиям, уже рассматривался в § 1.6. Было получено уравнение (1.25), где
Уравнения движения. Вывод дифференциального уравнения движения вязкой жидкости требует громоздких математических выкладок. В связи с этим будет дан упрощенный вывод этого уравнения для случая одномерного течения несжимаемой жидкости. Этот вывод не является строгим, его основное достоинство заключается в наглядности. Для трехмерного движения уравнение будет приведено без вывода. Уравнения движения подробно рассматриваются в курсах гидродинамики и монографиях по теплопередаче. Выделим в потоке вязкой жидкости элементарный объем с размерами ребер dx, dy и dz (рис. 4.4). Скорость в потоке изменяется только в направлении оси у, закон изменения скорости произволен.
Рис. 4.4. К выводу дифференциального уравнения движения жидкости
Согласно второму закону механики равнодействующая (a) равна произведению массы элемента на его ускорение dωx/d Рассмотрим член
Рис. 4.5. К выводу дифференциального уравнения сплошности В направлении оси Ох в параллелепипед втекает масса жидкости Условия однозначности. Полученные дифференциальные уравнения конвективного теплообмена описывают бесчисленное множество конкретных процессов. Чтобы выделить рассматриваемый процесс и определить его однозначно, к системе дифференциальных уравнений нужно присоединить условия однозначности. Условия однозначности дают математическое описание всех частных особенностей рассматриваемого явления; они состоят из: Современные методы описания процесса Конвективный теплообмен, основанные на теории пограничного слоя, позволяют получить теоретические (точные или приближённые) решения для некоторых достаточно простых ситуаций. В большинстве же встречающихся на практике случаев коэффициент теплоотдачи определяют экспериментальным путём. При этом как результаты теоретических решений, так и экспериментальные данные обрабатываются методами подобия теории куски 14) Для аналитического метода исследования конвективного теплообмена нужно решить систему дифференциальных уравнений, состоящий из: 1) Уравнения энергии (закон сохранения энергии), которое описывает температурное поле в движущейся среде. 2) Уравнения движения (импульса), которое выводят на основании второго закона Ньютона: сила равна произведению массы на ускорение 3) Уравнения неразрывности (закон сохранения массы). 4) Уравнение теплообмена (условие теплообмена на границе твердого тела и среды): α = -λ/Δt· ∂t / ∂r n=0. (10.4) Решение этих дифференциальных уравнений сложная и трудоемкая задача, и она возможна при ограниченных простых случаев. Поэтому при исследовании конвективного теплообмена применяют метод теории подобия.
Теория подобия – это наука о подобных явлениях. Подобными явлениями называются такие физические явления, которые одинаковы качественно по форме и по содержанию, т.е. имеют одну физическую природу, развиваются под действием одинаковых сил и описываются одинаковыми по форме дифференциальными уравнениями и краевыми условиями.
Обязательным условием подобия физических явлений должно быть геометрическое подобие систем, где эти явления протекают. Два физических явления будут подобны лишь в том случае, если будут подобны все величины, которые характеризуют их.
Для всех подобных систем существуют безразмерные комплексы величин, которые называются критериями подобия.
Основные положения теории подобия формулируют в виде 3-х теорем подобия. 1 теорема: Подобные явления имеют одинаковые критерии подобия. 2 теорема: Любая зависимость между переменными, характеризующая какие-либо явления, может быть представлена, в форме зависимости между критериями подобия, составленными из этих переменных, которая будет называться критериальным уравнением. 3 теорема: Два явления подобны, если они имеют подобные условия однозначности и численно одинаковые определяющие критерии подобия.
Условиями однозначности являются: наличие геометрического подобия систем; наличие одинаковых дифференциальных уравнений; существование единственного решения уравнения пр заданных граничных условиях; известны численные значения коэффициентов и физических параметров. 15. Используя теорию подобия из системы дифференциальных уравнений получить уравнение теплоотдачи (10.3) для конвективного теплообмена в случае отсутствия внутренних источников тепла в следующей критериальной форме: Nu = f2(Х; Ф; X0; Y0; Z0; Re; Gr; Pr), (10.5) где: X0; Y0; Z0 – безразмерные координаты; Nu = α ·l0/λ - критерий Нуссельта (безразмерный коэффициент теплоотдачи), характеризует теплообмен между поверхностью стенки и жидкостью (газом); Re = w·l0/ν - критерий Рейнольдса, характеризует соотношение сил инерции и вязкости и определяет характер течения жидкости (газа); Gr = (β·g·l03·Δt)/ν2 - критерий Грасгофа, характеризует подьемную силу, возникающую в жидкости (газе) вследствие разности плотностей; Pr = ν/а = (μ·cp)/λ - критерий Прандтля, характеризует физические свойства жидкости (газа); l0 – определяющий размер (длина, высота, диаметр). Процесс теплообмена между поверхностью тела и средой описывается законом Ньютона-Рихмана, которая гласит, что тепловой поток, передаваемый конвективным теплообменом прямо пропорционально разности температур поверхности тела (t'ст) и окружающей среды (t'ж): Q = α · (t'ст - t'ж)·F, (10.1) или q = α · (t'ст - t'ж), (10.2) где: α коэффициент теплоотдачи [Вт/(м2К)], характеризует интенсивность теплообмена между поверхностью тела и окружающей средой.
Факторы, которые влияют на процесс конвективного теплообмена, включают в этот коэффициент теплоотдачи. Тогда коэффициент теплоотдачи является функцией этих параметров и можно записать эту зависимость в виде следующего уравнения: α = f1(Х; Ф; lo; xc; yc; zc; wo; θ; λ; а; ср; ρ; ν; β), (10.3) где: Х – характер движения среды (свободная, вынужденная); Ф – форма поверхности; lo – характерный размер поверхности (длина, высота, диаметр и т.д.); xc; yc; zc – координаты; wo – скорость среды (жидкость, газ); θ = (t'ст - t'ж) – температурный напор; λ – коэффициент теплопроводности среды; а – коэффициент температуропроводности среды; ср –изобарная удельная теплоемкость среды; ρ –плотность среды; ν – коэффициент кинематической вязкости среды; β – температурный коэффициент объемного расширения среды. Уравнение (10.3) показывает, что коэффициент теплоотдачи величина сложная и для её определения невозможно дать общую формулу. Поэтому для определения коэффициента теплоотдачи применяют экспериментальный метод исследования. 16. Теплово́е излуче́ние — электромагнитное излучение со сплошным спектром, испускаемое нагретыми телами за счёт их внутренней энергии. Лучистый теплообмен, радиационный теплообмен, осуществляется в результате процессов превращения внутренней энергии вещества в энергию излучения, переноса энергии излучения и её поглощения веществом. Протекание процессов Л. т. определяется взаимным расположением в пространстве тел, обменивающихся теплом, свойствами среды, разделяющей эти тела. Существенное отличие Л. т. от других видов теплообмена (теплопроводности, конвективного теплообмена) заключается в том, что он может протекать и при отсутствии материальной среды, разделяющей поверхности теплообмена, так как осуществляется в результате распространения электромагнитного излучения. Лучистая энергия, падающая в процессе Л. т. на поверхность непрозрачного тела и характеризующаяся значением потока падающего излучения Qпад, частично поглощается телом, а частично отражается от его поверхности (см. рис.).
Поток поглощённого излучения Qпогл определяется соотношением: Qпогл = А Qпад, где А — поглощательная способность тела. В связи с тем, что для непрозрачного тела Qпад = Qпогл + Qoтр, где Qoтр — поток отражённого от поверхности тела излучения, эта последняя величина равна: Qoтр = (1 — А) Qпад, где 1 — А = R — отражательная способность тела. Если поглощательная способность тела равна 1, а следовательно, его отражательная способность равна 0, то есть тело поглощает всю падающую на него энергию, то оно называется абсолютно чёрным телом. Поверхность любого тела, входящего в систему Л. т., испускает потоки отражённого излучения Qoтр и собственного излучения Qcoб; суммарное количество энергии, уходящей с поверхности тела, называется потоком эффективного излучения Qэфф и определяется соотношением: Qэфф = Qoтр + Qcoб. Часть поглощённой телом энергии возвращается в систему в виде собственного излучения, поэтому результат Л. т. можно представить как разность между потоками собственного и поглощённого излучения. Величина Qpeз= Qcoб — Qпогл называется потоком результирующего излучения и показывает, какое количество энергии получает или теряет тело в единицу времени в результате Л. т. Поток результирующего излучения можно выразить также в виде Qpeз = Qэфф — Qпад, то есть как разность между суммарным расходом и суммарным приходом лучистой энергии на поверхности тела. Отсюда, учитывая, что Qпад = (Qcoб — Qpeз) / А, получим выражение, которое широко используется в расчётах Л. т.: Поглощающая способность тела —
Отражающая способность тела -
Спектральная плотность энергии - Следует отметить, что спектральная плотность энергетической светимости для абсолютно черного тела связана со спектральной плотностью энергии следующим соотношением:
Закон Стефана — Больцмана — закон излучения абсолютно чёрного тела. Определяет зависимость мощности излучения абсолютно чёрного тела от его температуры. Формулировка закона: Мощность излучения абсолютно чёрного тела прямопропорциональна площади поверхности и четвёртой степени температуры тела: P = S εσ T 4,где ε - степень черноты (для всех веществ ε < 1, для абсолютно черного тела ε = 1). При помощи закона Планка для излучения, постоянную σ можно определелить как Численное значение Закон излучения Кирхгофа — физический закон, установленный немецким физиком Кирхгофом в 1859 году. В современной формулировке закон звучит следующим образом: Отношение излучательной способности любого тела к его поглощательной способности одинаково для всех тел при данной температуре для данной частотыи не зависит от их формы, химического состава и проч. Известно, что при падении электромагнитного излучения на некоторое тело часть его отражается, часть поглощается и часть может пропускаться. Доля поглощаемого излучения на данной частоте называется поглощательной способностью тела Величины По определению, абсолютно чёрное тело поглощает всё падающее на него излучение, то есть для него
|



 на координатные оси Ох, Оу и Oz равны (4.8). Подставляя значения qx, qy и qz в уравнение (1.25), можно получить:
на координатные оси Ох, Оу и Oz равны (4.8). Подставляя значения qx, qy и qz в уравнение (1.25), можно получить:

 , х, у, z), то на основании понятия о полной производной имеем:
, х, у, z), то на основании понятия о полной производной имеем:



 , м2/с, значение которого равно отношению силы, действующей на данную частицу, к массе этой частицы. Если учитывается только сила тяжести, то
, м2/с, значение которого равно отношению силы, действующей на данную частицу, к массе этой частицы. Если учитывается только сила тяжести, то  , где
, где 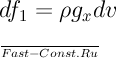
 , и на эту грань действует сила
, и на эту грань действует сила 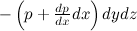 . Здесь знак минус указывает на то, что эта сила действует против направления движения жидкости. Равнодействующая сил давления равна их алгебраической сумме:
. Здесь знак минус указывает на то, что эта сила действует против направления движения жидкости. Равнодействующая сил давления равна их алгебраической сумме: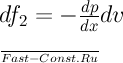



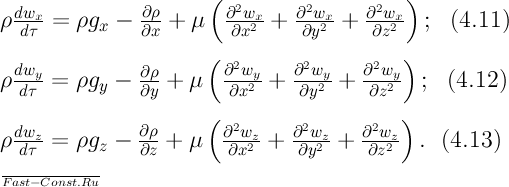




 . Его можно трактовать как сумму силы тяжести ρ0
. Его можно трактовать как сумму силы тяжести ρ0  можно написать
можно написать  , где р1=p–p0. При замене р на р1 уравнение движения будет учитывать и член ρ0
, где р1=p–p0. При замене р на р1 уравнение движения будет учитывать и член ρ0 




 и равен изменению массы данного объема во времени (∂ρ/∂
и равен изменению массы данного объема во времени (∂ρ/∂ 

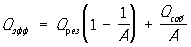 .
. — функция частоты и температуры, показывающая какая часть энергии электро-магнитного излучения, падающего на тело, поглощается телом в области частот
— функция частоты и температуры, показывающая какая часть энергии электро-магнитного излучения, падающего на тело, поглощается телом в области частот  вблизи
вблизи 
 где
где  - поток энергии, поглощающейся телом.
- поток энергии, поглощающейся телом.  - поток энергии, падающий на тело в области
- поток энергии, падающий на тело в области  - функция частоты и температуры, показывающая какая часть энергии электро-магнитного излучения, падающего на тело, отражается от него в области частот
- функция частоты и температуры, показывающая какая часть энергии электро-магнитного излучения, падающего на тело, отражается от него в области частот  где
где  - поток энергии, отражающейся от тела.
- поток энергии, отражающейся от тела.  - функция частоты и температуры, связанная с объемной плотностью излучения формулой:
- функция частоты и температуры, связанная с объемной плотностью излучения формулой: 
 - для аболютно черного тела
- для аболютно черного тела где
где  — постоянная Планка, k — постоянная Больцмана, c — скорость света.
— постоянная Планка, k — постоянная Больцмана, c — скорость света. Дж · с−1 · м−2 · К−4.
Дж · с−1 · м−2 · К−4. . С другой стороны, каждое нагретое тело излучает энергию по некоторому закону
. С другой стороны, каждое нагретое тело излучает энергию по некоторому закону  , именуемым излучательной способностью тела.
, именуемым излучательной способностью тела.
 . Поэтому функция
. Поэтому функция  совпадает с излучательной способностью абсолютно чёрного тела, описываемой законом Стефана — Больцмана, вследствие чего излучательная способность любого тела может быть найдена исходя лишь из его поглощательной способности.
совпадает с излучательной способностью абсолютно чёрного тела, описываемой законом Стефана — Больцмана, вследствие чего излучательная способность любого тела может быть найдена исходя лишь из его поглощательной способности.


