Свойства независимых событий
Теорема Если события 1) события 2) события 3) события Доказательство. 1) Поскольку события Итак, Поскольку
2) Поскольку события Итак, Поскольку 3) Если события Определение. События Определение. События Независимость в совокупности и попарная независимость событий – понятия разные. Пример. Три грани треугольной пирамиды окрашены соответственно в белый, зеленый, желтый цвета. На последней грани присутствуют все три цвета. Случайным образом выбирают грань. Найти вероятности событий: Решение. Желтый цвет имеется на двух гранях из четырех, т.о. Т.е. все события попарно независимы. Однако события не являются независимыми в совокупности:
Теорема. (О появлении хотя бы одного из независимых событий) Пусть вероятность появления каждого из п событий Доказательство. Поскольку по закону Де Моргана то
Пример. Из полной колоды карт (52 шт.) одновременно вынимают четыре карты. Найти вероятность того, что среди этих четырех карт будет хотя бы одна бубновая карта. Решение. Пусть событие Пример. Вероятность хотя бы одного попадания в мишень стрелком при трех выстрелах равна 0,875. Найти вероятность попадания в мишень при одном выстреле.
Если обозначить р – вероятность попадания стрелком в мишень при одном выстреле, то вероятность промаха при одном выстреле, очевидно, равна (1 – р). Вероятность трех промахов из трех выстрелов равна (1 – р)3. Эта вероятность равна 1 – 0,875 = 0,125, т.е. в цель не попадают ни одного раза. Получаем: Пример. Чему равна вероятность того, что при бросании трех игральных костей 6 очков появится хотя бы на одной из костей?
|

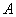 и
и  независимы, то:
независимы, то: независимы;
независимы; и
и 
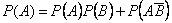 .
.
 .
. , то
, то  , что свидетельствует о независимости событий
, что свидетельствует о независимости событий 
 .
.
 .
. , то
, то 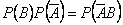 , что свидетельствует о независимости событий
, что свидетельствует о независимости событий  независимы в совокупности, если
независимы в совокупности, если .
.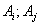 события
события  и
и  независимы.
независимы. =«на грани есть зеленый цвет»;
=«на грани есть зеленый цвет»;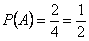 ; аналогично:
; аналогично: 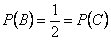 . Вероятность того, что на выпавшей грани есть два цвета -
. Вероятность того, что на выпавшей грани есть два цвета - 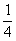 , т.е.
, т.е.  . Таким образом,
. Таким образом,

 ,
,
 . Вероятность появления хотя бы одного события, равна
. Вероятность появления хотя бы одного события, равна ,
, 
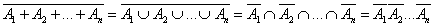 ,
, .
. . Событие
. Событие  , тогда
, тогда  ,
, 




