Решение. Вероятность выпадения 6 очков при одном броске кости (событие ) равна
Вероятность выпадения 6 очков при одном броске кости (событие
Тогда вероятность того, что хотя бы один раз выпадет 6 очков, равна
Пример. Один из трех стрелков производит два выстрела. Вероятность попадания в цель при одном выстреле для первого стрелка равна 0,4, для второго – 0,6, для третьего – 0,8. Найти вероятность того, что в цель попадут два раза. Вероятность того, что выстрелы производит первый, второй или третий стрелок равна Вероятности того, что один из стрелков, производящих выстрелы, два раза попадает в цель, равны:
- для первого стрелка: - для второго стрелка: - для третьего стрелка:
Искомая вероятность равна:
Решение. Обозначим попадание в цель первым стрелком – событие А, вторым – событие В, промах первого стрелка – событие
Вероятность того, что первый стрелок попадет в мишень, а второй – нет равна Вероятность того, что второй стрелок попадет в цель, а первый – нет равна Тогда вероятность попадания в цель только одним стрелком равна Тот же результат можно получить другим способом – находим вероятности того, что оба стрелка попали в цель и оба промахнулись. Эти вероятности соответственно равны: Тогда вероятность того, что в цель попадет только один стрелок равна:
Пример. Вероятности того, что нужная деталь находится в первом, втором, третьем или четвертом ящике, соответственно равны 0,6, 0,7, 0,8, 0,9. Найти вероятности того, что эта деталь находится: а) не более, чем в трех ящиках; б) не менее, чем в двух ящиках.
|

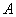 ) равна
) равна  . Вероятность того, что не выпадет 6 очков (событие
. Вероятность того, что не выпадет 6 очков (событие  ) -
) -  . Вероятность того, что при броске трех костей не выпадет ни разу 6 очков равна
. Вероятность того, что при броске трех костей не выпадет ни разу 6 очков равна  .
.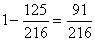 .
. .
.
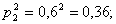
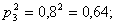

 , промах второго – событие
, промах второго – событие  .
.








