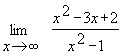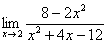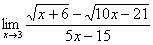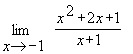- Подставить в выражение предельное значение аргумента.
- Определить есть или нет неопределенность. Если нет, дать ответ.
- Если неопределенность есть, то по ее виду выбрать одно из правил устранения этой неопределенности.
- Преобразовать выражение согласно выбранному правилу, и к новой форме предела применить данный алгоритм, начиная с п.1.
Правило 1.
Чтобы раскрыть неопределенность вида 0/0,заданную отношением двух многочленов, необходимо предварительно выделить критический множитель(т.е. множитель, равный нулю при предельном значении х), сократить на него, а затем перейти к пределу
 В числителе и знаменателе вынести x в максимальной степени, если это возможно. Заметим, что
В числителе и знаменателе вынести x в максимальной степени, если это возможно. Заметим, что  , а
, а  , где c - любое число.
, где c - любое число.
Правило 2.
 Числитель и знаменатель разделить одновременно на
Числитель и знаменатель разделить одновременно на  , если это возможно. Необходимо иметь в виду, что
, если это возможно. Необходимо иметь в виду, что  , а
, а  , где c - число, отличное от нуля.
, где c - число, отличное от нуля.
Правило 3.
При вычислении пределов от иррациональных выражений, не попадающих в предыдущие правила, следует избавиться от корней, входящих в неопределенность. Возможны следующие способы:
3.1. замена переменной  , позволяющая извлечь корни, входящие в неопределенность;
, позволяющая извлечь корни, входящие в неопределенность;
3.2. дополнение до формулы, позволяющей возвести корень в соответствующую ему степень; здесь используются формулы: 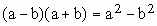 ;
;  .
.


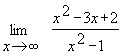
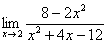
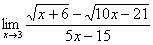

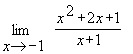
Пример 4.

 В числителе и знаменателе вынести x в максимальной степени, если это возможно. Заметим, что
В числителе и знаменателе вынести x в максимальной степени, если это возможно. Заметим, что  , а
, а  , где c - любое число.
, где c - любое число. Числитель и знаменатель разделить одновременно на
Числитель и знаменатель разделить одновременно на  , если это возможно. Необходимо иметь в виду, что
, если это возможно. Необходимо иметь в виду, что  , а
, а  , где c - число, отличное от нуля.
, где c - число, отличное от нуля. , позволяющая извлечь корни, входящие в неопределенность;
, позволяющая извлечь корни, входящие в неопределенность;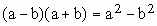 ;
;  .
.