РАЗЛИЧНЫХ ЧАСТОТ
ИССЛЕДОВАНИЕ СЛОЖЕНИЯ
Цель работы: исследование траектории движения точки, участвующей в двух взаимно перпендикулярных колебаниях; проверка градуировки шкалы генератора электрических синусоидальных сигналов Г3-120, используя метод фигур Лиссажу.
Если материальная точка одновременно участвует в двух колебательных процессах, происходящих во взаимно перпендикулярных направлениях, и частоты этих колебаний кратны друг другу, то результирующее движение материальной точки происходит по криволинейной траектории, называемой фигурой Лиссажу. Форма фигур Лиссажу зависит от частот, разности фаз и амплитуд слагаемых колебаний. Рассмотрим результат сложения двух таких гармонических колебаний одинаковой циклической частоты w, происходящих во взаимно перпендикулярных направлениях вдоль координатных осей X и У. Для простоты начало отсчета выберем так, чтобы фаза первого колебания была равна нулю
где j — разность фаз обоих колебаний, А и В — их амплитуды. Уравнение траектории результирующего колебания находится исключением из выражений (1) параметра t. Записываем уравнения складываемых колебаний в виде
и, заменяя во втором уравнении
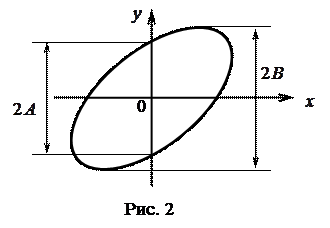
Ориентация осей эллипса и его размеры зависят от амплитуд А и В складываемых колебаний и разности фаз j. Рассмотрим некоторые частные случаи, представляющие физический интерес. 1. Пусть j = mp (m= 0, ±1, ±2, ±3 …). В этом случае эллипс вырождается в отрезок прямой у = ± где знак “+” соответствует нулю и четным значениям m (рис.1,а), а знак “–” — нечетным значениям m (рис.1,б).
Если частоты взаимно перпендикулярных колебаний различны, то замкнутая траектория довольно сложна. Форма фигур Лиссажу зависит от соотношения амплитуд, частот и разности фаз складываемых колебаний. По виду таких фигур Лиссажу оказывается возможным определить частоту одного из колебаний, если частота другого известна. В настоящей работе такой способ определения частот осуществляется с помощью осциллографа. На вертикально отклоняющие пластины подается напряжение с известной частотой wу, на горизонтально отклоняющие пластины ‑ исследуемое напряжение с частотой wх. На полученной фигуре Лиссажу проводят две произвольные взаимно перпендикулярные прямые
В данном случае Определяют неизвестную частоту колебаний по формуле вывод которой мы не приводим. Для примера, иллюстрируемого на рис.3,
|



 , (1)
, (1)

 на x / A и sin wt на
на x / A и sin wt на  , после несложных преобразований (осуществите их самостоятельно) получим уравнение эллипса
, после несложных преобразований (осуществите их самостоятельно) получим уравнение эллипса . (2)
. (2) (3)
(3)
 и
и  параллельные осям X и Y, как показано на рис.3. Определяют число
параллельные осям X и Y, как показано на рис.3. Определяют число  точек пересечения фигуры с прямой
точек пересечения фигуры с прямой  пересечений с прямой
пересечений с прямой 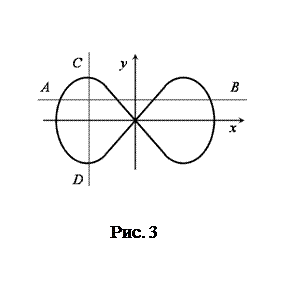
 и
и  .
. ,
, .
.


