Вопрос 1. Затухание колебаний в системах с вязким трением.
1. Амплитуда затухающих колебаний маятника за время t1 = 5 мин уменьшилась в n1 = 2 раза. За какое время t2 амплитуда уменьшится в n2 = 8 раз? 2. За время t = 8 мин амплитуда затухающих колебаний уменьшилась в 3 раза. Определите коэффициент затухания d. Какова добротность этой колебательной системы, если период колебаний Т = 10 с. Сколько полных колебаний совершит система до полной остановки? 3. Логарифмический декремент затухания маятника равен q = 3×10-3. Определите число полных колебаний, которое должен совершить маятник, чтобы амплитуда его колебаний уменьшилась в 2 раза. 4. Определите период Т затухающих колебаний системы, если период собственных колебаний Т = 1 с, а логарифмический декремент затухания равен q = 0, 628. 5. Определите добротность маятника, если за время, в течение которого было совершено 10колебаний, амплитуда уменьшилась в 2 раза. Сколько колебаний совершит маятник до остановки? За какое время это произойдет? 6. Энергия затухающих колебаний маятника за время t = 100 с уменьшилась в 100 раз. Определите коэффициент сопротивления среды r, если масса маятника 100 г. Вопрос 1. Затухание колебаний в системах с вязким трением. Рассмотрим колебательную систему, в которой действует сила вязкого трения. Примером такой колебательной системы может служить математический маятник, совершающий колебания в воздушной среде.
В этом случае при выведении системы из положения равновесия на маятник будут действовать две силы: квазиупругая сила и сила сопротивления (сила вязкого трения). Второй закон Ньютона запишется следующим образом:
Знак «-» указывает на то, что сила вязкого трения всегда направлена против скорости движения тела.
Тогда выражение (1) в проекции на ось ОХ, вдоль которой происходят колебания, будет выглядеть следующим образом:
Учтем, что проекция скорости есть первая производная от координаты тела, а проекция ускорения – вторая производная от координаты:
Тогда уравнение (2) примет вид:
Разделив все члены уравнения на m и обозначив
получим уравнение движения в следующем виде: d - коэффициент затухания, он зависит от коэффициента трения r, w0 - циклическая частота идеальных колебаний (в отсутствие трения).
Учтем, что
Окончательно получаем
Обратите внимание на математическую тождественность дифференциальных уравнений (3) и (3’). В этом нет ничего удивительного. Мы уже показывали абсолютную математическую тождественность процесса колебания маятника и электромагнитных колебаний в контуре. Очевидно, процессы затухания колебаний в контуре и в системах с вязким трением происходят тоже одинаково.
Решив уравнение (3), мы получим ответы на все поставленные выше вопросы.
Уравнение (3) можно привести к уравнению гармонических колебаний, применив подстановку
Тогда уравнение (3) примет вид
Если d2 < w02, то величина w02 - d2 > 0, ее можно обозначить w2 = w02 - d2. Получаем знакомое уравнение гармонических колебаний. Решение этого уравнения нам известно
Тогда для искомого уравнения (3) получаем окончательный результат
Нетрудно видеть, что заряд конденсатора в реальном колебательном контуре будет изменяться по закону
Анализ полученного результата:
1. В результате совместного действия квазиупругой силы и силы сопротивления система может совершать колебательное движение. Для этого должно выполняться условие w02 - d2 > 0. Иными словами, трение в системе должно быть невелико. 2. Частота затухающих колебаний w не совпадает с частотой колебаний системы в отсутствие трения w2 = w02 - d2 < w02. С течение времени частота затухающих колебаний остается неизменной. 3. Если коэффициент затухания d мал, то частота затухающих колебаний близка к собственной частоте w0. При d2 ® w02 частота уменьшается, а период возрастает до бесконечности. При d2 >w02 колебаний не возникает: система, выведенная из положения равновесия, медленно (апериодически) возвращается в положение равновесия. 4.
Амплитуда затухающих колебаний, как это и было предсказано ранее, уменьшается с течением времени. Это убывание амплитуды происходит по экспоненциальному закону.
5. Если w02 - d2 < 0, то есть трение в системе велико, то уравнение (3) имеет решение вида
где
Вопрос 2. Как быстро затухают колебания в системах с вязким трением?
|


 Мы знаем, что при малых скоростях сила вязкого трения пропорциональна скорости движения:
Мы знаем, что при малых скоростях сила вязкого трения пропорциональна скорости движения:




 Прежде чем решать уравнение (3), рассмотрим колебательный контур. Активное сопротивление катушки
Прежде чем решать уравнение (3), рассмотрим колебательный контур. Активное сопротивление катушки  включено последовательно с емкостью С и индуктивностью L.
включено последовательно с емкостью С и индуктивностью L. Запишем второй закон Кирхгофа
Запишем второй закон Кирхгофа ,
,  ,
,  .
. Тогда второй закон Кирхгофа примет вид:
Тогда второй закон Кирхгофа примет вид: Разделим обе части уравнения на
Разделим обе части уравнения на  :
: Введем обозначения
Введем обозначения





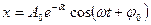




 . Непосредственной подстановкой легко убедиться, что функция (4) действительно является решением уравнения (3). Очевидно, что сумма двух экспоненциальных функций не является периодической функцией. С физической точки зрения это означает, что колебания в системе не возникнут. После выведения системы из положения равновесия она будет медленно в него возвращаться. Такой процесс называется апериодическим.
. Непосредственной подстановкой легко убедиться, что функция (4) действительно является решением уравнения (3). Очевидно, что сумма двух экспоненциальных функций не является периодической функцией. С физической точки зрения это означает, что колебания в системе не возникнут. После выведения системы из положения равновесия она будет медленно в него возвращаться. Такой процесс называется апериодическим.
 или
или


