Расчет прочности на действие поперечной силы по наклонному сечению
Прочность наклонных сечений на действие поперечной силы у опоры B при Аsw = 151 мм2 (3 8А400) с шагом s = 150 мм в соответствии с требованиями п. 5.21 и 3.35 [3]:
(см. формулу (3.48) [3]). Так как qsw = 383,58 кН/м > 0,25 Rbtb = 0,25 · 0,81 · 1337 · 0,3 = = 81,22 кН/м, Mb = 1,5 Rbtbh 02 = 1,5 · 0,81 · 1337 · 0,3 · 0,692 = 173,5 кН·м (см. формулу (3.46) [3]). Определяем длину проекции невыгоднейшего наклонного сечения c. При расчете элемента на действие равномерно распределенной нагрузки q значение c принимают равным Так как c = Принимаем c = 0,73 м. Длину проекции наклонной трещины c 0 принимают равной c, но не более 2 h 0 = 0,69 · 2 = 1,38м (см. п. 3.31 [3]). Принимаем длину проекции наклонной трещины c 0 = c = 0,0,73 м. Тогда Qsw = 0,75 qswc 0 = 0,75 * 286,8 * 0,83 = кН. Поперечную силу, воспринимаемую бетоном, определяют по формуле Q = Mb/с, но не более Qb ,max = 2,5 Rbtbh 0 и не менее Qb, min = 0,5 Rbtbh 0 (см. п. 3.31 [3]). Qb, min = 0,5 Rbtbh 0 = 0,5 · 0,81 · 103 · 0,17 · 0,415 = 28,57кН < Qb =42,86< < Qb ,max = 2,5 Rbtbh 0 = 2,5 · 0,81 · 103 · 0,17 · 0,415 = 142,86 кН. Принимаем Qb = 42,86 кН. Расчет изгибаемых элементов по наклонному сечению производят из условия Q ≤ Qb +Qsw, где Q – поперечная сила в наклонном сечении с длиной проекции c; при вертикальной нагрузке, приложенной к верхней грани элемента, значение Q принимается в нормальном сечении, проходящем на расстоянии c от опоры; при этом следует учитывать возможность отсутствия временной нагрузки на приопорном участке длиной c. Q = Q- gc = 71,44 – 18,65 · 0,83 = 53,95 кН. При Qsw + Qb = 40,21 + 42,86 = 83,07 кН > Q = 53,95 м, т. е. прочность наклонных сечений у опоры B и C обеспечена. В средней части пролета Q 1 = Определяем поперечную силу, воспринимаемую бетоном. Mb = 1,5 Rbtbh 02 = 1,5 · 0,81 · 1000 · 0,3 · 0,692 = 173,5 кН·м (см. формулу (3.46) [3]). Длина проекции невыгоднейшего наклонного сечения с= Принимаем c = 1,26 м. Поперечную силу, воспринимаемую бетоном, определяем по формуле (3.46) [3], Qb, min = 0,5 Rbtbh 0 (см. п. 3.31 [3]). Qb, min = 0,5 Rbtbh 0 = 0,5 · 0,81 · 103 · 0,3 · 0,69 = 83,8 кН < 137, < Qb, max = 2,5 Rbtbh 0 = 2,5 · 0,81 · 103 × 0,3 · 0,69 = 419 кН. Принимаем Qb = 137,7 кН < Q 1 = 177,3 кН, т. е. поперечная сила не может быть воспринята только бетоном. Поэтому предусматриваем ус- тановку поперечной арматуры с шагом не более: s Кроме того, в соответствии с п. 3.35 [2] шаг хомутов, учитываемых в расчете
Шаг поперечных стержней принимаем s= 300 мм.
(см. формулу (3.48) [3]). Так как qsw = 143,5 кН/м > 0,25 Rbtb = 0,25 · 0,81 · 1000 · 0,3 = = 60,75 кН/м, хомуты учитываются в расчете и Mb = 1,5 Rbtbh 02 = = 1,5 · 0,81 · 1000 · 0,3 · 0,692 = 173,5 кН·м (см. формулу (3.46) [3]). Определяем c. Так как с= c = Принимаем c = 0,89м. Длину проекции наклонной трещины c 0 принимают равной c, но не более 2 h 0 = 0,69 · 2 = 1,38м (см. п. 3.31 [3]). Принимаем c 0 = c = 0,89 м. Тогда Qsw = 0,75 qswc 0 = 0,75 * 286,8 * 0,83 = кН. Поперечную силу, воспринимаемую бетоном, опеделяют по формуле Принимаем Qb = 194,9 кН. При Qsw + Qb = 95,8 + 194,9 = 290,7 кН > Q 1 = 177,3 кН прочность наклонных сечений в средней части пролетов между опорами обеспече- на при поперечных стержнях 8 мм класса А400 с шагом s= 300 мм. Расчет прочности на действие момента по наклонному сечению На средних опорах В и С концы стержней неразрезного ригеля при- варены к надежно заанкеренным закладным деталям, поэтому расчет прочности наклонных сечений на действие момента не производим (см. п. 3.44 [3]). Расчет колонны (для специальностей ВВ и СД) Принимаем к расчету наиболее нагруженную колонну среднего ряда. Расчет прочности колонны производим в наиболее нагруженном сечении – у обреза фундамента. Нагрузку на колонну с учетом ее веса определяем от опирающихся на нее ригелей трех вышележащих междуэтажных перекрытий (нагрузка от кровли передается на наружные кирпичные стены). В качестве расчетной схемы колонны условно принимаем сжатую со случайным эксцентриситетом стойку, защемленную в уровне обреза фундамента и шарнирно закрепленную в уровне середины высоты ригеля (рис. 30). Рисунок 30
Расчетная длина колонны нижнего этажа с шарнирным опиранием на одном конце, а на другом конце с податливой заделкой 0,9l (см. п. 3.55 [2]). l0 = 0,9l = 0,9(hэт +0,7 - hп - hp)= 0,9(4,2+0,7 - 0,45- 0,75)= 3,33 м, где hэт – высота этажа по заданию; 0,7 м – расстояние от обреза фундамента до уровня чистого пола; hп – высота панели перекрытия; hр – высота сечения ригеля. Принимаем колонну сечением 40 40 см, а = а = 4 см. Расчетная нагрузка на колонну в уровне обреза фундамента N = (g +v) ln+Gc = (26,7+88,4)* 6,48*3+58,520= 2288,9 кН, где g + v – постоянная и временная нагрузка на 1 пог. м ригеля (см. сбор нагрузки на неразрезной ригель); l = lср – расстояние между осями колонн, на которые опирается средний ригель (если разрезной ригель имеет три пролета l = (lкр +lср)/ 2); n = 3 – число перекрытий; Gc – вес колонны. Gc = Кратковременно действующая часть расчетной нагрузки Nsh = vsh nAгрn где по заданию vsh n = 1,5 кН/м2; A= lпlp = 6,14 *6,48= 39,8 м2 – грузовая площадь перекрытия, с которой нагрузка передается на среднюю колонну; Длительно действующая часть расчетной нагрузки
С учетом коэффициента надежности по ответственности n = 0,95 (см. прил. 7* [18]). N = 2288,9 0,95= 2174,5 кН; N = 2073,9 0,95 =1970,2 кН. Случайный эксцентриситет в приложении сжимающей нагрузки согласно п. 3.49 [3] ea ≥hc /30= 400 / 30=13,3 мм; ea ≥ l0 / 600= 3330/ 600= 5,55 мм; ea ≥10 мм. Принимаем e0 = ea =13,3 мм. Бетон класса В25 с Rb = 0,9 · 14,5 = 13,05 МПа, Rbt = 0,9 · 1,05 = 0,95 МПа (см. табл. 2.2 [2]), где b1 = 0,9; Еb = 30 · 103 МПа (см. табл. 2.4 [3]). Продольная арматура класса А400 с Rs = Rsc = 355 МПа (см. табл. 2.6 [3]); Еs = 20 · 104 МПа (см. п. 2.20 [3]). Расчет сжатых элементов из бетонов классов В15–В35 на действие продольной силы, приложенной со случайным эксцентриситетом, при l0 = 2,85 м < 20 · hc = 20 · 0,4 = 8 м допускается производить из условия (см. п. 3.58 [3]) N ≤ где
где Задаемся
Проектируем колонну квадратного сечения h= b= Принимаем размеры поперечного сечения колонны кратными 0,05 м. Тогда h = b = 0,4 м, А = h · b = 0,4 · 0,4 = 0,16 м2. Задаемся
Коэффициент армирования
незначительно отличается (не более 0,005) от = 0,01, которым задавались. По сортаменту принимаем 4Ø 18A400 с Аs,tot = 1018 мм2. Поперечные стержни в сварных каркасах назначаем диаметром 6 мм из арматуры класса А240 в соответствии с п. 5.23 [3] с шагом s = 250 мм (s ≤15 *d =15 *18= 270 мм и не более 500 мм.
|

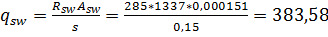 кН/м
кН/м , а если при этом
, а если при этом  или
или  , следует принимать
, следует принимать  (см. п. 3.32 [3]).
(см. п. 3.32 [3]). =1.6 м
=1.6 м  , то
, то =0,73 м, но не более 3 h 0 = 3 · 0,415 = 1,245 м (см. п. 3.32 [3]).
=0,73 м, но не более 3 h 0 = 3 · 0,415 = 1,245 м (см. п. 3.32 [3]). кН
кН , но не более Qb, max = 2,5 Rbtbh 0 и не менее
, но не более Qb, max = 2,5 Rbtbh 0 и не менее 0,5 h 0 = 0,5 · 690 = 345 мм; s
0,5 h 0 = 0,5 · 690 = 345 мм; s 
 м, то
м, то ,но не более Qb, max = 2,5 Rbtbh 0 и не менее Qb, min = 0,5 Rbtbh 0 = 0,5 · 0,81 · 103 · 0,3 · 0,69 = 83,8
,но не более Qb, max = 2,5 Rbtbh 0 и не менее Qb, min = 0,5 Rbtbh 0 = 0,5 · 0,81 · 103 · 0,3 · 0,69 = 83,8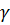 bc
bc  (hэтn+0,7)= 25 *0,4* 0,4 *1,1(4,2 *3+0,7)= 58,52 кН.
(hэтn+0,7)= 25 *0,4* 0,4 *1,1(4,2 *3+0,7)= 58,52 кН. = N -Nsh = 2288,9 - 215= 2073,9 кН;
= N -Nsh = 2288,9 - 215= 2073,9 кН; (RbA+Rsc As,tot ),
(RbA+Rsc As,tot ), ,
,  ,
, = 0,01. Тогда
= 0,01. Тогда м2.
м2. =
=  = 0,382 м.
= 0,382 м. =0,01. Тогда
=0,01. Тогда ;
; 

 = 0,9 (см. табл. 3.5 [3]);
= 0,9 (см. табл. 3.5 [3]);  = 0,9087 (см. табл. 3.6 [3]);
= 0,9087 (см. табл. 3.6 [3]); = 0,9 + 2(0,9087– 0,9)0,272 = 0,905 <
= 0,9 + 2(0,9087– 0,9)0,272 = 0,905 <  =902*10-6=902мм2.
=902*10-6=902мм2.



