Расчет прочности на действие поперечной силы по наклонному сечению.
Расчет прочности по наклонной полосе между наклонными сечениями производим из условия 3.43[2]
(см. формулу (3.48) [3]). Так как qsw = 64,6 кН/м > 0,25 Rbtb = 0,25 · 0,81 · 1337 · 0,17 = = 46,03 кН/м, Mb = 1,5 Rbtbh 02=1,5*0,81*1337*0,17*0,4152=47,56 кН·м (см. п. 3.31 и формулу (3.46) [3]). Определяем длину проекции невыгоднейшего наклонного сечения c. При расчете элемента на действие равномерно распределенной нагрузки q значение c принимают равным Отсюда Так как c = Принимаем c = 1,24 м. Длину проекции наклонной трещины c 0 принимают равной c, но не более 2 h 0 = 0,415 · 2 = 0,83 м (см. п. 3.31 [3]). Принимаем длину проекции наклонной трещины c 0 = c = 0,83 м. Тогда Qsw = 0,75 qswc 0 = 0,75 * 64,6 * 0,83 = 40,21 кН. Поперечную силу, воспринимаемую бетоном, определяют по формуле Q = Mb/с, но не более Qb ,max = 2,5 Rbtbh 0 и не менее Qb, min = 0,5 Rbtbh 0 (см. п. 3.31 [3]). Qb, min = 0,5 Rbtbh 0 = 0,5 · 0,81 · 103 · 0,17 · 0,415 = 28,57кН < Qb =42,86< < Qb ,max = 2,5 Rbtbh 0 = 2,5 · 0,81 · 103 · 0,17 · 0,415 = 142,86 кН. Принимаем Qb = 42,86 кН. Расчет изгибаемых элементов по наклонному сечению производят из условия Q ≤ Qb +Qsw, где Q – поперечная сила в наклонном сечении с длиной проекции c; при вертикальной нагрузке, приложенной к верхней грани элемента, значение Q принимается в нормальном сечении, проходящем на расстоянии c от опоры; при этом следует учитывать возможность отсутствия временной нагрузки на приопорном участке длиной c. Q = Q- vc = 71,44 – 18,65 · 0,83 = 53,95 кН. При Qsw + Qb = 40,21 + 42,86 = 83,07 кН > Q = 53,95 кН, прочность наклонных сечений обеспечена (см. п. 3.31 [3]). Поскольку продольная растянутая арматура ребер по концам приварена к закладным деталям, проверку наклонных сечений на действие момента не производим. Расчет разрезного ригеля (для специальностей ВВ и СД) Согласно разбивочной схеме ригель представляет собой разрезную многопролетную конструкцию со свободным опиранием концов на кирпичные стены здания. В курсовом проекте рассчитываем средний пролет ригеля. За расчетный пролет разрезного ригеля принимается расстояние между центрами площадок опирания ригеля на консоли колонн (см. рис. 18): l0 = lср - a / 2 -a / 2- hк= 6,685 – 0,125 – 0,125 – 0,4 = 6,008 м. Нагрузка от сборных панелей передается продольными ребрами в виде сосредоточенных сил. Для упрощения расчета без большой погрешности при четырех и более сосредоточенных силах разрешается заменять такую нагрузку эквивалентной (по прогибу), равномерно распределенной по длине ригеля. Расчетная схема ригеля представлена на рис. 26.
Рисунок 26 По рекомендациям [12] принимаем ригель сечением 30×70 см. Нагрузки на ригель, кН/м
*Определение нагрузки от веса пола и панелей см. «Сбор нагрузки на продольные ребра плиты»: g п n = 3,97 кН/м – нормативная постоянная нагрузка на 1 пог. м двух продольных ребер плиты; g п = 4,419 кН/м – расчетная постоянная нагрузка на 1 пог. м двух продольных ребер плиты; l н = 6,14 м – номинальная длина панелей; b н = 1,295 м – номинальная ширина панелей. Полная нагрузка на ригель: нормативная gn + vn = 24,07 + 73,68 = 97,75 кН/м; расчетная g + v = 26,73 + 88,42 = 115,15 кН/м. Кратковременно действующая часть нагрузки на ригель: нормативная vsh n = 1,5 · 6,14 = 9,21 кН/м; расчетная vsh = vsh n Длительно действующая часть расчетной нагрузки на ригель: gl +vl = g +v - vsh =115,15 – 11,05 = 104,1 кН/м. (gl +vl)/(g+v)=104,1/115,15= 0,904 >0,9, поэтому
|


 ,а если при этом
,а если при этом  или
или  , следует принимать
, следует принимать  (см. п. 3.32 [3]).
(см. п. 3.32 [3]). =
= 
 =1.6 м
=1.6 м  , то
, то

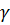 f = 9,21 · 1,2 = 11,05 кН/м, где по заданию vsh n =1,5 кН/м2.
f = 9,21 · 1,2 = 11,05 кН/м, где по заданию vsh n =1,5 кН/м2.


