ПАСПОРТ
V1: Понятия, принципы и средства исследования операций.
I: S: Моделирование – это… -: процесс построения моделей -: процесс изучения моделей +: процесс построения, изучения и применения моделей -: конструирование моделей
I: S: Моделирование в экономике – это… +: воспроизведение экономических объектов и процессов в ограниченных, малых, экспериментальных формах, в искусственно созданных условиях -: построение и изучение моделей реально существующих объектов, процессов или явлений с целью получения объяснений этих явлений -: воспроизведение экономических объектов и процессов в ограниченных, малых, экспериментальных формах, в реальных условиях
I: S: Выберите правильное определение модели: +: материально или мысленно представляемый объект, который в процессе исследования замещает объект – оригинал; при этом отражает его наиболее существенные свойства -: исследование объектов познания не непосредственно, а косвенным путем, при помощи анализа других вспомогательных объектов -: способ достижения цели, определенным образом упорядоченная деятельность -: метод научного познания реально существующих объектов
I: S: Выберите правильное определение моделирования: +: исследование объектов познания не непосредственно, а косвенным путем, при помощи анализа других вспомогательных объектов -: материально или мысленно представляемый объект, который в процессе исследования замещает объект – оригинал; при этом отражает его наиболее существенные свойства -: способ достижения цели, определенным образом упорядоченная деятельность -: идеальный образ реально существующего объекта, который в процессе исследования замещает объект – оригинал; при этом отражает его наиболее существенные свойства
I: S: В зависимости от учета фактора времени выделяют модели: +: статические и динамические -: стохастические и детерминированные -: статистические и динамические -: стохастические и динамические
I: S: Все множество моделей может быть разделено на два класса: +: материальные и идеальные -: знаковые и интуитивные -: знаковые и идеальные -: модели геометрического подобия и знаковые модели
I: S: К классу идеальных моделей относятся: +: знаковые и интуитивные -: знаковые модели и модели – аналоги -: модели геометрического подобия и модели – аналоги -: интуитивные модели и модели – аналоги
I: S: Результаты на выходе однозначно определяются управляющими воздействиями без учета случайных факторов в моделях: +: детерминированных -: имитационных -: стохастических
I: S: Описывают свойства объекта по состоянию к определенному моменту времени модели: +: статические -: динамические -: трендовые
I: S: Описывают экономическую систему в развитии модели: +: динамические -: статические -: оптимизационные
I: S: Модели, предназначенные для выбора наилучшего варианта из определенного числа вариантов производства: +: оптимизационные -: балансовые -: имитационные -: экономико-статистические
I: S: Модели, которые выражают требование соответствия наличия ресурсов и их использования: +: балансовые -: оптимизационные -: имитационные -: экономико-статистические
I: S: Создатель первой в мире модели народного хозяйства: +: Ф. Кенэ. -: У. Петти -: К. Маркс
I: S: В сфере принятия экономических решений критерий оптимальности – это показатель,… -: выражающий меру экономического эффекта принимаемого управленческого решения +: выражающий предельную меру экономического эффекта принимаемого управленческого решения для сравнительной оценки возможных решений и выбора наилучшего из них -: выражающий качество функционирования оргсистемы
I: S: Критерий оптимальности носит… -: качественный характер +: количественный характер -: переменный характер
I: S: В роли критерия оптимальности могут выступать… +: максимум прибыли +: минимум затрат -: прибыль -: издержки
I: S: Компромиссное решение – это решение, …. -: единственно верное решение +: оптимальное по всем критериям -: приемлемое решение
I: S: Основной задачей экономики является… +: рациональное ведение хозяйства -: эффективная деятельность предприятий -: разумное использование ресурсов
I: S: Задачу математической оптимизации можно сформулировать как +: определение таких значений некоторых переменных величин, удовлетворяющих ряду ограничений, при которых достигается максимум определенной функции -: определение значений некоторых переменных величин, удовлетворяющих ряду ограничений -: определение таких значений некоторых переменных, при которых достигается максимум определенной функции
I: S: Математически задача рационального ведения хозяйства является задачей… -: отбора из возможных вариантов таких значений инструментальных величин, при которых целевая функция не достигает максимума -: отбора из множества возможных вариантов таких значений инструментальных величин, при которых целевая функция достигает нулевого значения +: отбора из множества возможных вариантов таких значений инструментальных величин, при которых целевая функция достигает максимума
I: S: Статистическая задача рационального ведения хозяйства (рациональной деятельности) связана с… +: распределением ограниченных ресурсов на различные цели в определенный момент времени -: нахождением оптимального решения -: целевой функцией, позволяющей найти оптимальное решение
I: S: Статистическая задача рационального ведения хозяйства в математической форме состоит в нахождении значений переменных, максимизирующих заданную функцию и удовлетворяющих системе ограничений и называется… +: задачей математического программирования -: задачей линейного программирования -: задачей нелинейного программирования -: задачей динамического программирования
I: S: Оптимизационная модель состоит из: -: целевой функции; системы ограничений, определяющими эту область -: уравнений и неравенств -: уравнений, тождеств и неравенств +: целевой функции; области допустимых решений; системы ограничений, определяющими эту область
I: S: Область допустимых решений – это область, в пределах которой осуществляется: -: выбор целевой функции +: выбор решений -: решение системы уравнений -: решение системы неравенств
I: S: Оптимизационные задачи решаются методами: -: линейного программирования -: динамического программирования +: математического программирования -: целочисленного программирования
I: S: Целевая функция – это… -: краткое математическое изложение решения данной задачи +: краткое математическое изложение цели данной задачи -: подробное математическое изложение цели данной задачи
I: S: В оптимизационных задачах на min обычно коэффициенты при искусственных переменных: +: в 1000 раз должны быть больше, чем значения коэффициентов при основных переменных -: в 100 раз должны быть больше, чем значения коэффициентов при основных переменных -: в 1000 раз должны быть меньше, чем значения коэффициентов при основных переменных -: в 10 раз должны быть меньше, чем значения коэффициентов при основных переменных
I: S: В оптимальном решении задачи все искусственные переменные должны быть: +: равными нулю -: больше нуля -: не равными нулю
I: S: В оптимизационных задачахна мах искусственные переменные в целевой функции задачи должны иметь: -: небольшие отрицательные коэффициенты (-М) +-: большие отрицательные коэффициенты (-М) -: большие положительные коэффициенты (+М) -: небольшие положительные коэффициенты (+М)
I: S: Какое из следующих утверждений истинно? В методах прямого поиска при поиске экстремума целевой функции А) используются значения целевой функции и ее производной В) используются только значения целевой функции -: A – нет, B - нет -: A – да, B – да -: A – да, B – нет +: А – нет, В – да
I: S: Какое из следующих утверждений истинно? Выпуклая область обладает следующим свойством А) вместе с любыми двумя своими точками содержит и соединяющий их отрезок В) является связной +: А – да, В – да -: A – нет, B - нет -: A – да, B – нет -: A – нет, B – да
I: S: Какое из следующих утверждений истинно? Задача математического программирования называется задачей стохастического программирования, когда А) только коэффициенты целевой функции могут принимать случайные значения, В) коэффициенты целевой функции и коэффициенты ограничений могут принимать случайные значения -: A– да, B– да -: A– да, B– нет +: А – нет, В – да -: A– нет, B- нет
I: S: Подавляющее большинство методов оптимизации позволяет находить -: только глобальные экстремумы… -: локальные экстремумы и глобальные экстремумы +: только локальные экстремумы -: нули целевой функции
I: S: По типу используемого математического аппарата выделяют модели (отметить два правильных варианта ответа): +: матричные +: оптимального программирования (линейного и нелинейного) -: равновесные -: нормативные
I: S: Количество ограничений СУММ (ahjХhj)<=Bh, h=(1,H), j=(1,n) в числовой модели оптимальной загрузки взаимозаменяемого оборудования равно: +: количеству видов оборудования -: количеству видов материалов -: количеству видов продукции
I: S: Количество ограничений СУММ (Xhj)>=Aj, h=(1,H), j=(1,n) в числовой модели оптимальной загрузки взаимозаменяемого оборудования равно: +: количеству видов продукции -: количеству видов материалов -: количеству видов оборудования
I: S: Левая часть ограничения СУММ (ahjxj)<=Bh, h=(1,H), j=(1,n) числовой модели оптимальной загрузки невзаимозаменяемого оборудования означает время, которое необходимо для производства: +: всех видов продукции на h-том виде оборудования -: единицы j-той продукции на h-том виде оборудования -: j-той продукции на h-том виде оборудования
I: S: Величина (ahj) в ограничении СУММ (ahjxj)<=Bh, h=(1,H), j=(1,n) числовой модели оптимальной загрузки невзаимозаменяемого оборудования означает время, которое необходимо для производства: +: единицы j-той продукции на h-том виде оборудования -: j-той продукции на h-том виде оборудования -: всех видов продукции на h-том виде оборудования
I: S: Ограничение по объему производимой продукции в обязательном порядке присутствует: +: в моделях оптимальной загрузки взаимозаменяемого оборудования -: в моделях оптимальной загрузки невзаимозаменяемого оборудования
I: S: В моделях смесевых задач в качестве заданных исходных параметров рассматривается (отметить два правильных варианта ответа) +: содержание качественных характеристик в единице исходных компонентов +: цена исходных компонентов -: количество исходных компонентов, которое входит в готовую смесь -: объем (количество) получаемой смеси
I: S: В моделях смесевых задач в качестве искомых переменных выступает: +: количество исходных компонентов, которое входит в готовую смесь -: содержание качественных характеристик в единице исходных компонентов -: цена исходных компонентов -: объем (количество) получаемой смеси
I: S: В моделях смесевых задач любого типа в обязательном порядке присутствует ограничение: +: по качественным характеристикам -: по объему ресурсов -: по объему выпускаемой продукции (смеси)
I: S: В качестве критерия оптимальности в моделях смесевых задач выступает: +: стоимость смеси -: максимальная загрузка оборудования по смешиванию -: максимальный объем продаж смеси в натуральном выражении
I: S: В моделях оптимального раскроя материалов в качестве заданных исходных параметров рассматривается: +: количество готовых изделий, которое необходимо получить в результате раскроя -: количество исходного сырья, которое требуется раскроить по каждому варианту раскроя -: количество исходного сырья, которое требуется получить в результате раскроя
I: S: В моделях оптимального раскроя материалов в качестве искомых переменных выступает: +: количество исходного сырья, которое требуется раскроить по каждому варианту раскроя -: количество готовых изделий, которое необходимо получить в результате раскроя -: отходы сырья, получаемые в результате раскроя
I: S: Максимальный объем продаж - это критерий оптимальности: +: локальный -: глобальный
I: S: Наиболее дефицитным является ресурс, который имеет двойственную оценку: +: наибольшую -: наименьшую -: нулевую
I: S: Для рассмотрения целесообразности включения в план нового изделия используются: (отметить три правильных варианта ответа) +: прибыль на единицу изделия +: двойственные оценки +: нормы затрат ресурсов на единицу изделия -: целевая функция -: количество ресурса
I: S: Ресурс недоиспользуется, если его двойственная оценка: +: равна нулю -: больше нуля -: является наибольшей по сравнению с двойственными оценками других ресурсов
I: S: Критерий оптимальности - это показатель, который выражает: +: предельную меру экономического эффекта решения -: суммарную меру экономического эффекта решения -: среднюю меру экономического эффекта решения
I: S: Двойственные оценки используемых в производстве трех видов ресурсов равны 2, 0, 4. Рассматривается вариант начала производства нового вида продукции. Затраты ресурсов на производство единицы нового вида продукции равны соответственно 15, 12, 7 ед.; прибыль от реализации единицы продукции - 63 ед. В этом случае производство нового вида продукции является: +: обоснованным, выгодным -: убыточным -: необходимы дополнительные данные
I: S: Целевая функция Zmax = СУММ(pjxj), j = (1,n) характеризует максимизацию выпуска продукции: +: в стоимостном выражении -: в натуральном выражении -: в условно-натуральном выражении
I: S: Целевая функция Zmax = СУММ(xj), j = (1,n) характеризует максимизацию выпуска продукции: +: в натуральном выражении -: в стоимостном выражении -: в натурально-стоимостном выражении
I: S: Целевая функция Zmin = СУММ(tjxj), j = (1,n) характеризует: +: минимизацию общей трудоемкости производимой продукции -: минимизацию использования конкретных видов ресурсов -: минимизацию затрат по производству конкретных видов продукции
I: S: Выражение СУММ(tijxj) <Ti, i = (1, m), j = (1,n) является ограничением: +: по затратам труда -: по материалам -: по объему продаж
I: S: Выражение СУММ(rijxj) <= Ri, i = (1, m), j = (1,n) является ограничением: +: по материалам -: по затратам труда -: по объему продаж
I: S: Выражение СУММ(pjxj) >= P, i = (1, m), j = (1,n) является ограничением: +: по объему продаж -: по затратам труда -: по материалам
I: S: Модели смесевых задач особенно актуальны в следующих отраслях (отметить три правильных варианта ответа): +: металлургии +: нефтехимической промышленности +: пищевой -: машиностроении -: текстильной
I: S: К смесевым относится задача составления: +: рационального питания -: рационального раскроя -: рационального использования ресурсов
I: S: Основная цель решения транспортной задачи (в том числе задачи оптимального развития и размещения производств): +: минимизация затрат на производство и перевозки продукции -: уменьшение количества пунктов назначения -: увеличение количества пунктов отправления -: минимизация количества перевозимого груза
I: S: Объемные ограничения в модели оптимизации производственной программы (отметить два правильных варианта ответа) - это ограничения: +: по объемам продукции на основе заключенных договоров +: по предполагаемому спросу на продукцию -: по имеющимся объемам ресурсов -: по качеству продукции
I: S: Заданные исходные параметры ресурсов модели оптимизации производственной программы (отметить два правильных варианта ответа): +: располагаемый фонд времени работы оборудования +: производительность работающего оборудования -: степень износа числящегося на балансе оборудования -: простои оборудования
I: S: Заданные исходные параметры ресурсов модели оптимизации производственной программы (отметить два правильных варианта ответа): +: установленный лимит сырья (материалов) +: норма расхода сырья (материалов) на производство единицы продукции -: среднесписочная численность работающих -: тарифная ставка
I: S: Левая часть ограничения СУММ(rijxj) <= Ri, i = (1, m), j = (1,n) числовой модели формирования оптимальной производственной программы означает: +: количество материала i-того вида, которое необходимо для производства всех j-тых видов продукции -: количество материала i-того вида, которое необходимо для производства j-того вида продукции -: количество материала i-того вида, которое необходимо для производства единицы j-того вида продукции
I: S: В качестве критерия оптимальности используется максимум выпуска продукции в условно-натуральном выражении в отраслях (отметить два правильных варианта ответа): +: пищевой +: перерабатывающих -: машиностроении
I: S: Путем применения экономико-математических моделей рационального использования ресурсов могут быть решены задачи (отметить три правильных варианта ответа): +: загрузки оборудования +: составления смесей +: рационального раскроя материалов -: оптимизации производственной программы -: размещения производства
I: S: Путем применения экономико-математических моделей рационального использования производственной мощности могут быть решены задачи (отметить два правильных варианта ответа): +: загрузки невзаимозаменяемого оборудования +: загрузки взаимозаменяемого оборудования -: рационального раскроя материалов -: рационального составления смесей
I: S: Путем применения экономико-математических моделей рационального использования материальных ресурсов могут быть решены задачи (отметить два правильных варианта ответа): +: рационального раскроя материалов +: рационального составления смесей -: загрузки взаимозаменяемого оборудования -: формирования производственной программы
I: S: Путем применения моделей загрузки взаимозаменяемого оборудования могут быть решены задачи, в которых: +: одни и те же операции можно выполнять на оборудовании с разной производительностью -: не допускаются разные варианты технологии обработки изделия
I: S: Путем применения экономико-математических моделей использования производственной мощности могут быть решены задачи (отметить два правильных варианта ответа): +: подбора оптимальной производственной программы, позволяющей наилучшим образом использовать имеющиеся мощности +: оптимального распределения работ по группам оборудования для выполнения заданной производственной программы с наименьшими затратами -: подбора оптимальной производственной программы, позволяющей наилучшим образом использовать имеющиеся трудовые ресурсы
I: S: Целевая функция моделей по рациональному составлению смесей: +: минимальная стоимость смеси -: минимальное количество компонентов -: максимум выпуска готовой продукции
V2. Линейное программирование.
I: S: Автором линейного программирования является: +: Л. Канторович -: Г. Фельдман -: В. Немчинов.
I: S: Ученый, который разработал метод линейного программирования и стал лауреатом Нобелевской премии: +: Л.В.Канторович. -: Н.Д.Кондратьев -: В.В.Новожилов
I: S: Какое уравнение называется характеристическим уравнением матрицы А: -: (E – A)*X = Y -: A*X = B +:
I: S: Множество n – мерного арифметического точечного пространства называется выпуклым, если: +: вместе с любыми двумя точками А и В оно содержит и весь отрезок АВ -: счетно и замкнуто -: равно объединению нескольких конечных множеств
I: S: Какая задача является задачей линейного программирования: -: управления запасами +: составление диеты -: формирование календарного плана реализации проекта
I: S: Задача линейного программирования называется канонической, если система ограничений включает в себя: -: только неравенства -: равенства и неравенства +: только равенства
I: S: Тривиальными ограничениями задачи линейного программирования называются условия: -: ограниченности и монотонности целевой функции +: не отрицательности всех переменных -: не пустоты допустимого множества
I: S: Если в задаче линейного программирования допустимое множество не пусто и целевая функция ограничена, то: -: допустимое множество не ограничено -: оптимальное решение не существует +: существует хотя бы одно оптимальное решение
I: S: Какое из следующих утверждений истинно? А) существуют задачи целочисленного линейного программирования, не имеющие допустимых решений даже в тех случаях, когда множество допустимых решений соответствующей линейной задачи не пусто В) не существует задач целочисленного линейного программирования, не имеющих допустимых решений в случаях, когда множество допустимых решений соответствующей линейной задачи не пусто -: A– нет, B- нет -: A– да, B– да -: A– нет, B– да +: А – да, В – нет
I: S: Булевское программирование – это целочисленное … +: линейное программирование, где переменные могут принимать всего лишь два значения - 0 и 1 -: нелинейное программирование, где переменные могут принимать всего лишь два значения - 0 и 1 -: квадратичное программирование, где переменные могут принимать всего лишь два значения - 0 и 1 -: линейное программирование, где переменные могут принимать всего лишь два значения - -1 и +1
I: S: Задача линейного программирования может рассматриваться как… +: частный случай задачи выпуклого программирования -: частный случай задачи дискретного программирования -: обобщение задачи выпуклого программирования -: частный случай задачи стохастического программирования
I: S: Задача коммивояжера относится к задачам -: квадратичного программирования -: выпуклого программирования -: математического анализа +: Булевского программирования
I: S: Область допустимых решений задачи линейного программирования имеет вид:
Тогда максимальное значение функции -: 26 -: 32 +: 30 -: 24
I: S: Область допустимых решений
Тогда максимальное значение функции -: C +: B -: D -: A
I: S: Область допустимых решений
Тогда максимальное значение функции -: 26 +: 24 -: 18 -: 12
I: S: Область допустимых решений
Тогда максимальное значение функции
-: C +: B -: A -: E
I: S: Область допустимых решений
Тогда минимальное значение функции -: – 16 -: – 18 -: – 22 +: – 34
I: S: Минимальное значение целевой функции
равно … -: – 2 +: – 6 -: 12 -: – 8
I: S: Максимальное значение целевой функции
равно … +: 22 -: 18 -: 24 -: 16
I: S: Максимальное значение целевой функции
равно … +: 14 -: – 1 -: 24 -: – 6
I: S: Минимальное значение целевой функции
равно … +: – 13 -: – 11 -: – 10 -: – 16
I: S: Область допустимых решений задачи линейного программирования имеет вид:
Тогда максимальное значение функции -: 18 -: 20 -: 23 +: 21
I: S: Максимальное значение целевой функции
равно… -: 6 -: 12 +: 18 -: 20
I: S: При использовании градиента необходимое условие экстремума записывается в виде… -: grad z(X)≤0 -: grad z(X)≠0 +: grad z(X)=0 -: grad z(X)≥0
I: S: Рекуррентная формула метода градиента для минимизации целевой функции имеет вид
-:
-:
I: S: Вектор-градиент в некоторой точке определяется как вектор, компонентами которого являются… -: прямые производные этой функции в точке +: частные производные первого порядка этой функции в точке -: частные производные второго порядка этой функции в точке -: частные производные третьего порядка этой функции в точке
I: S: Выделяются две группы методов нулевого порядка: +: детерминированные и случайные -: однопараметрические и многопараметрические -: конечные и асимптотические -: однокритериальные и многокритериальные
I: S: Градиентом функции n переменных z(X) называется вектор, компонентами которого являются… -: прямые производные первого порядка этой функции в точке -: частные производные третьего порядка этой функции в точке +: частные производные первого порядка этой функции в точке -: частные производные второго порядка этой функции в точке
I: S: Направление градиента в точке X совпадает с направлением -: знакопостоянства целевой функции в этой точке -: постоянства целевой функции в этой точке +: наискорейшего возрастания целевой функции в этой точке -: наискорейшего убывания целевой функции в этой точке
I: S: Симплекс-метод предназначен для решения задачи линейного программирования -: в стандартном виде +: в каноническом виде -: в тривиальном виде
I: S: Неизвестные в допустимом виде системы ограничений задачи линейного программирования, которые выражены через остальные неизвестные, называются: -: свободными +: базисными -: небазисными
I: S: Симплексный метод – это вычислительная процедура, основанная на принципе последовательного улучшения решений при переходе от одной базисной точки (базисного решения) к другой. При этом значение целевой функции: +: улучшается -: уменьшается -: ухудшается -: увеличивается
I: S: Базисным решением является одно из возможных решений, находящихся: -: в пределах области допустимых значений +: в вершинах области допустимых значений -: на границах области допустимых значений -: за пределами области допустимых значений
I: S: Симплекс-метод основан на проверке на оптимальность: -: ограничений симплекса -: области допустимых решений симплекса -: сторон симплекса +: вершины за вершиной симплекса
I: S: Симплекс это: -: выпуклый многоугольникв n- мерном пространстве с n вершинами не лежащими в одной гиперплоскости +: выпуклый многоугольникв n- мерном пространстве с n+1 вершинами не лежащими в одной гиперплоскости -: выпуклый многоугольникв n- мерном пространстве с n+1 вершинами лежащими в одной гиперплоскости -: выпуклый многоугольникв n- мерном пространстве с n вершинами не лежащими в одной гиперплоскости
I: S: Множество переменных, образующих единичную подматрицу, принимается за начальное базисное решение: -: значения этих переменных равны свободным членам. Все остальные вне базисные переменные не равны нулю. -: значения этих переменных равны нулю. Все остальные вне базисные переменные равны свободным членам. -: значения этих переменных равны нулю. Все остальные вне базисные переменные не равны нулю. +: значения этих переменных равны свободным членам. Все остальные вне базисные переменные равны нулю.
I: S: Как называются переменные двойственной задачи?
-: дополнительными переменными +: объективно обусловленными переменными -: объективно обусловленными оценками -: искусственными переменными
I: S: Транспортная задача формулируется следующим образом: Найти такие объемы перевозок для каждой пары «поставщик-потребитель», чтобы 1) мощности всех поставщиков были использованы полностью; 2) спрос всех потребителей был удовлетворен: -: 3) суммарные затраты на перевозки были минимальные +: 3) суммарные затраты на перевозки были максимальные -: 3) мощности всех поставщиков и мощности всех потребителей должны быть равны -: 3) мощности всех поставщиков должны быть больше мощностей всех потребителей
I: S: Целевая функция транспортной задачи обычно записывается так, что бы: -: суммарные затраты стремились к нулю +: суммарные затраты стремились к минимуму -: суммарные затраты стремились к максимуму -: суммарная прибыль стремилась к максимуму нулю
I: S: Ограничения транспортной задачи представляет собой: -: систему неравенств -: систему неравенств и уравнений -: область допустимых решений +: систему уравнений
I: S: Коэффициенты в системе ограничений транспортной задачи представляет собой: -: равны единице -: большие нуля +: равны единице или нулю -: меньше или равны нулю
I: S: Метод северо-западного угла предполагает планирование поставок в: +: верхнюю левую ячейку -: верхнюю правую ячейку -: нижнюю левую ячейку -: нижнюю правую ячейку
I: S: Транспортная задача
будет закрытой, если … -: -: +: -:
I: S: Транспортная задача
будет закрытой, если … +: -: -: -:
I: S: Транспортная задача
будет открытой, если… +: a =40, b =30 -: a =13, b =23 -: a =100, b =110 -: a =30, b =40
I: S: Транспортная задача будет закрытой, если
-: a=35, b=20 -: a=35, b=15 -: a=35, b=30 +: a=35, b=25
I: S: Пусть имеется два поставщика мощностью 80 и 90 и три потребителя мощностью 40; 50 и 60. Затраты на перевозки от первого поставщика к потребителям соответственно равны 2, 5, 6; от второго 4, 7, 3. Определите суммарные затраты на перевозки методом наименьших затрат. -: 620 +: 530 -: 760 -: 480
I: S: Пусть имеется два поставщика мощностью 80 и 90 и три потребителя мощностью 40; 50 и 60. Затраты на пере
|



 равно …
равно …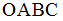 задачи линейного программирования имеет вид:
задачи линейного программирования имеет вид:
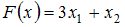 достигается в точке …
достигается в точке … равно …
равно … задачи линейного программирования имеет вид:
задачи линейного программирования имеет вид: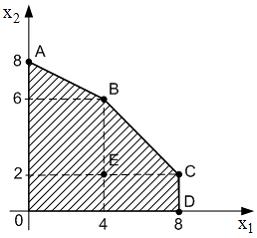
 равно …
равно … при ограничениях
при ограничениях
 при ограничениях
при ограничениях при ограничениях
при ограничениях
 при ограничениях
при ограничениях

 равно…
равно…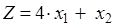 при ограничениях:
при ограничениях:
 +:
+: -:
-:


 ,
, 
 ,
, 
 ,
, 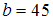
 ,
, 

 ,
,  ,
, 
 ,
,  ,
, 
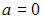 ,
,  ,
, 




