Механические колебания и волны.
1. Тиреотоксический криз 2. Достижение стойкого клинического и лабораторного эутиреоза с применением тиреостатиков (мерказолил, тирозол, пропицил), раствора Люголя, глюкокортикоидов при тяжелом тиреотоксикозе, истощении надпочечников и риске развития тиреотоксического криза. 3. А) Введение глюкокортикоидов- 100мг гидрокортизона в/в каждые 4 часа; Б) Тиреостатики (тирозол 100-120 мг/сут или пропицил 1000-1200мг/сут; В) 1% раствор Люголя (с натрием йодидом) в/в кап; Г) β-блокаторы (анаприлин 1-2 мг в/в); Д) дезинтоксикационная терапия в объеме 3 л в сут (р-р глюкозы, физ. Раствор); Е) седатики – фенобарбитал 0,05г – 2- 3р/сут
Краткие теоретические сведения Механические колебания и волны. 1.1. Дифференциальное уравнение гармонических колебаний имеет вид:
Решением этого уравнения является закон гармонических колебаний:
где 1.2. Скорость точки, совершающей гармонические колебания:
где 1.3. Ускорение точки, совершающей гармонические колебания:
где 1.4. Период и круговая частота свободных колебаний пружинного маятника:
где 1.5. Период и круговая частота малых свободных колебаний физического маятника:
где 1.6. Период и круговая частота малых свободных колебаний математического маятника:
где 1.7. Потенциальная энергия гармонических колебаний пружинного маятника:
1.8. Кинетическая энергия гармонических колебаний пружинного маятника:
1.9. Полная энергия гармонических колебаний пружинного маятника:
1.10. Дифференциальное уравнение затухающих колебаний пружинного маятника:
где 1.11. Решением дифференциального уравнения затухающих колебаний является закон затухающих колебаний:
где 1.12. Логарифмический декремент затухания:
1.13.Время релаксации:
1.14. Добротность:
1.15. Дифференциальное уравнение вынужденных колебаний:
где 1.16. Решение дифференциального уравнения для установившихся вынужденных колебаний:
где 1.17. Условие механического резонанса:
и амплитуда резонансных колебаний:
1.18. Связь длины
1.19. Скорость распространения упругих продольных волн в тонких стержнях:
где 1.20 Скорость распространения упругих волн в газах:
где
1.21. Уравнение плоской гармонической волны:
где
|

 .
.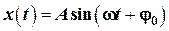 .
.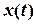 — отклонение колеблющейся величины от положения равновесия в момент времени t;
— отклонение колеблющейся величины от положения равновесия в момент времени t;  — амплитуда колебаний;
— амплитуда колебаний; 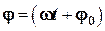 — фаза колебаний;
— фаза колебаний; 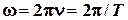 — циклическая (круговая) частота;
— циклическая (круговая) частота;  — период колебаний;
— период колебаний; 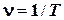 — частота;
— частота; 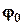 — начальная фаза колебаний.
— начальная фаза колебаний.  ,
,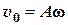 — амплитуда скорости.
— амплитуда скорости.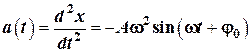
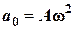 — амплитуда ускорения.
— амплитуда ускорения.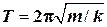 ,
, 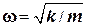 ,
, — масса груза;
— масса груза;  — жесткость (коэффициент упругости) пружины.
— жесткость (коэффициент упругости) пружины.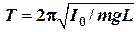 ,
,  ,
, — момент инерции маятника относительно оси вращения;
— момент инерции маятника относительно оси вращения;  — расстояние от оси вращения до центра тяжести маятника;
— расстояние от оси вращения до центра тяжести маятника; 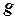 — ускорение свободного падения.
— ускорение свободного падения.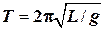 ,
, 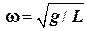 ,
,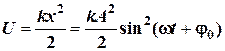 .
.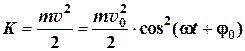 .
.
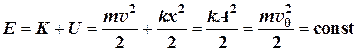 .
.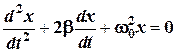 ,
, — коэффициент затухания;
— коэффициент затухания; 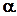 — коэффициент вязкого трения;
— коэффициент вязкого трения; 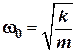 — круговая частота свободных колебаний маятника.
— круговая частота свободных колебаний маятника.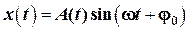 ,
,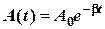 — амплитуда затухающих колебаний;
— амплитуда затухающих колебаний; 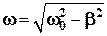 — круговая частота затухающих колебаний.
— круговая частота затухающих колебаний.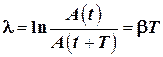 .
.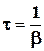 .
.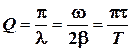 .
.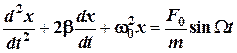 ,
, — циклическая частота вынуждающей силы,
— циклическая частота вынуждающей силы,  — максимальное значение (амплитуда) внешней силы.
— максимальное значение (амплитуда) внешней силы.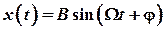 ,
,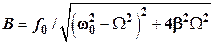 — амплитуда вынужденных колебаний;
— амплитуда вынужденных колебаний; 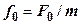 ;
; 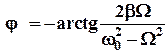 — сдвиг фазы между смещением
— сдвиг фазы между смещением 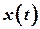 и внешней силой.
и внешней силой.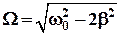 ,
,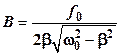 .
. и скорости
и скорости  распространения волны:
распространения волны: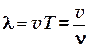 .
.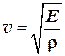 ,
, — модуль Юнга;
— модуль Юнга;  — плотность материала стержня.
— плотность материала стержня.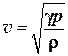 ,
,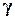 — показатель адиабаты;
— показатель адиабаты;  — давление;
— давление;  ,
,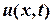 — смещение частиц среды в точке
— смещение частиц среды в точке  в момент времени
в момент времени  ;
; 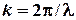 — волновое число;
— волновое число; 


