Примеры решения задач. 1. Маятник колеблется по закону
1. Маятник колеблется по закону Решение: Из закона движения маятника получаем, что в момент времени
Скорость колебаний маятника определяется по формуле:
и в момент времени
Разделив уравнение (1) на уравнение (2), получим:
Отсюда начальная фаза колебаний:
Амплитуду колебаний находим из уравнения (1):
Ответ: 2. Вывести дифференциальное уравнение малых свободных колебаний физического маятника, а также формулы периода и круговой частоты этих колебаний. Решение: Физический маятник — твердое тело массой
Для малых колебаний
По второму закону Ньютона для вращательного движения:
Отсюда получаем дифференциальное уравнение малых свободных колебаний физического маятника:
Это уравнение тождественно уравнению гармонических колебаний:
Следовательно, малые колебания физического маятника происходят по гармоническому закону:
с собственной круговой частотой
3. Период затухающих колебаний равен Решение: По определению логарифмический декремент затухания равен:
Отсюда получаем коэффициент затухания:
Добротность колебаний равна:
а время релаксации:
Ответ:
4. Упругая волна распространяется со скоростью Решение: Скорость упругих волн в тонком твердом стержне определяется по формуле:
где Отсюда находим модуль Юнга (модуль упругости) для стержня:
Ответ: 5. Найти массу воздуха при температуре 27°С, давлении 1 атм и объеме 72 м3 . Решение: Уравнение состояния идеального газа (уравнение Менделеева ─ Клапейрона):
где Отсюда получаем формулу для расчета массы воздуха:
Абсолютная температура Т = t˚;C + 273 K = 27˚C + 273 K = 300 K, 1 атм = 1,013∙105 Па. Подставив численные данные в расчетную формулу, получаем:
Ответ: 6. Определить концентрацию молекул водорода, если среднеквадратичная скорость его молекул u = 900 м/с, давление Решение: Связь между давлением и средней кинетической энергией
где
где Массу молекулы найдем, разделив молярную массу
Подставив (3) в (2), а затем (2) в (1), получим:
Отсюда
Ответ: 7. При изобарном нагревании 10 моль гелия было затрачено 2078 Дж тепла. Найти работу, изменение внутренней энергии и температуры гелия. Решение: Количество теплоты
где
Подставив (2) в (1), найдем изменение температуры:
Работа при изобарном нагревании определяется по формуле:
Изменение внутренней энергии найдем с помощью первого закона термодинамики:
Ответ: А = 831 Дж; Δ U = 1247 Дж; Δ T = 10 K. 8. Определить КПД идеального двигателя и температуру холодильника, если за счет каждого килоджоуля теплоты, полученного от нагревателя, двигатель совершает работу 350 Дж. Температура нагревателя 227 °С. Решение: Коэффициент полезного действия (КПД) теплового двигателя равен: где Численный расчет:
КПД идеального теплового двигателя определяется по теореме Карно: где T х = T н(1─ηmax). Абсолютная температура нагревателя:
Численный расчет:
Ответ: 9. Найти среднюю длину свободного пробега молекулы кислорода, если плотность газа равна 0,064 кг/м3.
Решение: Средняя длина свободного пробега молекул газа:
где Плотность газа равна: где Отсюда находим концентрацию молекул: Численный расчет:
Ответ: 10. Найти коэффициент теплопроводности воздуха при давлении Решение: Коэффициент теплопроводности определяется по формуле:
где Плотность воздуха определяем из уравнения Менделеева-Клапейрона:
где
Молярная теплоемкость воздуха при постоянном объеме:
где i = 5― число степеней свободы молекулы воздуха. Средняя арифметическая скорость молекул:
Средняя длина свободного пробега молекул газа:
где Плотность газа равна: где
и среднюю длину свободного пробега молекул:
Подставив (2), (3), (4), (5) в формулу (1), получим:
Ответ:
|

 . В момент времени
. В момент времени  = 0 смещение маятника от положения равновесия
= 0 смещение маятника от положения равновесия  = 5 см, а скорость
= 5 см, а скорость 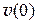 = 10 см/с. Определить амплитуду и начальную фазу колебаний, если круговая частота
= 10 см/с. Определить амплитуду и начальную фазу колебаний, если круговая частота  = 2 рад/с.
= 2 рад/с. . (1)
. (1) ,
, . (2)
. (2) .
. .
.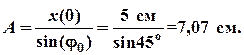
 ,
,  .
. , с моментом инерции
, с моментом инерции  , имеющее ось вращения
, имеющее ось вращения  , расположенную выше центра тяжести
, расположенную выше центра тяжести  .
.
 Тело совершает вращательно–колебательные движения под действием момента силы тяжести, приложенной в центре тяжести
Тело совершает вращательно–колебательные движения под действием момента силы тяжести, приложенной в центре тяжести  .
.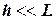 ,
,  . Таким образом,
. Таким образом,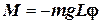 .
.
 .
. .
. .
.
 и периодом
и периодом 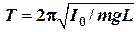 .
. = 2 с, логарифмический декремент
= 2 с, логарифмический декремент  = 0,2. Определить коэффициент затухания, добротность и время релаксации колебаний.
= 0,2. Определить коэффициент затухания, добротность и время релаксации колебаний. .
.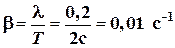 .
. ,
, .
.
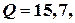

 = 5300 м/с в стержне плотностью
= 5300 м/с в стержне плотностью  = 7,8 г/см3. Найти модуль упругости (модуль Юнга) стержня.
= 7,8 г/см3. Найти модуль упругости (модуль Юнга) стержня.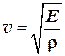 ,
, — модуль Юнга;
— модуль Юнга; 

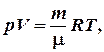
 — давление;
— давление;  — объем;
— объем;  — универсальная газовая постоянная.
— универсальная газовая постоянная.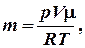


 поступательного движения молекулы идеального газа (основное уравнение молекулярно-кинетической теории идеальных газов):
поступательного движения молекулы идеального газа (основное уравнение молекулярно-кинетической теории идеальных газов):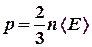 , (1)
, (1)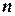 — концентрация молекул. Средняя кинетическая энергия поступательного движения молекулы идеального газа:
— концентрация молекул. Средняя кинетическая энергия поступательного движения молекулы идеального газа: , (2)
, (2) ― масса одной молекулы;
― масса одной молекулы;  — средняя квадратичная скорость молекулы.
— средняя квадратичная скорость молекулы. водорода на число молекул в одном моле
водорода на число молекул в одном моле  (постоянную Авогадро):
(постоянную Авогадро): . (3)
. (3)


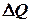 , необходимое для нагревания ν;молейгаза в изобарном процессе, можно найти по формуле:
, необходимое для нагревания ν;молейгаза в изобарном процессе, можно найти по формуле: (1)
(1)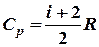 — молярная теплоемкость газа в изобарном процессе; i — число степеней свободы молекулы; R ― универсальная газовая постоянная,
— молярная теплоемкость газа в изобарном процессе; i — число степеней свободы молекулы; R ― универсальная газовая постоянная,  — изменение температуры. для гелия i = 3 и, следовательно,
— изменение температуры. для гелия i = 3 и, следовательно,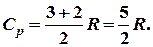 (2)
(2)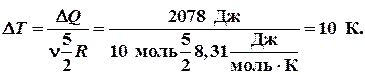
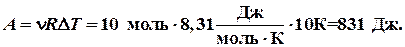


 — теплота, полученная двигателем от нагревателя;
— теплота, полученная двигателем от нагревателя;  — работа, совершенная двигателем.
— работа, совершенная двигателем.
 ,,
,,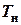 — температура нагревателя;
— температура нагревателя;  — температура холодильника. Отсюда находим температуру холодильника:
— температура холодильника. Отсюда находим температуру холодильника:





 — эффективный диаметр (эффективный диаметр молекулы кислорода находим в справочной таблице: d = 0,29 нм);
— эффективный диаметр (эффективный диаметр молекулы кислорода находим в справочной таблице: d = 0,29 нм); 
 — масса молекулы;
— масса молекулы; 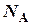 — постоянная Авогадро.
— постоянная Авогадро.

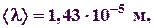
 , (1)
, (1) — плотность;
— плотность;  — молярная теплоемкость при постоянном объеме;
— молярная теплоемкость при постоянном объеме;  — средняя арифметическая скорость;
— средняя арифметическая скорость;  — средняя длина свободного пробега молекул воздуха.
— средняя длина свободного пробега молекул воздуха. (2)
(2)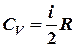 , (3)
, (3) (4)
(4)

 (5)
(5)




