Механическое движение
Вращательное Колебательное Линейная скорость: υ = ω· Α Амплитуда скорости: υm = ω·Α Центростремительное ускорение:
Вывод:Проекция ускорения гармонически колеблющегося тела прямо пропорциональна смещению с обратным знаком. Если:
IV. Задачи: 1. Точка совершает гармонические колебания с амплитудой 0,15 м, частотой 25 Гц и начальной фазой π/2. Записать закон изменения проекции скорости, координаты и проекции ускорения этой точки, построить графики соответствующих зависимостей. 2. Точка совершает гармонические колебания вдоль прямой линии. При движении между крайними положениями средняя скорость оказалась равной 4 м/с. Найдите максимальную скорость на этом участке. 3. Точка, совершающая гармонические колебания, в некоторый момент времени имеет смещение, скорость и ускорение, равные соответственно 0,04 м, 0,05 м/с, 0,8 м/с. Чему равны амплитуда и период колебаний точки? Каковы максимальная скорость и ускорение точки?
V. Конспект 1. Попытайтесь совершить простое гармоническое движение, двигаясь взад и вперед по некоторому отрезку пути. Наклон вашего туловища вдоль направления движения прямо пропорционален вашему ускорению. 2. Сравните формулы для смещения, скорости и ускорения при прямолинейном равноускоренном движении и соответствующие формулы для гармонических колебаний. В чем сходство и различие между ними?
"Сотри случайные черты – И ты увидишь! Мир прекрасен";. А. Блок
Урок 81/4. СОБСТВЕННЫЕ (СВОБОДНЫЕ) ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ
ЦЕЛЬ УРОКА: Показать, что собственные колебания пружинного и нитяного маятников – гармонические. Вывести формулы для определения периода колебаний и смещения.
ТИП УРОКА: Комбинированный. ОБОРУДОВАНИЕ: Набор пружинный с держателями, демонстрационный секундомер, демонстрационный пружинный маятник, набор грузов, электродвигатель, диск вращающийся с принадлежностями, демонстрационный нитяной маятник.
ПЛАН УРОКА: 1. Вступительная часть 1-2 мин 2. Опрос 10 мин 3. Объяснение 25 мин 4. Закрепление 5 мин 5. Задание на дом 2-3 мин II. Опрос фундаментальный: Скорость и ускорение при гармонических колебаниях. Задачи: 1. Точка совершает колебания вдоль оси х по закону: х = 0,05 м·cos π·t, где t в секундах. Определите амплитуду, период, максимальную скорость, максимальное ускорение и начальную фазу колебаний. Постройте примерный график проекции ускорения от времени. 2. Шар положен на край гладкого стола, плоскость которого перпендикулярна к отвесу. Определите период его малых колебаний. Если прорыть в Земле тоннель между двумя городами, то время движения поезда между ними составит 84 минуты. 3. Жидкость плотности ρ; в U – образной трубке смещают из положения равновесия на расстояние х. Масса жидкости m, сечение трубки S. Если не учитывать трение, то каким будет период ее колебаний? 4. Точка совершает гармонические колебания с амплитудой 5 см и циклической частотой 5 с-1. Найдите величину ускорения точки в те моменты, когда ее скорость равна 15 см/с. 5. Груз на пружине оттягивают на 10 см от положения равновесия и отпускают. На каком расстоянии от положения равновесия скорость груза будет равна половине максимальной, ускорение груза будет равно половине максимального? Вопрос: Что можно определить по графику колебаний? В одинаковых или разных фазах находятся крылья летящей птицы? А руки человека при ходьбе? III. Сравните уравнение движения гармонических колебаний с уравнением движения пружинного или математического маятников. αх = −ω2 х; αх = −ω2оп х; αs = −ω2ом Ѕ. Вывод: При одинаковых циклических частотах и амплитудах собственные колебания маятников и гармонические колебания происходят по одному и тому же закону. Сравнение колебаний тени шарика, совершающего равномерное движение по окружности, с колебаниями пружинного и нитяного маятников. Вывод:Собственные колебания пружинного и нитяного маятников гармонические. х = А cos (ω t +φ0)
Кто задает амплитуду колебаний, начальную фазу, период колебаний? По какому закону происходят колебания маятников? Как определить смещение маятников в любой момент времени? Частота собственных колебаний не зависит от способа возбуждения, а определяется исключительно свойствами самой системы. Маятниковые часы (Христиан Гюйгенс, ошибка в измерении времени 10 секунд в сутки). IV. Задачи: 1. Изготовить нитяной маятник, колебания которого будут происходить по закону: х = 0,1 м cos (πt + π/2). 2. Таракан массой 0,3 г попал в сеть к пауку. Паутина колеблется с частотой 15 Гц. Определите коэффициент жесткости паутины. С какой частотой будет колебаться паутина, если в нее попадет насекомое массой 0,1 г? 3. На пружине жесткости 4. К вертикальной пружине подвесили груз массой 200 г, при этом она удлинилась на 5 см. Каким будет период колебаний груза на пружине? 5. Для измерения массы космонавта на орбитальной станции используется подвижное сиденье известной массы m0, прикрепленное к пружине. При одной и той же начальной деформации (сжатии) пружины пустое сиденье возвращается в исходное состояние через время t0, если же на сиденье находится космонавт - через время t > t0. Какова масса космонавта? 6. Летящее горизонтально тело массы m попадает в тело массы 2m подвешенное на нити длиной l, и прилипает к нему. Найти период колебаний и максимальный угол отклонения нити от вертикали, если скорость первого тела была υ. 7. Груз осторожно прикрепляют к концу свободно висящей пружины. Когда груз освобождают, он опускается на 30 см вниз, а затем идет вверх. Чему равна амплитуда и период колебаний груза? Вопросы: Изменится ли период колебаний качелей, если вместо одного человека на качели сядут двое? Тело массой 200 г совершает гармонические колебания на пружине по закону: Сохранится ли период колебаний часов-ходиков, если их с Земли перенести на Луну? За одно и то же время первый математический маятник совершает одно колебание, а второй - три. Во сколько раз длина первого маятника больше длины второго маятника? В кабине лифта на нити, подвешенной к потолку, колеблется небольшой груз. Как будет двигаться груз относительно лифта, если в какой-то момент времени лифт начнет свободно падать? Используя эффект отталкивания одноименных магнитных полюсов, можно изготовить нитяной маятник с большим периодом колебаний. Как это сделать? Имеются два маятника. Период одного из них известен. Как проще всего узнать период другого? Покажите, что конический и математический маятники одинаковой длины имеют равные периоды колебаний. Почему жонглер, поставив на нос длинный шест, может двигаться с ним по сцене? Почему такое нельзя сделать с карандашом? Груз на легком стержне − тот же нитяной маятник. Как с помощью такого маятника доказать, что его период колебаний зависит от ускорения свободного падения?
V. § 56. Упр. 32. Лабораторная работа № 8. 1. Используя резинки от авиамоделей и металлическую пуговицу, изготовьте горизонтальный пружинный маятник и определите период его свободных колебаний. Выясните зависимость периода колебаний этого маятника от массы груза и жесткости резины. 2. В литературе описаны маятниковые часы, которые сохраняют точность хода при любой температуре. Они сделаны в виде тонкой трубки, заканчивающейся резервуаром ее ртутью. В чем преимущества такого устройства маятника? Предложите свою конструкцию часов, сохраняющих точность хода при любой температуре. 3. К одному концу упругой стальной линейки прикреплен груз, а другой конец ее жестко зафиксирован так, что линейка вертикальна. Отклоняя груз, вызывают его колебания. Один раз опыт проводят при верхнем положении груза, а другой - при нижнем положении. Объясните, почему при примерно одинаковой амплитуде периоды колебаний заметно отличаются.
"Точная наука немыслима без меры";. Д. И. Менделеев
ЦЕЛЬ РАБОТЫ: Измерить ускорение свободного падения в данной местности. ТИП УРОКА: Лабораторная работа. ОБОРУДОВАНИЕ: Шарик с отверстием, нить, штатив с муфтой и кольцом, секундомер. ПЛАН РАБОТЫ:
|

 = ω2·Α Амплитуда ускорения:
= ω2·Α Амплитуда ускорения: 
 .
.
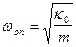


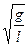
 подвешен груз массы m. Показать, что вертикальные колебания такого пружинного маятника гармонические и найти их период.
подвешен груз массы m. Показать, что вертикальные колебания такого пружинного маятника гармонические и найти их период. . Найдите жесткость пружины.
. Найдите жесткость пружины. Урок 82/5. ИЗМЕРЕНИЕ УСКОРЕНИЯ СВОБОДНОГО ПАДЕНИЯ
Урок 82/5. ИЗМЕРЕНИЕ УСКОРЕНИЯ СВОБОДНОГО ПАДЕНИЯ


