Эдгар По

Урок 73/2. ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ

 

ЦЕЛЬ УРОКА: Познакомить учащихся с колебаниями тени шарика, совер­шающего равномерное движение по окружности. Получить уравнение гармонических колебаний.

ТИП УРОКА: Комбинированный.

ОБОРУДОВАНИЕ: Диск вращающийся, электродвигатель, проекционный аппарат.

ПЛАН УРОКА:

1. Вступительная часть 1-2 мин

2. Опрос 10 мин

3. Объяснение 25 мин

4. Закрепление 5 мин

5. Задание на дом 2-3 мин

II. Опрос фундаментальный:

1. Основные понятия теории колебаний.

2. Уравнение движения пружинного маятника.

3. Уравнение движения математического маятника.

Задачи:

Записать уравнение колебательного дви­жения с параметрами: А = 5 см, Т = 2 c. В начальный момент времени смещение равно нулю. Построить гра­фик.

Самка беззубки откладывает каждые 50 с по яйцу, общее их количество может достигать 400 тысяч. Определите период и частоту откладывания яиц, и продолжительность этого процесса.

Вопросы:

Можно ли считать математический маятник моделью?

Какие из величин, описывающих свободные колебания, изменяются во времени: частота, период, амплитуда, смещение, скорость, ускорение, импульс?

Как называют график колебаний сердца, Земли, колеблющегося тела?

Каким образом можно записать колебания нитяного маятника (осциллограмма или график колебаний)?

Количество сердцебиений у человека за один год около 36800000. Какова частота пульса?

Нить с одинаковыми грузами на концах перекиньте через блок. Почему нарушается равновесие, если один из грузов отклонить от вертикали?

 

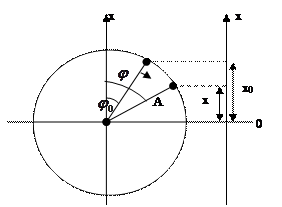III. Демонстрация колебаний тени шарика, совершаю­щего равномерное движение по окружности. Отметить на доске положение равновесия, амплитуду колебаний, смещение в разные моменты времени. Является ли смещение функцией времени? Можно ли для данного колеба­тельного движения решить основную задачу механики, т.е. найти урав­нение, с помощью которого можно будет определять смещение тени шарика в любой момент времени? Да!

Механическое движение

Вращательное Колебательное

А – радиус – амплитуда

X – проекция – смещение

φ₀ − начальный угол − начальная фаза

φ − угол поворота − фаза

Т − период обращения − период колебаний

ω − угловая скорость − циклическая частота

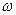Пример: n = 10 об/с, = 20π рад/с. ν = 10 Гц, = 20π (1/с)

X = A cosφ = A cos (ωt+φ₀)

 

По формуле можно определить смещение гармонически колеблющегося тела в любой момент времени.

Вопрос: Какое движение совершает проекция радиуса – вектора на ось Y?