Свободные колебания маятников
ИССЛЕДОВАНИЕ СВОБОДНЫХ И ВЫНУЖДЕННЫХ КОЛЕБАНИЙ СИСТЕМЫ С ДВУМЯ СТЕПЕНЯМИ СВОБОДЫ
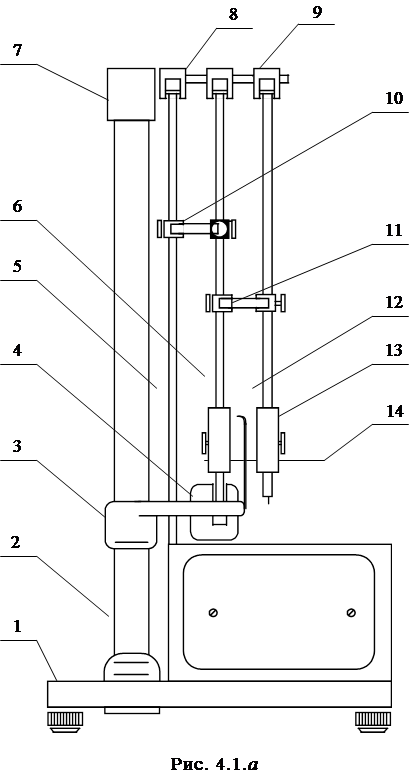
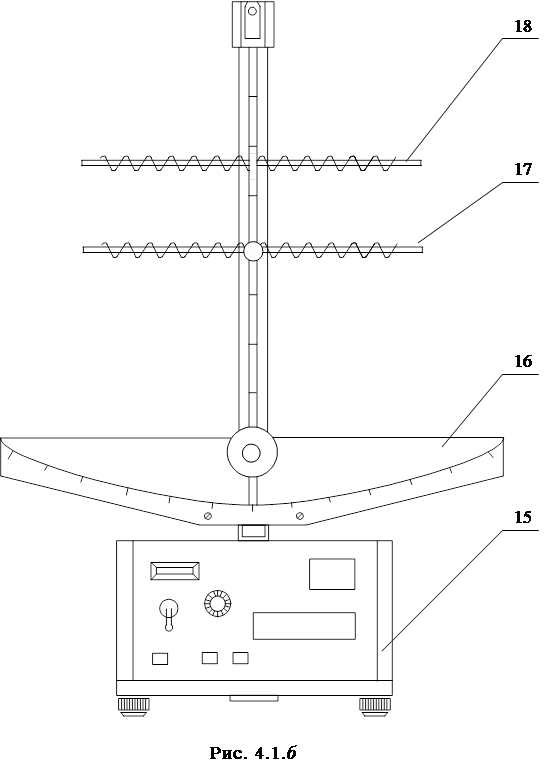
Свободными называются колебания, происходящие в системе в отсутствии внешних сил. Два маятника, связан-ные упругой связью и обладающие двумя степенями свобо-ды, представляют собой колебательную систему, в которой может происходить перераспределение энергии. Число сте-пеней свободы – это минимальное число независимых ко-ординат, с помощью которых можно полностью описать состояние системы. В данной работе такая система реали-зована (рис. 4.1. а,б) в виде двух маятников 13, 14 с регу-лируемыми параметрами (длина, вес груза), связанных с по-мощью двух одинаковых пружин 17 и C-образной обоймы 11, закрепленной на стержне второго (более удаленного от наблюдателя) маятника 6. Пружины соединяют оконечные участки обоймы 11 со стержнем первого (более близкого к наблюдателю) маятника 12. Углы отклонения обоих маят-ников от положения равновесия будем считать положи-тельными при смещении маятников против движе
ния часо-вой стрелки.
Каждый маятник участвует в периодическом вращатель-ном движении, которое может быть описано уравнением движения вращающегося тела (второй закон Ньютона):
где
Учитывая схему опыта (рис. 4.2), запишем уравнения движения в скалярном виде:
Учтем, что при малых углах Тогда сила упругости равна
Заметим, что ошибки здесь нет, т.к. второй маятник от-клонен в противоположную сторону, Тогда взаимосвязь между моментами сил, действующими на первый и второй маятники, описывается следующими со-отношениями:
где
Уравнения движения маятников, учитывая соотношение (4.1), имеют следующий вид:
Решение системы уравнений (4.3) существенно упро-щается, если ограничиться следующими условиями прове-дения опытов:
При этом
С учетом принятых обозначений, складывая и вычитая уравнения системы (4.3), получаем:
Каждое из уравнений (4.4) описывает гармонические ко-лебания с частотами Решения уравнений (4.4) имеют вид:
где
Рассмотрим три основных случая колебаний: синфазные (первая мода), когда в начальный период оба маятника от-клонены на одинаковый угол
При синфазных колебаниях начальные условия при
Подставляя (4.7) в формулу (4.5) и решая систему урав-нений, находим:
Таким образом, влияние связи при данном виде колеба-ний исчезает и длительности периодов колебаний маятни-ков имеют одинаковую величину и приближаются, в преде-лах точности эксперимента, к длительности периода мате-матического маятника такой же длины:
Встречные колебания характеризуются следующими на-чальными условиями (при
Подставляя (4.9) в (4.5), находим:
Наличие связи между маятниками в этом случае уже су-щественно, как следует из анализа соотношения (4.6) для
Биения возникают при следующих начальных условиях:
В этом случае решение системы уравнений (4.5) имеет вид:
Введем следующие обозначения:
Тогда соотношения (4.12) принимают следующий вид:
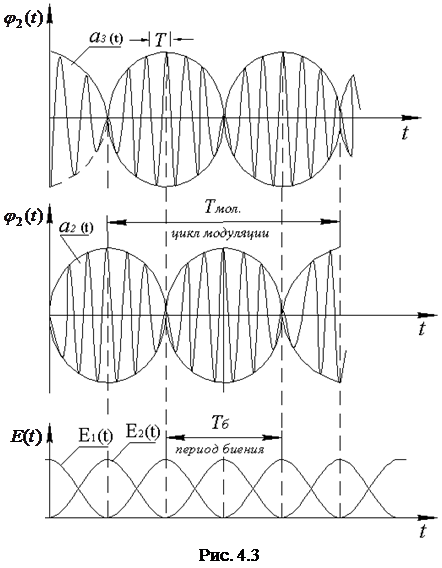
Из анализа соотношений (4.13) следует, что они пред-ставляют собой гармонические колебания с частотой, ам-плитуда и фаза которых не остаются постоянными через про-межутки времени, равные произвольному целому числу пе-риодов. Колебания подобного типа широко используются в электросвязи, где их называют модулированными. Модуля-ция – это изменение параметров колебаний с частотами, зна-чительно меньшими частоты самих колебаний (
где
(4.15)
При соблюдении условия
амплитуды колебаний
а амплитудные значения колебаний изменяются в пределах от Так как энергия гармонических колебаний пропорцио-нальна квадрату амплитуды, то, как показано на рис. 4.3, происходит периодическая передача энергии от одного маят-ника к другому. Длительность одного цикла передачи энер-гии от одного маятника к другому и обратно называется пе-риодом биений (
Найдем зависимости, определяющие энергию каждого из маятников, полагая амплитуды
где
Потенциальная энергия каждого из маятников определя-ется следующими соотношениями:
Полная энергия каждого из маятников равна соответст-венно:
Cложив соотношения (4.20), получим выражение для полной энергии двух маятников:
Разность энергий двух маятников с учетом соотношения
равна
Система уравнений (4.21) и (4.22) позволяет представить соотношение для полной энергии каждого из маятников в следующем виде:
Из анализа соотношений (4.21) и (4.23) следует, что пол-ная энергия системы остается с течением времени постоян-ной. Вместе с тем, имеет место передача энергии от одного маятника к другому с частотой биений, равной
Соотношение (4.24) можно записать в следующем виде:
следовательно,
При прочих начальных условиях движение маятников опи-сывается сложными формулами, вид которых существенно зависит от условий связи маятников.
|

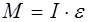 , (4.1)
, (4.1) – суммарный момент сил;
– суммарный момент сил;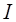 – момент инерции маятника;
– момент инерции маятника;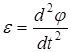 – угловое ускорение;
– угловое ускорение;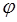 – угловое смещение;
– угловое смещение;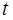 – текущее время.
– текущее время.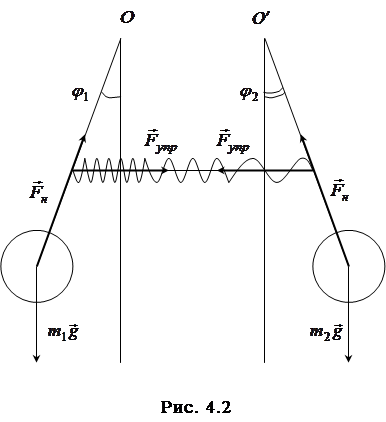
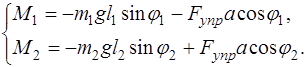
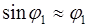 и
и 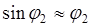 ;
; 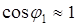 и
и 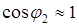 . Момент силы натяжения нити
. Момент силы натяжения нити  равен нулю.
равен нулю.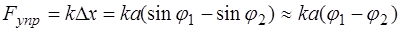 .
.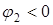 .
.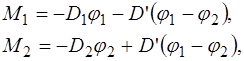 (4.2)
(4.2)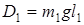 ;
; 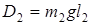 ;
; 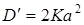 ;
;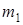 ,
, 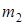 – массы грузов первого и второго маятников соот-ветственно (13, 14);
– массы грузов первого и второго маятников соот-ветственно (13, 14);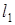 ,
, 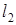 – расстояния от оси вращения до центров масс пер-вого и второго грузов;
– расстояния от оси вращения до центров масс пер-вого и второго грузов;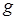 – ускорение свободного падения тел;
– ускорение свободного падения тел;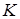 – коэффициент жесткости одной из двух одинаковых пружин (17);
– коэффициент жесткости одной из двух одинаковых пружин (17);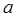 – расстояние от оси вращения до точки крепления пружин на стержне первого (12) маятника (А). На таком же расстоянии от оси должна быть укреплена обойма на стерж-не второго (6) маятника (В);
– расстояние от оси вращения до точки крепления пружин на стержне первого (12) маятника (А). На таком же расстоянии от оси должна быть укреплена обойма на стерж-не второго (6) маятника (В); 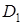 ,
, 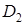 ,
, 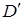 – определяются массой и геометрией каждого маятника.
– определяются массой и геометрией каждого маятника.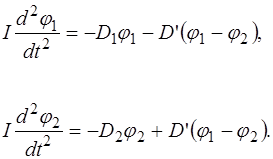 (4.3)
(4.3)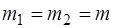 ;
; 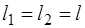 .
.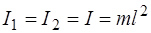 ;
; 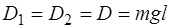 .
.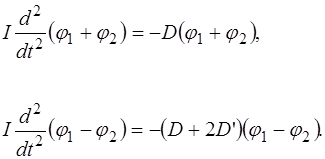 (4.4)
(4.4) ,
,  .
.
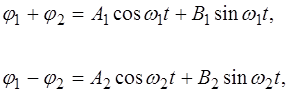 (4.5)
(4.5) ,
, 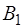 ,
, 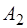 ,
, 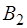 – постоянные коэффициенты, определяе-мые из начальных условий. Меньшую из частот
– постоянные коэффициенты, определяе-мые из начальных условий. Меньшую из частот  ,
, 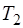 рассчитываются по следующим формулам:
рассчитываются по следующим формулам: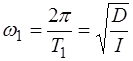 ;
; 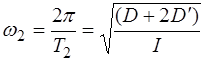 . (4.6)
. (4.6)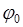 относительно положения равновесия; встречные колебания (вторая мода), когда в ис-ходном положении оба маятника отклонены от положения равновесия на одинаковые углы (
относительно положения равновесия; встречные колебания (вторая мода), когда в ис-ходном положении оба маятника отклонены от положения равновесия на одинаковые углы (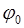 ), но в разные стороны; и биения, когда начальное смещение одного из маятников равно нулю, а величины собственных частот маятников име-ют близкие значения, т.е.
), но в разные стороны; и биения, когда начальное смещение одного из маятников равно нулю, а величины собственных частот маятников име-ют близкие значения, т.е.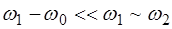 .
.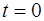 имеют следующий вид:
имеют следующий вид: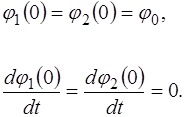 (4.7)
(4.7)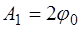 ;
; 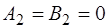 ;
;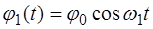 ;
; 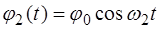 .
.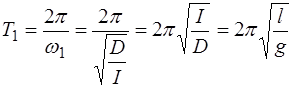 . (4.8)
. (4.8)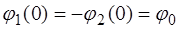 ,
,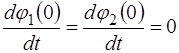 . (4.9)
. (4.9)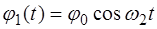 ;
; 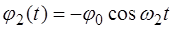 .
.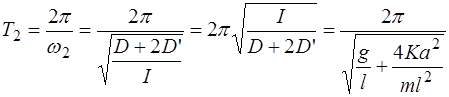 . (4.10)
. (4.10)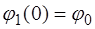 ;
; 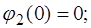
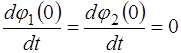 . (4.11)
. (4.11)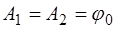 ;
; 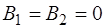 ;
;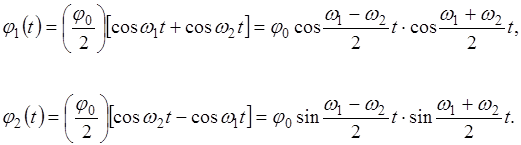 (4.12)
(4.12)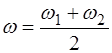 – средняя частота колебаний маятника;
– средняя частота колебаний маятника;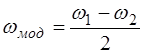 – частота "модуляции".
– частота "модуляции".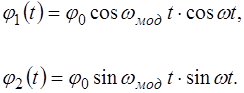 (4.13)
(4.13)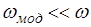 ). В зависимости от вида основного измеряемого параметра раз-личают амплитудную, частотную и фазовую модуляции. В рассматриваемом случае имеют место амплитудно-модули-рованные колебания, что представляется более наглядным при следующей форме записи соотношений (4.13):
). В зависимости от вида основного измеряемого параметра раз-личают амплитудную, частотную и фазовую модуляции. В рассматриваемом случае имеют место амплитудно-модули-рованные колебания, что представляется более наглядным при следующей форме записи соотношений (4.13):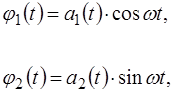 (4.14)
(4.14)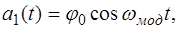
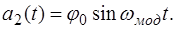
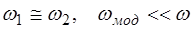
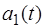 и
и 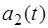 относительно медленно изменяются в течение нескольких колебаний с частотой
относительно медленно изменяются в течение нескольких колебаний с частотой  , т.е. уравнения (4.14) соответствуют почти гармоническим колебаниям. При этом каждый из маятников совершает колебания с периодом
, т.е. уравнения (4.14) соответствуют почти гармоническим колебаниям. При этом каждый из маятников совершает колебания с периодом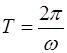 (4.16)
(4.16) до
до 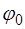 , причем фазы изменений амплитуд, как показано на рис. 4.3, отличаются на
, причем фазы изменений амплитуд, как показано на рис. 4.3, отличаются на 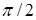 .
.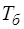 ).
).
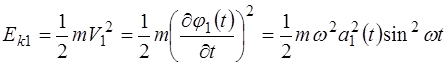 . (4.17)
. (4.17)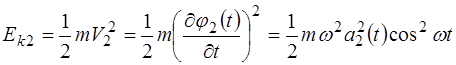 , (4.17')
, (4.17')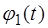 и
и 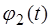 описываются соотношениями (4.14), а зна-чения
описываются соотношениями (4.14), а зна-чения 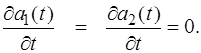 (4.18)
(4.18)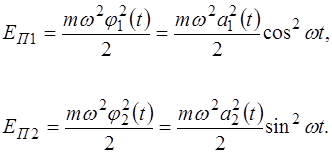 (4.19)
(4.19)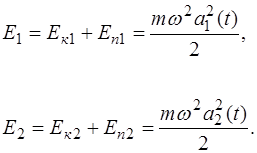 (4.20)
(4.20)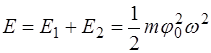 . (4.21)
. (4.21)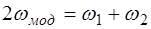
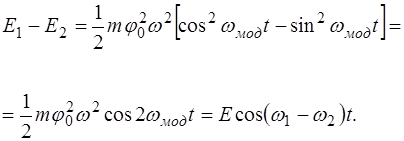 (4.22)
(4.22)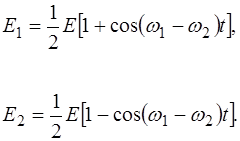 (4.23)
(4.23)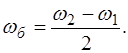 (4.24)
(4.24)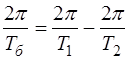 ,
,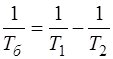 . (4.25)
. (4.25)


