МЕТОДИЧЕСКИЕ И ТЕОРЕТИЧЕСКИЕ ОСНОВЫ РАБОТЫ. Продольные звуковые волны в газах и металлах пред-ставляют собой периодические чередования сжатий и раз-режений в соответствующей среде
30. Укажите возможные причины несовпадения  и и  ; сравните величину ; сравните величину  и величины относительных ошибок, вычисленных в вопросах 27 и 29.
ОПРЕДЕЛЕНИЕ СКОРОСТИ РАСПРОСТРАНЕНИЯ ПРОДОЛЬНЫХ ЗВУКОВЫХ ВОЛН и величины относительных ошибок, вычисленных в вопросах 27 и 29.
ОПРЕДЕЛЕНИЕ СКОРОСТИ РАСПРОСТРАНЕНИЯ ПРОДОЛЬНЫХ ЗВУКОВЫХ ВОЛН
Продольные звуковые волны в газах и металлах пред-ставляют собой периодические чередования сжатий и раз-режений в соответствующей среде. При этом перенос энер-гии осуществляется без переноса вещества, т.е. частицы среды не вовлекаются в поступательное движение среды, в которой распространяется звуковая волна, а совершают ко-лебания относительно своих положений равновесия. Вслед-ствие взаимодействия между частицами эти колебания рас-пространяются в среде с некоторой скоростью Уравнение бегущей волны, если фронт её можно полагать плоским, а распространение происходит вдоль оси
где
Решение уравнения (8.1) при распространении волны в безграничной среде описывается функцией:
где
В тех случаях, когда на пути бегущей волны встречается преграда, отраженная волна интерферирует с падающей и образуется стоячая волна. Если начало отсчета
Из уравнения (8.3) видно, что в каждой точке стоячей волны с координатой
В точках, координаты которых удовлетворяют условию:
где
Пучность представляет собой не точку, а плоскость, в которой совершаются колебания, описываемые соотноше-нием (8.3) при В точках, координаты которых удовлетворяют условию:
где
Узел, как и пучность, представляет собой не точку, а плос-кость, точки которой имеют координату Из соотношений (8.6) и (8.7) следует, что расстояние между соседними пучностями (или узлами) равно
Скорость перемещения частиц равна первой производной от соотношения (8.2) и также имеет свои пучности и узлы, совпадающие с узлами и пучностями смещения. При этом, ко-гда смещение и деформация, равная
достигают максимальных значений, скорость частиц обра-щается в нуль и наоборот. Соответственно, дважды за период происходит превра-щение энергии стоячей волны то полностью в кинетическую (пучность скорости), то полностью в потенциальную (пуч-ность деформации). В результате происходит переход энер-гии от каждого узла к соседним с ним пучностям и обратно. Средний по времени поток энергии в любом поперечном сечении стоячей волны равен 0. Хотя общий характер распространения продольных зву-ковых волн в металлах и газах одинаков, расчетные зна-чения их фазовых скоростей определяются по различным соотношениям, что обусловлено различиями в степени связи между частицами в различных средах. Скорость распростра-нения звуковых волн в газе:
где
Скорость распространения продольных звуковых волн в металлических стержнях равна:
где
Значения модуля Юнга и плотности для используемых в лабораторной работе материалов приведены в таблице 1.
Таблица 1
|

 , образуя бегущую волну.
, образуя бегущую волну. , имеет вид:
, имеет вид: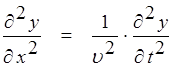 , (8.1)
, (8.1) – смещение колеблющихся частиц;
– смещение колеблющихся частиц; , (8.2)
, (8.2) – циклическая частота;
– циклическая частота; – частота колебаний;
– частота колебаний; – волновое число;
– волновое число; – период колебаний;
– период колебаний; – длина волны;
– длина волны; – текущее время;
– текущее время; – значение координаты вдоль оси
– значение координаты вдоль оси  ;
; – начальная фаза волны;
– начальная фаза волны; – амплитуда волны.
– амплитуда волны. (8.3)
(8.3) , что и у встречных волн. Ампли-туда указанных колебаний зависит от величины
, что и у встречных волн. Ампли-туда указанных колебаний зависит от величины  . (8.4)
. (8.4) (8.5)
(8.5) , амплитуда колебаний (по модулю) макси-мальна. Эти точки называются пучностями стоячей волны. Из соотношения (8.5) следует, что значения координат пуч-ностей равны:
, амплитуда колебаний (по модулю) макси-мальна. Эти точки называются пучностями стоячей волны. Из соотношения (8.5) следует, что значения координат пуч-ностей равны: . (8.6)
. (8.6) .
. , (8.7)
, (8.7) , амплитуда колебаний минимальна. Эти точ-ки называются узлами. Их координаты:
, амплитуда колебаний минимальна. Эти точ-ки называются узлами. Их координаты: . (8.8)
. (8.8) . Пуч-ности и узлы сдвинуты друг относительно друга на чет-верть длины волны. Указанные факты используются для экспериментального определения длины волны колебаний. Наиболее целесообразно, если не возникает каких-либо препятствий технического характера, определять длину волны путем измерения расстояния между пучностями. По известной частоте источника колебаний и измеренной дли-не волны определяется скорость распространения волн:
. Пуч-ности и узлы сдвинуты друг относительно друга на чет-верть длины волны. Указанные факты используются для экспериментального определения длины волны колебаний. Наиболее целесообразно, если не возникает каких-либо препятствий технического характера, определять длину волны путем измерения расстояния между пучностями. По известной частоте источника колебаний и измеренной дли-не волны определяется скорость распространения волн: . (8.9)
. (8.9) , (8.10)
, (8.10) , (8.11)
, (8.11) – постоянная адиабаты (для воздуха
– постоянная адиабаты (для воздуха  );
); Дж ·моль
Дж ·моль  К
К  – молярная масса газа (для воздуха
– молярная масса газа (для воздуха  кг·моль
кг·моль  , (8.12)
, (8.12) – модуль Юнга, Па;
– модуль Юнга, Па; – плотность материала стержня, кг·м
– плотность материала стержня, кг·м  ;
;


