Краткая теория. Как известно, электрическое сопротивление R провода длиной l и поперечным сечением S определяется формулой
Как известно, электрическое сопротивление R провода длиной l и поперечным сечением S определяется формулой
где r - удельное сопротивление материала (т.е. сопротивление проводника из данного материала поперечным сечением 1 м2 и длиной 1 м, измеряется в Омּм). Отсюда, при известных (измеренных) значениях R, l и d (d - диаметр проволоки) r можно определить как
В свою очередь, R может быть экспериментально определено из закона Ома для однородного участка цепи:
Здесь U - разность потенциалов на концах проводника, I - сила тока в нем. Формула (3) давала бы достаточно точный результат при условии идеальности измерительных приборов - амперметра и вольтметра, - а именно: сопротивление амперметра Метод вольтметра-амперметра для измерения сопротивления может быть реализован в двух вариантах: метод непосредственного измерения напряжения и метод непосредственного измерения тока. Рассмотрим особенности каждого из них.
1.1. На рис. 1 показана схема включения приборов для этого метода. Здесь RX – измеряемое неизвестное сопротивление исследуемого проводника, R1 – реостат для установки требуемого значения силы тока. При таком включении приборов амперметр показывает ток IA, равный сумме токов IX и IV текущих соответственно через сопротивление RX и вольтметр. Тогда сопротивление R’, вычисленное по формуле (3), будет отличаться от RX. Действительно, учитывая, что
Относительная систематическая погрешность
Отсюда видно, что при таком подключении измерительных приборов погрешность возникает из-за конечного сопротивления вольтметра RV. При RV ® ¥ εR ® 0. Для уменьшения погрешности важно, чтобы RX << RV, т.е. с помощью метода непосредственного измерения напряжения целесообразно измерять малые сопротивления. Если RV известно, то исключить систематическую погрешность можно, выразив RX из равенства (4):
где В используемой установке RV = 2000 Ом, а R’ < 5 Ом, таким образом, отношение R’/RV имеет порядок 10 – 3. В этом случае можно использовать приближение
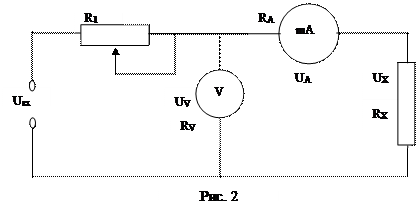
1.2. МЕТОД НЕПОСРЕДСТВЕННОГО ИЗМЕРЕНИЯ ТОКА Принципиальная схема включения измерительных приборов для этого метода представлена на рис. 2.
Здесь RX - измеряемое неизвестное сопротивление, а R1 – реостат для регулировки тока. При вычислении сопротивления из непосредственного измерения по формуле
возникает систематическая погрешность из-за того, что вольтметр показывает сумму падений напряжения на сопротивлениях RX и RA, т.е.
В этом случае
Относительная систематическая погрешность для этого варианта подключения амперметра и вольтметра определяется соотношением
откуда следует, что данный метод лучше использовать в случае, когда измеряемое сопротивление много больше сопротивления амперметра, т.е. RX >> RA. Если сопротивление RA известно, то исключить систематическую погрешность можно, выразив RX из равенства (10):
Тогда рабочая формула для расчета удельного сопротивления будет иметь вид:
|

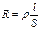 , (1)
, (1) . (2)
. (2)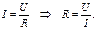 (3)
(3) ; сопротивление вольтметра
; сопротивление вольтметра  . Поскольку на практике RA и RV имеют определенные конечные значения, то результат определения R, и, следовательно, r зависит от схемы (способа) подключения приборов.
. Поскольку на практике RA и RV имеют определенные конечные значения, то результат определения R, и, следовательно, r зависит от схемы (способа) подключения приборов.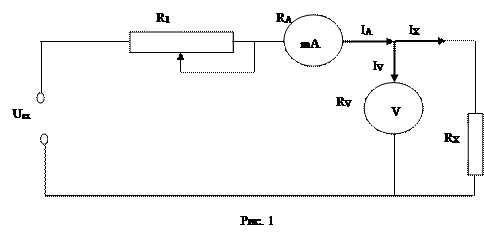
 ,
, 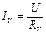 ,
, 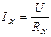 , можем записать:
, можем записать: (4)
(4) для этого варианта подключения амперметра и вольтметра определяется соотношением
для этого варианта подключения амперметра и вольтметра определяется соотношением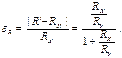 (5)
(5)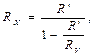 (6)
(6)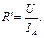
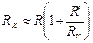 , и окончательно рабочая формула для расчета удельного сопротивления будет иметь вид:
, и окончательно рабочая формула для расчета удельного сопротивления будет иметь вид: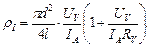 (7)
(7)
 (8)
(8)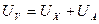 . (9)
. (9) . (10)
. (10)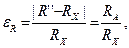 (11)
(11)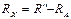 . (12)
. (12)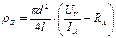 . (13)
. (13)


