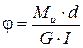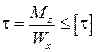V2: Продольная сила. Напряжения и деформации
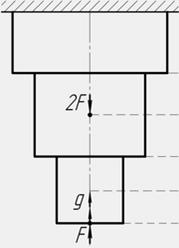
I: K=B S: Для стержня, схема которого изображена на рисунке,
нормальные напряжения, действующие в сечении 1-1, будут… -: растягивающими и сжимающими -: сжимающими -: равны нулю +: растягивающими
I: K=B S: Для стержня, схема которого изображена на рисунке,
нормальные напряжения, действующие в сечении 1-1, будут… -: растягивающими и сжимающими -: растягивающими -: равны нулю +: сжимающими
I: K=B S: Для стержня, схема которого изображена на рисунке,
деформации, возникающие в сечении 1-1, будут… -: сжимающими -: растягивающими и сжимающими +: растягивающими -: равны нулю
I: K=B S: Для стержня, схема которого изображена на рисунке,
деформации, возникающие в сечении 1-1, будут… -: сжимающими +: растягивающими -: растягивающими и сжимающими -: равны нулю
I: K=B S: Для стержня, схема которого изображена на рисунке,
деформации, возникающие в сечении 1-1, будут… -: сжимающими -: растягивающими и сжимающими +: растягивающими -: равны нулю
I: K=С S: Чему равны напряжения в сечении I-I если P1=20 кН, Р2=5кН, а площадь поперечного сечения равна 5×10-4 м2
-: 40 МПа; -: 10 МПа; +: 30 МПа; -: 50 МПа
I: K=С S: Ступенчатый брус нагружен силами
-: -: -: +:
I: K=A S: Условие прочности при растяжении-сжатии … -: +: -: -:
I: K=A S: В поперечных сечениях бруса при центральном растяжении или сжатии возникают равномерно распределенные напряжения, равные отношению продольной силы к площади поперечного сечения. Что это за напряжения? -: касательные -: равнодействующие +: нормальные -: суммарные
I: K=B S: Отношение относительной поперечной деформации к продольной, взятое по абсолютной величине называется +: коэффициентом Пуассона -: модулем упругости -: модулем Юнга -: коэффициентом скольжения
I: K=A S: Обозначение внутреннего силового фактора при растяжении-сжатии… -: +: -: -:
I: K=A S: Виды напряжений, возникающих при растяжении-сжатии… -: касательные +: нормальные -: касательные и нормальные -: деформированные
I: K=B S: Параметр -: Модуль сдвига +: Модуль упругости -: Модуль сопротивления -: Модуль инерции
I: K=A S: Условие прочности при растяжении-сжатии… -: +: -: -:
I: K=B S: Закон Гука при растяжении-сжатии… +: -: -: -:
I: K=B S: Укажите соответствующую нагружению стержня эпюру продольных сил в поперечных сечениях бруса(F – сосредоточенная нагрузка, q – распределенная нагрузка).
-: -: +: -:
I: K=B S: Укажите соответствующую нагружению стержня эпюру продольных сил в поперечных сечениях бруса(F – сосредоточенная нагрузка).
+: -: -: -:
I: K=B S: Укажите схему нагружения бруса соответствующую эпюре продольных сил (F – сосредоточенная нагрузка, q – распределенная нагрузка)....
+: -: -: -:
I: K=B S: Укажите соответствующую нагружению стержня эпюру продольных сил в поперечных сечениях бруса(F – сосредоточенная нагрузка, q – распределенная нагрузка).
+: -: -: -:
I: K=B S: Укажите соответствующую нагружению стержня эпюру продольных сил в поперечных сечениях бруса(q – распределенная нагрузка).
-: +: -: -:
I: K=B S: Для стержня, схема которого изображена на рисунке, нормальные напряжения, действующие в сечении 2-2, будут…
-: растягивающими и сжимающими -: растягивающими +: равны нулю -: сжимающими
I: K=B S: Для стержня, схема которого изображена на рисунке, нормальные напряжения, действующие в сечении 3-3, будут…
-: растягивающими и сжимающими +: растягивающими -: равны нулю -: сжимающими
I: K=B S: Для стержня, схема которого изображена на рисунке, нормальные напряжения, действующие в сечении 3-3, будут…
-: растягивающими и сжимающими -: растягивающими -: равны нулю +: сжимающими
I: K=B S: Для стержня, схема которого изображена на рисунке, нормальные напряжения, действующие в сечении 3-3, будут…
-: растягивающими и сжимающими +: растягивающими -: равны нулю -: сжимающими
I: K=B S: Для стержня, схема которого изображена на рисунке, нормальные напряжения, действующие в сечении 2-2, будут…
-: растягивающими и сжимающими +: растягивающими -: равны нулю -: сжимающими
I: K=B S: Для стержня, схема которого изображена на рисунке, нормальные напряжения, действующие в сечении 1-1, будут…
-: растягивающими и сжимающими +: растягивающими -: равны нулю -: сжимающими
I: K=B S: Для стержня, схема которого изображена на рисунке, нормальные напряжения, действующие в сечении 1-1, будут…
-: растягивающими и сжимающими +: растягивающими -: равны нулю -: сжимающими
I: K=B S: Для стержня, схема которого изображена на рисунке, нормальные напряжения, действующие в сечении 2-2, будут…
-: растягивающими и сжимающими +: растягивающими -: равны нулю -: сжимающими
I: K=B S: Для стержня, схема которого изображена на рисунке, нормальные напряжения, действующие в сечении 3-3, будут…
-: растягивающими и сжимающими +: растягивающими -: равны нулю -: сжимающими
I: K=B S: Для стержня, схема которого изображена на рисунке, нормальные напряжения, действующие в сечении 3-3, будут…
-: растягивающими и сжимающими -: растягивающими -: равны нулю +: сжимающими
I: K=B S: Для стержня, схема которого изображена на рисунке, нормальные напряжения, действующие в сечении 2-2, будут…
-: растягивающими и сжимающими -: растягивающими -: равны нулю +: сжимающими
I: K=B S: Для стержня, схема которого изображена на рисунке, нормальные напряжения, действующие в сечении 1-1, будут…
-: растягивающими и сжимающими -: растягивающими -: равны нулю +: сжимающими
|

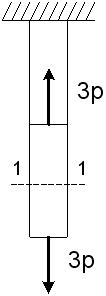


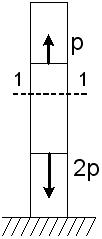

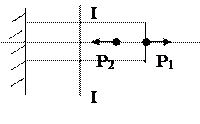
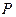 и
и  , а левого
, а левого  . Если
. Если 
 ;
; ;
;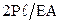 ;
;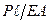 ;
; ;
; ;
;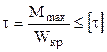 ;
;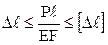 .
.

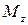
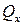
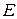 в формуле деформации
в формуле деформации  …
…