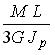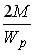V2: Крутящий момент. Деформации и напряжения

 

I: K=A

S: Крутящим моментом называется…

-: равнодействующий момент касательных и нормальных напряжений;

-: равнодействующий момент нормальных напряжений;

+: равнодействующий момент касательных напряжений;

-: равнодействующий момент продольных сил относительно оси стержня.

 

I: K=B

S: В процессе скручивания стержня диагональ (cb )…

-: искривляется;

- размер и форма диагонали не изменяются;

-: укорачивается;

+: удлиняется.

 

I: K=B

S: Если к тонкостенной трубе приложен скручивающий момент M, то напряженным состоянием для элементарного объема «abcd » будет…

-: сложное напряженное состояние;

+: чистый сдвиг;

-: объемное напряженное состояние;

-: линейное напряженное состояние.

 

I: K=A

S: При скручивании стержня круглого поперечного сечения главные площадки в точке, расположенной вблизи поверхности, совпадают…

-: с продольными сечениями стержня;

-: с продольными и поперечными сечениями стержня;

-: с поперечными сечениями стержня;

+: с внешней поверхностью и двумя сечениями под углом к продольной оси стержня.

 

I: K=B

S: В сечении 1–1 крутящий момент по модулю равен…

-:

-:

+:

-:

 

I: K=C

S: Угол поворота сечения С равен…

-:

-:

+:

-:

 

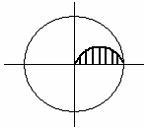
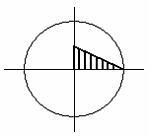
I: K=B

S: Изменение касательных напряжений вдоль радиуса поперечного сечения круглого стержня при кручении соответствует рисунку…

-:

+:

-:

-:

 

I: K=B

S: Касательное напряжение в центре тяжести поперечного сечения (точка K) равно…

+: 0

-:

-:

-:

 

I: K=A

S: Видом напряженного состояния, имеющего место при кручении стержня круглого поперечного сечения, является…

-: одноосное напряженное состояние

-: линейное напряженное состояние

+: чистый сдвиг

-: объемное напряженное состояние

 

I: K=A

S: Эпюра крутящего момента имеет вид…

-: 4

-: 3

+: 1

-: 2