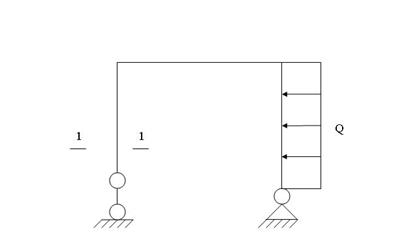
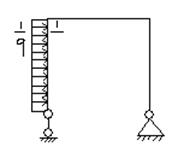
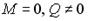V2: Поперечная сила и изгибающий момент и их эпюры

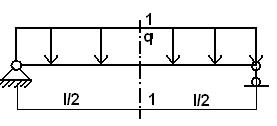
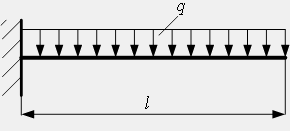
I: K=A

S: В сечении 1-1 имеют место внутренние силовые факторы …

-:

+:

-:

-:

I: K=B

S: В сечении 1-1 имеют место внутренние силовые факторы …

-:

+:

-:

-:

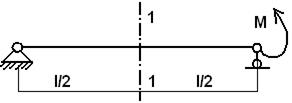
I: K=B

S: В сечении 1-1 имеют место внутренние силовые факторы …

-:

-:

-:

+:

I: K=B

S: В сечении 1-1 имеют место внутренние силовые факторы …

-:

-:

-:

+:

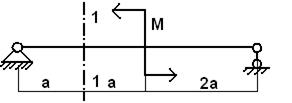
I: K=B

S: В сечении 1-1 имеют место силовые факторы:

+: ;

-: ;

-: ;

-: .

I: K=A

S: В сечении 1-1 имеют место силовые факторы:

+: ;

-: ;

-: ;

-: .

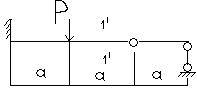
I: K=A

S: В сечении 1-1 имеют место силовые факторы…

+: M=0, Q≠0

-: M=0, Q=0

-: M≠0, Q≠0

-: M≠0, Q=0

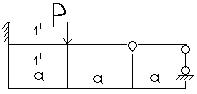
I: K=D

S: В сечении 1-1 имеют место силовые факторы…

+: M=0, Q=0

-: M≠0, Q≠0

-: M≠0, Q=0

-: M=0, Q≠0

I: K=B

S: В сечении 1-1 имеют место силовые факторы…

+: M=0, Q=0

-: M≠0, Q≠0

-: M≠0, Q=0

-: M=0, Q≠0

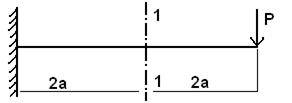
I: K=A

S: В сечении 1-1 имеют место силовые факторы…

+: M≠0, Q≠0

-: M≠0, Q=0

-: M=0, Q=0

-: M=0, Q≠0

I: K=C

S: В сечении 1-1 имеют место силовые факторы:

+: M=0, Q=0

-: M=0, Q≠0

-: M≠0, Q=0

-: M≠0, Q≠0

I: K=A

S: На тех участках балки, где распределенная нагрузка отсутствует:

+: поперечные силы постоянны, а изгибающие моменты меняются по линейному закону

-: поперечные силы равны 0

-: изгибающие моменты равны 0

-: эпюра изгибающих моментов изображается кривой линией

I: K=A

S: На тех участках балки, где действует распределенная нагрузка:

+: поперечные силы изменяются по длине балки: эпюры изгибающих моментов ограничены кривыми

-: изгибающие моменты изменяются по линейному закону

-: поперечные силы неизменны

-: изгибающие моменты неизменны

I: K=B

S: На тех участках балки, где поперечная сила имеет постоянное значение:

+: эпюра изгибающих моментов ограничена прямой линией

-: эпюра изгибающих моментов постоянна

-: эпюра изгибающих моментов носит убывающий характер

-: эпюра изгибающих моментов носит возрастающий характер

I: K=B

S: Для балки, снабженной шарниром, в шарнире

+: изгибающий момент равен 0

-: поперечная сила равна 0

-: изгибающий момент принимает экстремальное значение

-: поперечная сила минимальна

I: K=C

S: Любой скачок на эпюре изгибающих моментов равен:

+: сосредоточенному моменту, приложенному в этом сечении

-: поперечной силе, приложенной в этом сечении

-: сумме всех изгибающих моментов, приложенных к контуру

-: внешнему сосредоточенному моменту

I: K=C

S: Любой скачок на эпюре поперечных сил равен:

+: сосредоточенной силе, приложенной в этом сечении

-: сосредоточенному моменту, приложенному в этом сечении

-: сумме всех изгибающих моментов, приложенных к конструкции

-: сумме всех поперечных сил, приложенных к конструкции

I: K=A

S: На тех участках балки, где поперечные силы положительны…

+: изгибающий момент возрастает

-: изгибающий момент убывает

-: действует распределенный момент

-: изгибающий момент имеет постоянное значение

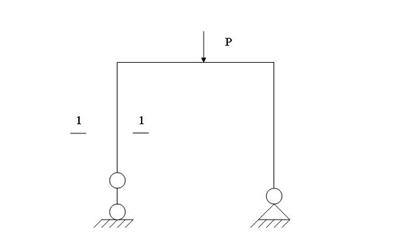
I: K=C

S: Статически неопределенная система изображена на рисунке…

+:

-:

-:

-:

I: K=A

S: Степень статической неопределенности рамы, изображенной на рисунке равна…

+: 1

-: 2

-: 3

-: 4

I: K=B

S: В сечении 1-1 имеют место внутренние силовые факторы…

-:

-:

-:

+:

I: K=В

S: В сечении 1-1 имеют место внутренние силовые факторы…

+:

-:

-:

-:

I: K=A

S: В сечении 1-1 имеют место внутренние силовые факторы…

-:

-:

-:

+:

I: K=B

S: В сечении 1-1 имеют место силовые факторы…

+: M≠0,Q≠0

-: M=0,Q≠0

-: M=0,Q=0

-: M≠0,Q=0

I: K=A

S: В сечении 1-1 имеют место силовые факторы…

+: M≠0,Q≠0

-: M=0,Q≠0

-: M=0,Q=0

-: M≠0,Q=0

I: K=B

S: В сечении 1-1 имеют место силовые факторы…

-: M≠0,Q≠0

-: M=0,Q≠0

-: M=0,Q=0

+: M≠0,Q=0

I: K=C

S: В сечении 1-1 имеют место силовые факторы…

+: M≠0,Q=0

-: M=0,Q≠0

-: M≠0,Q≠0

-: M=0,Q=0

I: K=C

S: В сечении 1-1 имеют место силовые факторы…

+: M≠0,Q≠0

-: M=0,Q≠0

-: M=0,Q=0

-: M≠0,Q=0

I: K=A

S: В сечении 1-1 имеют место силовые факторы…

+: M≠0,Q≠0

-: M=0,Q≠0

-: M=0,Q=0

-: M≠0,Q=0

I: K=A

S: В сечении 1-1 имеют место силовые факторы…

+: M≠0,Q≠0

-: M=0,Q≠0

-: M=0,Q=0

-: M≠0,Q=0

I: K=B

S: В сечении 1-1 имеют место силовые факторы…

+: M≠0,Q≠0

-: M=0,Q≠0

-: M=0,Q=0

-: M≠0,Q=0

I: K=B

S: Укажите эпюру поперечной силы в сечениях консольной балки…

-:

+:

-:

-:

I: K=B

S: Укажите эпюру изгибающего момента в сечениях консольной балки…

+:

-:

-:

-:

I: K=B

S: Эпюра поперечной силы в сечениях консольной балки…

+:

-:

-:

-:

I: K=B

S: Эпюра изгибающего момента в сечениях консольной балки…

-:

-:

+:

-:

I: K=B

S: N – продольная сила, Q_y – поперечная сила, M_x – изгибающий момент

В плоских рамах возникают:

+: силовые факторы N, Q_y, M_x

-: силовые факторы N, Q_y

-: силовые факторы Q_y, M_x

-: силовые факторы N, M_x

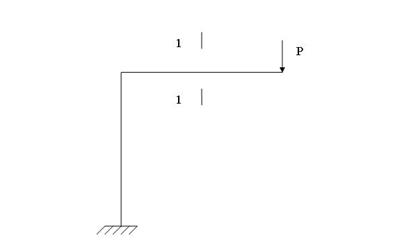
I: K=A

S: В сечении 1-1 имеют место силовые факторы:

+:N=0, Q≠0, M≠0

-: N≠0, Q≠0, M≠0

-: N=0, Q=0, M=0

-: N≠0, Q=0, M=0

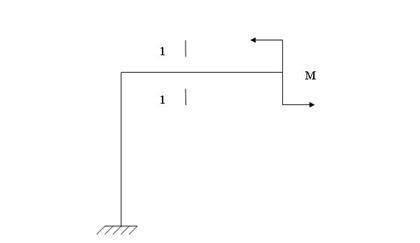
I: K=A

S: В сечении 1-1 имеют место силовые факторы:

+: N=0, Q=0, M≠0

-: N=0, Q≠0, M=0

-: N≠0, Q≠0, M≠0

-: N=0, Q≠0, M≠0

I: K=C

S: В сечении 1-1имеют место силовые факторы:

+: N=0, Q=0, M≠0

-: N=0, Q≠0, M=0

-: N≠0, Q=0, M≠0

-: N≠0, Q≠0, M≠0

I: K= B

S: В сечении 1-1 имеют место силовые факторы:

+: N≠0, Q=0, M≠0

-: N=0, Q≠0, M≠0

-: N≠0, Q=0, M=0

-: N=0, Q=0, M≠0

I: K= B

S: В сечении 1-1 имеют место силовые факторы:

+: N=0, Q≠0, M≠0

-: N=0, Q=0, M≠0

-: N≠0, Q=0, M≠0

-: N≠0, Q≠0, M≠0

I: K= B

S: В сечении 1-1 имеют место силовые факторы:

+: N≠0, Q=0, M=0

-: N<>0, Q≠0, M=0

-: N=0, Q≠0, M≠0

-: N=0, Q=0, M≠0

I: K= B

S: В сечении 1-1 имеют место силовые факторы:

+: N≠0, Q=0, M=0

-: N≠0, Q≠0, M=0

-: N=0, Q=0, M≠0

-: N=0, Q≠0, M≠0

I: K=C

S: В сечении 1-1 имеют место силовые факторы:

+: N≠0, Q=0, M=0

-: N≠0, Q≠0, M=0

-: N=0, Q=0, M≠0

-: N=0, Q≠0, M=0

I: K=C

S: в сечении 1-1 имеют место силовые факторы

+: N≠0, Q≠0, M≠0

-: N≠0, Q=0, M=0

-: N=0, Q=0, M≠0

-: N=0, Q≠0, M≠0

I: K= B

S: в сечении 1-1 имеют место силовые факторы

+: N=0, Q=0, M=0

-: N=0, Q≠0, M≠0

-: N≠0, Q≠0, M≠0

-: N≠0, Q=0, M=0

I: K=A

S: в сечении 1-1 имеют место силовые факторы

+: N=0, Q=0, M=0

-: N=0, Q≠0, M≠0

-: N≠0, Q=0, M=0

-: N≠0, Q≠0, M≠0

I: K= B

S: в сечении 1-1 имеют место силовые факторы

+: N=0, Q=0, M=0

-: N=0, Q≠0, M≠0

-: N≠0, Q=0, M=0

-: N≠0, Q≠0, M≠0

I: K=C

S: в сечении 1-1 имеют место силовые факторы

+: N≠0, Q=0, M=0

-: N≠0, Q≠0, M=0

-: N=0, Q=0, M≠0

-: N=0, Q≠0, M≠0

I: K= B

S: в сечении 1-1 имеют место силовые факторы

+: N≠0, Q=0, M=0

-: N≠0, Q≠0, M=0

-: N=0, Q=0, M≠0

-: N=0, Q≠0, M≠0
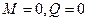
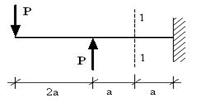