V2: Деформируемое состояние в точке. Связь между деформациями и напряжениями
I: K=В S: Компоненты тензора деформаций +: деформированное состояние в точке -: напряженное состояние тела -: напряженное состояние в точке -: деформированное состояние тела
I: K=С S: По трем граням элементарного параллелепипеда действуют нормальные напряжения
-: I, II -: все ребра деформируются одинаково +: II, III -: I, III
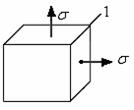
I: K=С S: По двум граням элементарного параллелепипеда действуют нормальные напряжения
+: I, II -: I, III -: II, III -: I, II, III
I: K=В S: Относительная линейная деформация -: +: -: -:
I: K=A S: Эпюра касательных напряжений в сечении I – I имеет вид…
+: -: -: -:
I: K=В S: Правильные направления нормальных напряжений в точках 1, 2 сечения С-С имеют вид…
-: +: -: -:
I: K=В S: Если правую часть стержня отбросить, то в точке 1 сечения С-С следует показать напряжения…
+: -: -: -:
I: K=В S: При отбрасывании левой части стержня, в точке 1 сечения С-С будут действовать напряжения…
-: +: -: -:
I: K=В S: Относительные линейные деформации e1,e2,e3 (e1=emax, e3= emin) называются … +: главными деформациями -: максимальными деформациями -: экстремальными деформациями -: предельными деформациями
|
, 
, 
, 
, 
, 
, представленные в виде функций координат X, Y, Z, определяют…
. Одинаковую деформацию 
имеют ребра…
. Одинаковую по модулю деформацию 
