Снежинка Кох
Снежинка Коха, отличающейся от кривой его же имени лишь тем, что строится на основе равностороннего треугольника, в результате чего получается бесконечная прямая, покрывающая ограниченную плоскость. Результаты показали, что снежинка Кох самоподобна, имеет дробную размерность, большую ее топологической размерности. Таким образом, при n стремящемся к бесконечности снежинка Кох становится фрактальным объектом. При неограниченном увеличении числа звеньев длина ломанных в пределе стремится к бесконечности, хотя площадь заключённого внутри ломанных участка плоскости остаётся конечной. Ещё два маленьких замечания: к предельной кривой ни в одной точке нельзя провести касательную, а площадь снежинки стремится к 8/5 от площади исходного треугольника. Это фигура бесконечной длины, но бесконечная кривая покрывает ограниченную площадь.
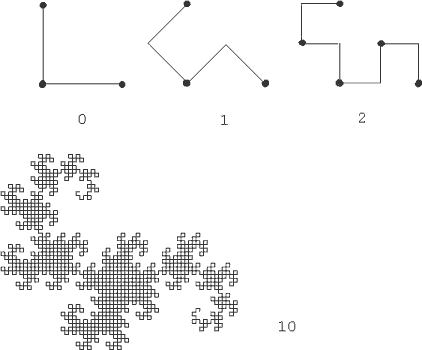
Алгоритм построения фрактала o Задаем начальные условия: нулевое поколение представляет собой правильный треугольник S0 со стороной 1. o Задаем процедуру, которая преобразует нулевое поколение: делим средними линиями исходный правильный треугольник на четыре равных треугольника и центральный выбрасываем. Получаем множество S1, состоящее из трёх треугольников со стороной 1/2. o С тремя оставшимися делаем то же самое и так до бесконечности. В результате возникнет убывающая последовательность замкнутых множеств Sn, и салфетка S есть их пересечение. Множество Sn состоит из 3n правильных треугольников, стороны которых имеют длину 1/2n и принадлежат S по построению Салфетка содержит бесконечную сетку - каркас, образованный сторонами всех участвующих в построении треугольников. Салфетка самоподобна - она состоит из кусков, каждый из которых подобен целому с коэффициентом подобия 1/2. "Выколем" точки, в которых эти куски соединяются, - середины сторон исходного треугольника. Тогда салфетка распадётся на три салфетки меньшего размера. С ними проделаем то же самое. Что станет с салфеткой, если этот процесс продолжить до бесконечности, выколов лишь счётное множество точек? Салфетка полностью рассыплется! Итак, взяв любой из образовавшихся треугольников и увеличив его - получим точную копию целого, т.е множество самоподобно. Вывод Результаты показали, что салфетка Серпинского самоподобна, имеет дробную размерность, меньшую ее топологической размерности. Таким образом, при n стремящемся к бесконечности салфетка Серпинского становится фрактальным объектом. «Дракон» Драконова ломаная относится к классу самоподобных рекурсивно порождаемых геометрических структур. Ломаная нулевого порядка представляет собой просто прямой угол. Изображение фигуры каждого следующего порядка строится путем рекурсивных замен каждого из отрезков фигуры младшего порядка на два отрезка, сложенных также в виде прямого угла. При этом каждый первый угол оказывается "вывернутым" наружу, а каждый второй - вовнутрь. На рисунке проиллюстрирован алгоритм построения драконовой ломаной и изображен вполне взрослый "дракон" десятого порядка.
|

 3. Салфетка Серпинского
3. Салфетка Серпинского