Триадная кривая КохКривая была открыта Гельге фон Кох в 1904 году. Алгоритм построения фрактала: Задаем начальные условия: берем отрезок единичной длины: это нулевое поколение кривой Кох. Задаем генератор: это ломаная кривая, состоящая из четырех элементарных отрезков длины r = 1/3. Получим первое поколение: отрезок единичной длины делим на три части. Среднюю часть отбрасываем и заменяем на ломаную-генератор в соответствующем масштабе. Поскольку на каждом шаге отрезок разбивается на три части, множество называется триадной кривой Кох. Получим второе поколение: каждое из четырех звеньев делим на три части, среднюю часть выбрасываем и заменяем на генератор. Итак, для получения каждого последующего поколения, все звенья предыдущего поколения необходимо заменить уменьшенным образующим элементом. Вам были представлены четыре поколений кривой. При n стремящемся к бесконечности кривая Кох становится фрактальным обьектом. Легко видеть, что размерность Хаусдорфа данного фрактального образования определяется соотношением: Результаты показали, что триадная кривая Кох самоподобна, имеет дробную размерность, большую ее топологической размерности. Таким образом, при n стремящемся к бесконечности кривая Кох становится фрактальным объектом. Фрактал представляет изощренную ломаную линию: она уже не линия, но еще и не плоскость. Фрактальная размерность, показывает насколько плотно линия заполняет плоскость, т.е. характеризует степень скрученности, извилистости линии. [1 ведущий]
|
(
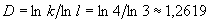- число элементов,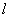 
- относительный размер элементов).
