Двойственные задачи линейного программирования.
Любую задачу максимизации с экономической точки зрения можно рассматривать как задачу о распределении ограниченных ресурсов b1, b2,…, bn между различными потребителями, например, между некоторыми технологическими процессами, которые представляются столбцами A1, А2,..., Аm матрицы ограничений задачи. Любое допустимое решение задачи линейного программирования х1, х2,..., хm дает конкретное распределение, указывающее ту долю каждого из ресурсов, которая должна быть использована при осуществлении соответствующего технологического процесса. Рассмотрим пример. Завод производит три вида продукции х1, x2 и x3, каждый из которых требует затрат времени на обработку на токарном, фрезерном и сверлильном станках. Количество машинного времени для каждого из станков ограничено. Пусть с1, c2 и c3 — прибыль от реализации единицы соответствующего вида продукции. Необходимо определить, какое количество каждого вида продукции необходимо производить в течение недели, чтобы получить максимальную прибыль. Формально эта задача записывается так: найти при ограничениях
где a1j, a2j, a3j — время, необходимое для обработки единицы j-го вида продукции соответственно на токарном, фрезерном и сверлильном станках (j = 1, 2, 3); b1, b2, b3 — недельный ресурс машинного времени соответственно для токарного, фрезерного и сверлильного станков. Обозначим y1, y2 и y3 — цену единицы времени работы на токарном, фрезерном и сверлильном станках. Тогда a1jy1 + a2jy2+ a3jy3 можно трактовать как расходы на изготовление единицы продукции вида j. Предположим, что цены ресурсов y1, y2 и y3 выбраны так, что выполняются следующие соотношения:
Поскольку b1, b2, b3 — использованный ресурс машинного времени для каждого из станков, то b1y1 + b2y2 + b3y3 — суммарные расходы на производство. Требуется найти такие y1, y2 и y3, удовлетворяющие условиям (3), при которых минимизируются суммарные расходы на производство: min g(y1, y2, y3)= b1y1 + b2y2 + b3y3, (4) y1³ 0, y2³ 0, y3³ 0. Такую задачу называют двойственной задачей по отношению к задаче (1), называемой прямой. Запишем теперь прямую и двойственную задачи в общем случае. Прямая задача
при условиях
Двойственная задача
при условиях
Сопоставляя формы записи прямой и двойственной задач, можно установить между ними следующие взаимосвязи: 1) если прямая задача является задачей максимизации, то двойственная будет задачей минимизации, и наоборот; 2) коэффициенты целевой функции прямой задачи c1, c2, …, cn становятся свободными членами ограничений двойственной задачи; 3) свободные члены ограничений прямой задачи b1, b2, …, bm становятся коэффициентами целевой функции двойственной задачи; 4) матрицу ограничений двойственной задачи получают транспонированием матрицы ограничений прямой задачи; 5) если знаки всех неравенств»,£в ограничениях прямой «то в двойственной задаче все ограничения»;³будут иметь знак « 6) число ограничений прямой задачи равно числу переменных двойственной задачи, а число ограничений двойственной задачи равно числу переменных прямой задачи. Переменные y1, y2,…, ym двойственной задачи иногда называют «теневыми ценами». Двойственную задачу выгоднее решать, чем исходную прямую, если в прямой задаче при малом количестве переменных имеется большое количество ограничений (т > n). Связь между оптимальными решениями прямой и двойственной задач устанавливают посредством следующих теорем теории двойственности. Теорема. Если x0 и у0 — допустимые решения прямой и двойственной задач, т. е. если £Ах0 b и АTy0 ³ с, то cTx0£ bTy0, т. е. значения целевой функции прямой задачи никогда не превышают значений целевой функции двойственной задачи.
|

 (1)
(1) (2)
(2) (3)
(3) (5)
(5) (6)
(6) . (7)
. (7)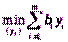 (8)
(8) (9)
(9) . (10)
. (10)


