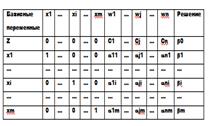
Целочисленные задачи линейного программирования. Постановка, примеры.Целочисленное программирование ориентировано на решение задач математического программирования, в которых все или некоторые переменные должны принимать только целочисленные значения. Задача называется полностью целочисленной, если условие целочисленности наложено на все переменные; когда это условие относится лишь к некоторым переменным, задача называется частично целочисленной. Если при этом целевая функция и функции, входящие в ограничения, линейные, то задача является задачей линейного программирования. Методы решения задач целочисленного программирования можно классифицировать как методы отсечений (1) и комбинаторные методы (2). Исходной задачей для методов отсечений, используемых при решении линейных целочисленных задач, является задача с ослабленными ограничениями, которая возникает в результате исключения требования целочисленности переменных. По мере введения специальных дополнительных ограничений, учитывающих требования целочисленности, многогранник допустимых решений ослабленной задачи постепенно деформируется до тех пор, пока координаты допустимого решения не станут целочисленными. Название «методы отсечений» связано с тем обстоятельством, что вводимые дополнительные ограничения отсекают (исключают) некоторые области многогранника допустимых решений, в которых отсутствуют точки с целочисленными координатами, В основе комбинаторных методов лежит идея перебора всех допустимых целочисленных решений, разумеется, на первый план здесь выдвигается проблема разработки тестовых процедур, позволяющих непосредственно рассматривать лишь относительно небольшую часть указанных решений, а остальные допустимые решения учитывать некоторым косвенным образом. Наиболее известным комбинаторным методом является метод ветвей и границ, который также опирается на процедуру решения задач с ослабленными ограничениями. При таком подходе из рассматриваемой задачи получаются две подзадачи путем специального «разбиения» пространства допустимых решений и отбрасывания областей, не содержащих допустимых целочисленных решений. В случае, когда целочисленные переменные являются булевыми, применяются комбинированные методы. Булевы свойства переменных существенно упрощают поиск решения. Алгоритм метода отсечений для решения полностью целочисленной задачи. Необходимым условием применения данного алгоритма является целочисленность всех коэффициентов и правых частей ограничений исходной задачи. Любое ограничение с рациональными коэффициентами легко приводится к требуемому виду путем умножения ограничения на наименьший общий знаменатель входящих в него коэффициентов. Алгоритм состоит в следующем. На первом шаге решается задача с ослабленными ограничениями, не содержащая условий целочисленности переменных. Если полученное оптимальное решение оказывается целочисленным, то оно является также решением исходной задачи. В противном случае следует ввести дополнительные ограничения, порождающие (вместе с некоторыми ограничениями) новую задачу линейного программирования, решение которой оказывается целочисленным и совпадает с оптимальным решением исходной целочисленной задачи. Пусть последняя симплекс-таблица задачи с ослабленными ограничениями имеет следующий вид:
Рассмотрим i-ую строку, которой соответствует нецелое значение базисной переменной xi, и выразим xi через небазисные переменные:
Каждую строку симплекс-таблицы, порождающую аналогичное равенство будем называть производящей строкой. Так как коэффициенты целевой функции можно считать целыми числами, переменная Z также должна быть целочисленной, и верхняя строка таблицы также может быть выбрана в качестве производящей. Пусть bI=[bI]+fi, aji=[aji]+fij, 0<fi<1, 0£fij<1. В качестве дополнительного ограничения вводим такое
|
, bI – нецелое.
,где Si – неотрицательная дополнительная переменная, которая по определению должна принимать целые значения. Такое ограничение равенство определяет отсечение Гомори для полностью целочисленной задачи. Добавив построенное ограничение в симплекс-таблицу, получим недопустимое, но оптимальное решение. В такой ситуации следует использовать двойственный симплекс-метод для получения допустимого и оптимального решения.
