Практическое занятие 5 - 6
На мою думку мета уроку була досягнута, діти активно працювали на уроці, були досягнуті всі етапи уроку. Урок пройшов емоційно, насичений великою кількістю нового матеріалу. Знання учнями були засвоєні на високому рівні.
Педагогічна задача №1 Підліток вилетів із-за рогу раптово і ледве не збив з ніг директора школи, який йшов назустріч. Винуватого залишили після уроків, вчинили рознос. У повітрі лунали залякуючі слова: неподобство, хуліганство….. «Якщо ти не розумієш цього, тоді підемо в міліцію,» - сказав нарешті класний керівник. - «там тобі пояснять що до цього». Чи правильно вчинили директор і класний керівник? Розв’язок 1. Хлопчик ледве не збив директора. Його залишили після уроків і почали залякувати. 2. а) Підліток, який порушив поведінку. б) Директор в) Класний керівник 3. Проблема в невмінні вихователів виявляти глибинні рушійні сили того чи іншого процесу: - не навчили їх - малий стаж роботи - авторитарний стиль керівництва В будь якому випадку не потрібно було залякувати учня, на мою думку потрібно було провести бесіду, пояснити, і на протязі певного часу поспостерігати за поведінкою учня, якщо потрібно зробити зауваження, поступово корегуючи поведінку учня.
Педагогічна задача №2 Учень постійно приходить на уроки не підготовленим, отримує негативні оцінки. Класний керівник зателефонував батькам учня і повідомив, що їхня дитина не готується до уроків. Батьки почувши це покарали свою дочку. Чи правильно поступили в цій ситуації батьки і класний керівник і чи потрібно карати дітей? Розв’язок 1. Учениця не готується до уроків. Про це було повідомлено її батькам. 2. а) Учениця б) Класний керівник в) Батьки дівчинки 3. Учень – 9 клас, 14 років Класний керівник 43 роки Батьки – молоді 34 роки 4. Проблема покаранні чи не каранні дитини і як мотивувати активну діяльність учня? 5. Можливо потрібно стимулювати діяльність дитини, дати стимул, чим повинні займатися як батьки так і вчителі, а не за кожну двійку наказувати дитину. Класний керівник хоче залучати і батьків до контролю навчання їхньої дитини, і сам контролює навчання дітей свого класу.
Педагогічна задача №3 На уроці історії між учнем і вчителем, розглядаючи спірне питання, виник спір, в розпалі якого вчитель образив учня. Учень в свою чергу розповів про цей інцидент батькам, а ті директору школи і наполягали щоб він розібрався в цій ситуації. Чи правильно поступив вчитель, учень, батьки, і що в цій ситуації робити директору школи? Розв’язок 1. Проблема не компетентного спілкування вчителя в суперечці з учнем. 2. а) Учень б) Вчитель в) Директор школи г) Батьки учня 3. Учень – 9 клас, 14 років. Вчитель історії 38 - років Директор школи – 55 років 4. Розбираючись в проблемі можна зробити висновок, що вчитель поступив не правильно по відношенню до учня. Учень в свою чергу повідомивши про це батькам, а вони директору школи, не залишив цю проблему не вирішеною. На мою думку директор розібравшись в ці ситуації і проаналізувавши її висунув вчителеві догану, поступив вірно. А вчитель у спілкуванні з дітьми повинен контролювати свої емоції. 8.125. 8.126. 8.127. 8.128. 8.130. 8.132. 8.133. 8.135. 8.136. 8.138. Степенным рядом называется функциональный ряд вида Радиусом сходимости степенного ряда Областью сходимости степенного ряда является интервал сходимости Интервал сходимости В задачах 8.140-8.160 найти область сходимости следующих степенных рядов: 8.140. 8.141. 8.142. 8.143. 8.144. 8.145. 8.146. 8.147. 8.148. 8.149. 8.150. 8.151. 8.154. 8.155. 8.156. 8.160. Внутри общего интервала сходимости Внутри интервала сходимости 1) Степенной ряд Представление функции При разложении функций в степенные ряды, как правило, используют основные разложения элементарных функций в ряд Маклорена: 1. 4., 5., 6., 7., 8.,,. Иногда при разложении используют почленное дифференцирование или интегрирование. При разложении в степенные ряды рациональных дробей рекомендуется представлять их в виде суммы простейших дробей. В задачах 8.161-8.178 используя основные разложения элементарных функций, а также возможность почленного дифференцирования и интегрирования степенных рядов, разложить функции в ряд Маклорена и указать интервалы сходимости полученных рядов. 8.161. 8.162. 8.163. 8.164. 8.166. 8.167. 8.168. 8.169. 8.170. 8.173. 8.175. 8.176. В задачах 8.179-8.186 вычислить указанные выражения с точностью 8.179. 8.180. 8.181. 8.182. 8.183. 8.184. 8.185. 8.186. В задачах 8.188-8.193 вычислить следующие интегралы с точностью 8.188. 8.189. 8.190. 8.191. 8.192. ОТВЕТЫ: 8.125 Практическое занятие 5 - 6 Тема: Современная образовательная система специальной педагогики
|

 , где
, где  - действительные числа. Числа
- действительные числа. Числа  называются коэффициентами ряда. Всякий степенной ряд сходится в точке
называются коэффициентами ряда. Всякий степенной ряд сходится в точке  .
. называется число
называется число  такое, что при
такое, что при  ряд сходится (и притом абсолютно), а при
ряд сходится (и притом абсолютно), а при  расходится. Интервал
расходится. Интервал  при этом называется интервалом сходимости ряда. На концах интервала сходимости, т.е. в точках
при этом называется интервалом сходимости ряда. На концах интервала сходимости, т.е. в точках  , ряд может как сходится, так и расходится.
, ряд может как сходится, так и расходится. , если в них ряд сходится. В частности, радиус сходимости
, если в них ряд сходится. В частности, радиус сходимости  , тогда область сходимости ряда состоит из одной точки
, тогда область сходимости ряда состоит из одной точки  , и
, и  , тогда областью сходимости ряда является вся числовая прямая.
, тогда областью сходимости ряда является вся числовая прямая. или
или 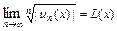 и решая неравенство
и решая неравенство 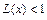 .
. .
. ; 2)
; 2)  .
. называется рядом Тейлора функции
называется рядом Тейлора функции  в точке
в точке  ряд Тейлора называется рядом Маклорена:
ряд Тейлора называется рядом Маклорена: 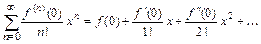 .
. , называется разложением
, называется разложением  ,
,  2.
2.  ,
,  ,
,  .
. .
. 8.126
8.126  8.127 Расходится. 8.128
8.127 Расходится. 8.128  8.130
8.130 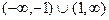 8.132
8.132  8.133
8.133  8.136
8.136 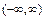 8.138
8.138  8.140
8.140  8.141
8.141 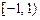 8.142
8.142  8.144
8.144  8.145
8.145  8.146
8.146  8.147
8.147  8.148
8.148  8.149
8.149  8.151
8.151  8.154
8.154  8.155
8.155  8.156
8.156  8.160
8.160  8.161
8.161  8.162
8.162  8.163
8.163 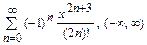 8.164
8.164  8.166
8.166  8.167
8.167  8.168
8.168  8.169
8.169  8.170
8.170  8.173
8.173  8.175
8.175 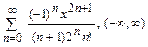 8.176
8.176  8.179
8.179  8.180
8.180  8.181
8.181  8.182
8.182  8.183
8.183  8.184
8.184 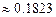 8.185
8.185  8.186
8.186 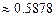 8.188
8.188 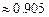 8.189
8.189  8.190
8.190  8.191
8.191 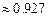 8.192
8.192 



