Программирование ветвлений с составными условиями
Составное – условие одновременной проверки нескольких операций отношения (логических величин). В математике запись составных условий осуществляется символами:
Например, условием нахождения точки с координатами x, y в 1-м квадранте будет: x>0 Символ «отрицание» позволяет расширить возможности формулировки логических условий. Так, запись Если один из операндов есть ЛОЖЬ, а другой – ИСТИНА, то результат вычисления выражения ( Дополнительно символ НЕ существенно упрощает запись взаимоисключающих условий. Так условие расположения точки в конкретном квадранте плоскости, а тем более в пространстве, определяет очень громоздкое подробное перечисление остальных вариантов (см. начало главы). Использование символа НЕ делает взаимоисключающее условие максимально компактным, что подтверждает математическая модель нижеизложенной задачи. Рассмотрим программирование разветвляющихся вычислительных процессов с проверкой составных условий на задаче (4.2) о положении точки.
|
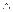– логическое умножение (И);
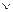– логическое сложение (ИЛИ);
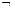– отрицание (НЕ).
