Корреляциялық функциялар.Корреляция кездейсоқ шамалар арасындағы кеңістіктік және уақыттық, немесе функцианалдық байланысты анықтайды. Динамикалық бейберекеттіктегі x i x j, - байқалған мәндер арасындағы корреляцияның ӛлшемге (x x i, 0 -арасындағы қашықтық) тәуелділігі былай анықталады.
-Хевисайд функциясы:
Такенс [6 ] х1 бір құраушы бойынша m - ӛлшемді
вектор тұрғызып, динамикалық жүйенің ӛлшемділігі туралы мағлұмат алуға болатындығын кӛрсетті. m=3 жағдайы үшін есептелген корреляция реалды үш ӛлшемді вектордың корреляцияларымен эквивалентті: lnC()-ның ln -ге тәуелділігі бірдей кӛлбеулікке ие. Практикада зерттелінетін құбылыстың ӛлшемділігін талқылау ұшін m -нің ӛсуімен жететін жоғарыдағы тәуелділіктің шектік түрі (оның қанығуы) пайдаланылады. Стохастикалық құбылыстардағы физикалық шамалар корреляциясы егер элементар қозуларды сипаттайтын аналитикалық ӛрнектер белгілі болса тікелей есептеленуі мүмкін. Бейсызық ортаның стохастизациясы кезінде солитон, құйын және т.б. түрлерде квазибӛлшектер (элементарлық қозулар) түзіледі. Олар 12 -де жекеленген жағдайлар үшін теориялық түрде анықталған. 5,13 жұмыстарда гидродинамикалық турбуленттіктің құрылымды элементтері болып табылатын құйынды солитондар үшін аналитикалық ӛрнектер табылған. Бұл ӛрнектерді ағыс функциясына тәуелді f (r,) - түрінде белгілеп, динамикалық шамалардың әртүрлі корреляцияларын есептеуге болады.
мұнда а, в -индекстері квазибӛлшектің сортын анықтайды, і,j - динамикалық шамалардың түрлерін анықтайды, r, фи- полярлық координаталар. фи- бұрышы бойынша интегралдай отырып, кеңістіктік корреляцияны табады. Бейсызық ортада әртүрлі құрылымның болуына сай (құбылысы) мәнді де қабылдайды. Бұл заңдылықтардың бҒрі де (5,14) -жұмыстарда турбуленттікті зерттеу тҒжірибелерімен дәлелденген. (5,15) формуланы пайдалана отырып, динамикалық бейберекеттіктегі тербелмелі корреляцияны (бейберекеттік пен реттіліктің алмасуы) іздестіруге назар аударуға болады.
|
(5.15)
(5.16)
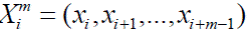(5.17)
- құраушылары бар
(5.18)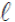
-дің ӛсуімен корреляция тербелмелі (осиллияциялы) түрде азайып, теріс
