Кинетическая энергия. 1. Диагноз: сквозное пулевое проникающее ранение правой половины грудной клетки с повреждением легкого; напряженный пневмоторакс; выраженная дыхательная
1. Диагноз: сквозное пулевое проникающее ранение правой половины грудной клетки с повреждением легкого; напряженный пневмоторакс; выраженная дыхательная недостаточность. 2. Первая помощь: асептическая повязка на обе раны; подкожно промедол из шприц-тюбика; таблетированные антибиотики; вынос в полусидящем положении, под верхнюю часть туловища подкладывают скатку шинели, вещмешок. 3. В МПП: пункция плевральной полости во втором межреберье спереди широкой иглой; правосторонняя вагосимпатическая блокада; внутримышечно 1 мл 2% раствора промедола; антибиотики, 0,5 мл столбнячного анатоксина подкожно; оксигенотерапия. 4. В ОМЕДБ: плевроцентез во втором межреберье спереди, подводный плевральный дренаж; оксигенотерапия; вагосимпатическая блокада; наркотики, антибиотики; противошоковая терапия. 5. Эвакуация в полусидящем положении на носилках в госпиталь для раненых в грудь, живот, таз.
Кинетическая энергия
Заменив в (1.5.2)
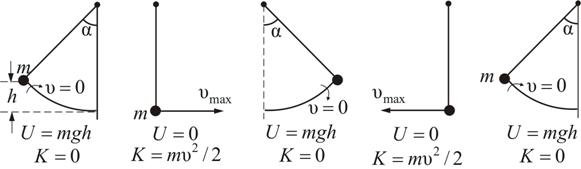
Полная механическая энергия гармонически колеблющегося тела пропорциональна квадрату амплитуды колебания. В случае свободных незатухающих колебаний полная энергия не зависит от времени, поэтому и амплитуда А не зависит от времени. Из (1.5.2) и (1.5.3) видно, что и потенциальная U,и кинетическая K энергия пропорциональны квадрату амплитуды А 2. Рассмотрим колебания груза под действием сил тяжести (рис. 1.4).
Рис. 1.4 Из рис. 1.4 и из формул (1.5.2) и (1.5.3) видно, что U и K изменяются периодически (при свободных незатухающих колебаниях). Однако период изменения энергии в два раза меньше, чем период изменения смещения скорости и ускорения. Это значит, что и кинетическая, и потенциальная энергия изменяются с частотой, которая в два раза превышает частоту смещения гармонического колебания. За время одного полного колебания U и K дважды достигают своих максимальных значений и дважды обращаются в нуль. Связано это с тем, что и U,и K пропорциональны квадрату косинуса и синуса фазы колебаний. Максимум потенциальной энергии (1.5.2) Максимум кинетической энергии
Рис. 1.5 Рис. 1.6 При колебаниях, совершающихся под действием потенциальных (консервативных) сил, происходит переход кинетической энергии в потенциальную и наоборот, но их сумма в любой момент времени постоянна. На рис. 1.6 приведена кривая потенциальной энергии. Горизонтальная линия соответствует определенному значению полной энергии: | ||||||||||
| Гармонический осциллятор |  
| |||||||||
| Математическим маятником называется идеализированная система, состоящая из невесомой нерастяжимой нити, на которую подвешена масса, сосредоточенная в одной точке (шарик на длинной тонкой нити).
Колебания гармонического осциллятора являются важным примером периодического движения и служат точной или приближенной моделью во многих задачах классической и квантовой физики. Примерами гармонического осциллятора являются: пружинный, математический и физический маятники, а также колебательный контур (для малых токов и напряжений). Пружинный маятник – это груз массой m, подвешенный на абсолютно упругой пружине с жесткостью k, совершающий гармонические колебания под действием упругой силы Уравнение движения маятника:
Из сравнения выражений (1.4.3) и (1.6.1) следует, что пружинный маятник совершает гармонические колебания по закону
Рис. 1.7 Эти формулы справедливы для упругих колебаний в пределах, когда выполняется закон Гука, т.е. когда масса пружины мала по сравнению с массой тела и ее деформация не превышает предела упругости. | |||||
| Способы представления гармонических колебаний | |||||
Гармонические колебания можно представить несколькими способами. Рассмотрим эти способы.

 Рассмотрим подробнее последний способ.
Пусть гармоническое колебание описывается уравнением x = A cos (ω t + φ0). Проведем прямую О x (опорную) и построим вектор
Рассмотрим подробнее последний способ.
Пусть гармоническое колебание описывается уравнением x = A cos (ω t + φ0). Проведем прямую О x (опорную) и построим вектор  , направленный из точки О под углом φ0 к опорной линии.
Обозначим через x 0 проекцию вектора , направленный из точки О под углом φ0 к опорной линии.
Обозначим через x 0 проекцию вектора  на опорную линию в момент времени t = 0:
x0 = A cos (φ0).
Вращение происходит против часовой стрелки, т.е. ω > 0. За промежуток времени t вектор амплитуды повернется на угол ω t и займет новое положение. Его проекция на опорную линию равна x = A cos (ω t + φ0). За время, равное периоду колебаний Т, вектор амплитуды повернется на угол 2φ, и проекция вектора совершит полное колебание около положения равновесия (точка О). Следовательно, вращающийся вектор амплитуды полностью характеризует гармоническое колебание.
Проекция кругового движения на ось у также совершает гармоническое колебание y = A sin (ω t + φ).
Таким образом, равномерное движение по окружности можно рассматривать как два колебательных гармонических движения, совершаемых одновременно в двух взаимно перпендикулярных направлениях. Этим представлением широко пользуются при сложении колебаний. на опорную линию в момент времени t = 0:
x0 = A cos (φ0).
Вращение происходит против часовой стрелки, т.е. ω > 0. За промежуток времени t вектор амплитуды повернется на угол ω t и займет новое положение. Его проекция на опорную линию равна x = A cos (ω t + φ0). За время, равное периоду колебаний Т, вектор амплитуды повернется на угол 2φ, и проекция вектора совершит полное колебание около положения равновесия (точка О). Следовательно, вращающийся вектор амплитуды полностью характеризует гармоническое колебание.
Проекция кругового движения на ось у также совершает гармоническое колебание y = A sin (ω t + φ).
Таким образом, равномерное движение по окружности можно рассматривать как два колебательных гармонических движения, совершаемых одновременно в двух взаимно перпендикулярных направлениях. Этим представлением широко пользуются при сложении колебаний.
| ||||
| Сложение гармонических колебаний одного направления и одинаковой частоты. Биения | ||||
Пусть точка одновременно участвует в двух гармонических колебаниях одинакового периода, направленных вдоль одной прямой.
Сложение колебаний будем проводить методом векторных диаграмм (рис. 2.2). Пусть колебания заданы уравнениями
Рис. 2.2 Отложим из точки О вектор Нам известно, что суммарная проекция вектора
По правилу сложения векторов найдем суммарную амплитуду:
Результирующую амплитуду найдем по формуле
Начальная фаза определяется из соотношения
Таким образом, тело, участвуя в двух гармонических колебаниях одного направления и одинаковой частоты, совершает также гармоническое колебание в том же направлении и с той же частотой, что и складываемые колебания. Из (2.2.2) следует, что амплитуда А результирующего колебания зависит от разности начальных фаз
|

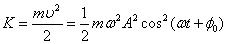 .
.
 и сложив почленно уравнения (1.5.2) и (1.5.3), получим выражение для полной энергии:
и сложив почленно уравнения (1.5.2) и (1.5.3), получим выражение для полной энергии: , или
, или .
.
 .
. , но когда
, но когда 
 и наоборот. На рис. 1.5 представлены графики зависимости х, U и K от времени t.
и наоборот. На рис. 1.5 представлены графики зависимости х, U и K от времени t.
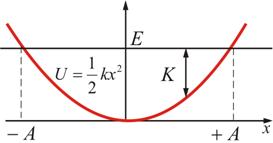
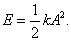 Расстояние от этой линии до кривой равно кинетической энергии, а движение ограничено значениями х, заключенными в пределах от + А до – А. Эти результаты полностью согласуются с полным решением уравнения движения.
Расстояние от этой линии до кривой равно кинетической энергии, а движение ограничено значениями х, заключенными в пределах от + А до – А. Эти результаты полностью согласуются с полным решением уравнения движения. (рис. 1.7).
(рис. 1.7). или
или  .
.
 с циклической частотой ω и периодом Т, где
с циклической частотой ω и периодом Т, где ;
; 
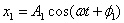 и
и 

 под углом φ1 к опорной линии и вектор
под углом φ1 к опорной линии и вектор  под углом φ2. Оба вектора вращаются против часовой стрелки с одинаковой угловой скоростью ω, поэтому их разность фаз не зависит от времени (
под углом φ2. Оба вектора вращаются против часовой стрелки с одинаковой угловой скоростью ω, поэтому их разность фаз не зависит от времени ( ). Такие колебания называют когерентными.
). Такие колебания называют когерентными. равна сумме проекций на эту же ось. Поэтому результирующее колебание может быть изображено вектором амплитуды
равна сумме проекций на эту же ось. Поэтому результирующее колебание может быть изображено вектором амплитуды  , вращающимся вокруг точки О с той же угловой скоростью ω, что и
, вращающимся вокруг точки О с той же угловой скоростью ω, что и 
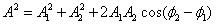 .
.
 .
.
 . Возможные значения А лежат в диапазоне
. Возможные значения А лежат в диапазоне  (амплитуда не может быть отрицательной).
(амплитуда не может быть отрицательной).


