Найдем коэффициенты a0 , a1 , a2 ,...
16. Белоконь Н.А., Кубергер М.Б. Болезни сердца и сосудов у детей. В 2-х том.- М.:Медицина, 1987. - 928 с. 17. Белозеров Ю.М. Детская кардиология (наследственные синдромы).-Элита.:ЗАОР «НПП«Джангар».-2008.-400 с. 18. Геппе Н.А. руководство по детской ревматологии// Геппе Н.А., Подчерняява Н.С., Лыскина Г.А. М.: «ГЭОТАР-Медиа».-2011.-720с:ил. 19. Геппе Н.А. Сложный больной в практике педиатра ревматолога//Геппе Н.А., Рябова Т.В. М.: ООО «Медицинское информационное агенство».-2008.-320.-с.:ил 20. Кардиология и ревматология детского возраста /Под ред. Г.А.Самсыгиной и М.Ю.Щербаковой. – М.: ИД Медпрактика. – М., 2004. - 774 с. 21. Коровина Н.А., Гаврюшова Л.П., Творогова Т.М. Вегетативные дистонии у детей /пособие для врачей/ М., 2000. - 62 с. 22. Крючко Т.О., Пеший М.М., Танянська С.М. Дитяча кардіологія (частина ІІ). Навчальний посібник. – Полтава, 2007.- 175с. 23. Леженко Г.О., Волосовець О.П., Кривопустов С.П., Прохоров Є.В., Пашкова О.Є., Подліанова О.І. Синдром недиференційованої дисплазії сполучної тканини у дітей та підлітків (поширеність, особливості діагностики та лікування). Монографія. – Запоріжжя: Видавництво Запорізького державного медичного університету, 2006. – 134 с. 24. Макаров Л.М. Холтеровское мониторирование. М.: Медпрактика. - 2000. - 213 с. 25. Мутафьян О.А. Артериальные гипертензии и гипотензии у детей и подростков. –Спб.: Невский диалект, М.:Издательство БИНОМ, 2002. – 144 с. 26. Мутафьян О.А. Пороки и малые аномалии сердца у детей и подростков / СПб.: Издательский дом СПб МАПО, 2005. – 480 с. 27. Педіатричні аспекти ведення дітей з природженими вадами серця. Навчальний посібник для студентів ВМНЗ IV рівня акредитації та лікарів-інтернів / За ред. О.П. Волосовця, Г.С. Сенаторової, М.О. Гончарь. – Тернопіль: ТДМУ, 2008. – 176 с. 28. Пєший М.М. Дитяча кардіологія /Клінічні лекції/. Полтава. - 2006. – 194 с. 29. Рыбакова М.К., Алехин М.Н., Митьков В.В. Практическое руководство по ультразвуковой диагностике. Эхокардиография. Издание 2-е. ВИДАР, 2008г. -544 с. 30. Середа Ю.В. Электрокардиография в педиатрии: Учебное пособие. Спб.: «Элби-Спб», - 2004. – 101 с.
Найдем коэффициенты a0, a1, a2,... Положим в равенстве (1)
Продифференцируем ряд (1)
и вновь положим
Проводя дальнейшее дифференцирование и полагая лучим следующие равенства
Таким образом находятся все коэффициенты разложения (1):
Подставляя найденные коэффициенты (2) в равенство (1) получим разложение функции ра для функции
Коэффициенты (2) называются коэффициентами Тейлора функции точке a. Ряд (3), записанный в окрестности нуля, когда вают рядом Маклорена:
III. Разложение по степеням x функций ex, Разложение функции в ряд Тейлора в окрестности точки a рас- падается на два этапа: 1) вычисляют значения функции ке a и находят коэффициенты ряда Тейлора (2) 2) определяют интервал, в котором составленный ряд Тейлора схо- дится к функции Найдем разложение в ряд Маклорена следующих элементарных функ- ций:
1) показательная функция ex.
В точке Ряд Маклорена для показательной функции:
Рассмотрим интервал рованное число. Для любого X из этого интервала Следовательно, все производные в этом интервале ограничены и
ex на всей числовой оси 2) тригонометрические функции Пусть
и т.д. Любая производная от чине 1, поэтому ряд Маклорена для функции дится к ней на всей числовой оси:
Аналогично можно получить разложение на всей числовой оси:
3) биномиальный ряд - разложение в ряд Маклорена функции
………………………………………………….
Тогда
Найдем область сходимости ряда (10), пользуясь признаком Даламбера для функциональных рядов:
Таким образом, ряд (10) сходится на интервале ции 4) функция Запишем ряд Маклорена для функции равенством (10) и принимая
и воспользуемся возможностью интегрирования степенных рядов в облас- ти их сходимости:
Тогда интегрируя ряд (*), получим разложение в ряд функции справедливое на интервале
5) функция Запишем ряд для функции x на x2:
.и проинтегрируем последнее соотношение:
Соотношение (12) представляет собой разложение в ряд Маклорена для функции Степенные ряды (7)-(12) можно использовать при разложении в ряд многих других функций. Например, разложения для гиперболических функций могут быть получены комбинацией рядов для ex и e-x:
V. Приложения рядов Тейлора. Разложения функций в степенные ряды используется при приближен- ных вычислениях значений функции, при интегрировании функций и реше- нии дифференциальных уравнений. 1) Пусть нам известны значения функции и ее производных в неко- торой точке a, и функция ряд Тейлора. Тогда точное значение функции в рассматриваемой окрестности можно вычислить по ряду Тейлора, а приближенно ее значение - по частичной сумме этого ряда. Возникающую при этом ошибку оценивают по остаточному члену ряда или непосредственно по остатку ряда. Если получающийся числовой ряд знакочередующийся, то в соответствии с теоремой Лейбница остаток ряда не превосходит величины первого из отбрасываемых членов. При вычислениях оценивают по величине первого из отброшенных членов. Так
Если требуемая точность вычисления вой формулой можно пользоваться в интервале от 0 до второй - от 2) интегрирование функций с помощью рядов. Допустим, что нужно найти интеграл
причем известно разложение функции делы интегрирования лежат внутри интервала сходимости ряда. Тогда мы имеем право интегрировать ряд почленно. В результате получится ряд для функции ральная функция. Если при этом интеграл выражается через элементарную функцию, то мы сможем получить для нее разложение в ряд Тейлора, как в случа- ях для в элементарных функциях, то найденный ряд служит выражением неэле- ментарной функции через бесконечную сумму степенных функций, напри- мер:
Этот ряд не сходится ни к одной элементарной функции, а служит выражением новой функции, определенной на всей числовой оси.
|

 , тогда
, тогда


 ;
;  ;
; 



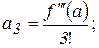

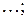
 (2)
(2) в ряд, который называется рядом Тейло-
в ряд, который называется рядом Тейло- (3)
(3) назы-
назы-

 ,
,  ,(1+ x ) n,
,(1+ x ) n,  ,
,  .
.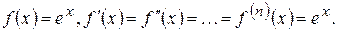
 функция и все ее производные равны 1.
функция и все ее производные равны 1. (7)
(7) , где N - любое фикси-
, где N - любое фикси-
 Таким образом, ряд (7) сходится к функции
Таким образом, ряд (7) сходится к функции .
.
 не превосходит по абсолютной вели-
не превосходит по абсолютной вели- схо-
схо-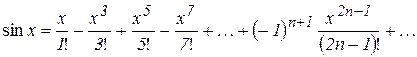

 , где m - любое действительное число.
, где m - любое действительное число. ,
, 
 ,
, 
 ,
, 

 (10)
(10)

 к функ-
к функ-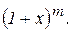 .
.
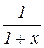 , пользуясь
, пользуясь .
. (*)
(*)

 (11)
(11)
 , заменяя в равенстве (*)
, заменяя в равенстве (*)

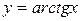 , сходящееся к ней на интервале
, сходящееся к ней на интервале 








 , то пер-
, то пер- ;
; ; третьей - от
; третьей - от  .
.
 , сходящейся в том же интервале, что и подынтег-
, сходящейся в том же интервале, что и подынтег-





