| 7.1. Функціональний зв’язок – це зв’язок, при якому:
|
| a) одному значенню одного показника (X) відповідає цілком визначене одне значення іншого показника (Y), тобто Y= f(X);
| b) кожному значенню величини X, із множини її можливих значень, відповідає певний розподіл можливих значень величини Y;
|
| c) зміна величини X призводить до зміни розподілу значень величини Y;
| d) зміна величини X викликає зміну математичного сподівання Y.
|
| 7.2. Статистична залежність – це залежність, при якій:
|
| a) одному значенню одного показника (X) відповідає цілком визначене одне значення іншого показника (Y), тобто Y= f(X);
| b) кожному значенню величини X, із множини її можливих значень, відповідає певний розподіл можливих значень величини Y;
|
| c) зміна величини X призводить до зміни розподілу значень величини Y;
| d) зміна величини X викликає зміну математичного сподівання Y.
|
| 7.3. Кореляційна залежність – це залежність, при якій:
|
| a) одному значенню одного показника (X) відповідає цілком визначене одне значення іншого показника (Y), тобто Y= f(X);
| b) кожному значенню величини X, із множини її можливих значень, відповідає певний розподіл можливих значень величини Y;
|
| c) зміна величини X призводить до зміни розподілу значень величини Y;
| d) зміна величини X викликає зміну математичного сподівання Y.
|
| 7.4. Коефіцієнт кореляції визначають за формулою:
|
a)  ; ;
| b)  ; ;
|
c)  ; ;
| d)  . .
|
7.5. Якщо 0,7<   1, то кореляційний зв’язок: 1, то кореляційний зв’язок:
|
| a) сильний;
| b) середній;
|
| c) слабкий;
| d) відсутній.
|
7.6. Якщо 0,5<   0,7, то кореляційний зв’язок: 0,7, то кореляційний зв’язок:
|
| a) сильний;
| b) середній;
|
| c) слабкий;
| d) тісний.
|
7.7. Якщо 0<   0,5, то кореляційний зв’язок: 0,5, то кореляційний зв’язок:
|
| a) сильний;
| b) середній;
|
| c) слабкий;
| d) тісний.
|
7.8. Якщо  >0, то зв’язок: >0, то зв’язок:
|
| a) прямий;
| b) від’ємний;
|
| c) зворотній.
|
|
7.9. Якщо  <0, то зв’язок: <0, то зв’язок:
|
| a) прямий;
| b) додатній;
|
| c) зворотній.
|
|
| 7.10. Кореляційне поле можна отримати, якщо:
|
| a) нанести на координатну площину ХОУ відповідні пари значень х і у;
| b) для довільної сукупності нанести на координатну площину ХОУ відповідні пари значень х і у;
|
| c) для генеральної сукупності нанести на координатну площину ХОУ відповідні пари значень х і у;
| d) для статистичної сукупності нанести на координатну площину ХОУ відповідні пари значень х і у.
|
| 7.11. Лінія регресії – це:
|
| a) лінія, яка проходить через множину точок кореляційного поля і забезпечує мінімальну суму квадратів відхилень всіх точок від даної лінії;
| b) лінія, яка проходить через множину точок кореляційного поля і забезпечує максимальну суму квадратів відхилень всіх точок від даної лінії;
|
| c) лінія, яка проходить через дві довільні точки кореляційного поля і забезпечує мінімальну суму квадратів відхилень всіх точок від даної лінії.
|
| 7.12. Рівняння лінійної регресії:
|
a)  ; ;
| b)  ; ;
|
c)  ; ;
| d)  . .
|
| 7.13. Коефіцієнт регресії визначається як:
|
a)  ; ;
| b)  ; ;
|
c) 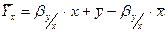 ; ;
| d)  . .
|
7.14. Якщо  , то кореляційний зв’язок: , то кореляційний зв’язок:
|
| a) відсутній;
| b) наближається до лінійного функціонального зв’язку;
|
| c) парний;
| d) непарний.
|
7.15. Якщо 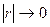 , то кореляційний зв’язок: , то кореляційний зв’язок:
|
| a) відсутній;
| b) наближається до лінійного функціонального зв’язку;
|
| c) парний;
| d) непарний.
|
| 7.16. Нормованим відхиленням значення випадкової величини хі є:
|
a) 
| b) 
|
c) 
| d) 
|
| 7.17. При розрахунках коефіцієнта кореляції отриманий результат r = 1,15. Який слід зробити висновок?
|
| a) зв’язок між величинами відсутній.
| b) зв’язок між величинами тісний і прямий.
|
| c) зв’язок між величинами тісний і зворотній.
| d) помилка при розрахунках.
|
| 7.18. Коефіцієнт Стьюдента для оцінки достовірності коефіцієнта кореляції визначається за формулою:
|
a)  ; ;
| b)  ; ;
|
c) 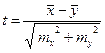 ; ;
| d)  . .
|
| 7.19. Рівняння регресії дає можливість:
|
| a) визначити значення одного показника за відомою величиною іншого показника.
| b) оцінити середні значення двох показників.
|
| c) встановити аналогію між кореляційним і функціональним зв’язками величин.
| d) оцінити середнє значення одного показника за відомою величиною іншого взаємозв’язаного показника.
|
| | | | | |