| 5.1. Елементарними називають події, які:
|
| a) є сумісними;
| b) є несумісними;
|
| c) є неможливими або достовірними;
| d) утворюють повну групу подій;
|
| e) утворюють повну групу попарно несумісних і рівноможливих подій.
|
5.2. В урні є 7 чорних і декілька білих кульок. Ймовірність появи чорної кульки дорівнює  . Яка кількість білих кульок в урні? . Яка кількість білих кульок в урні?
|
| a) 42;
| b) 35;
|
| c) 7;
| d) 5.
|
| 5.3. В деяку лікарню поступають хворі з 4 видами захворювань, ймовірність яких відповідно дорівнює 0,1; 0,4; 0,3; 0,2. Для лікування першого і четвертого захворювань необхідно переливання крові. Яку кількість хворих необхідно забезпечити кров’ю із 1000 хворих, які поступають в лікарню протягом місяця.
|
| a) 300;
| b) 500;
|
| c) 700;
| d) 900.
|
| 5.4. За якою формулою визначається математичне сподівання неперервної випадкової величини?
|
a) 
| b) 
|
c) 
| d) 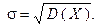
|
| 5.5. Вкажіть, які з приведених співвідношень виражають нормальний закон розподілу:
|
a) 
| b) 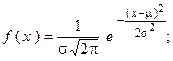
|
c) 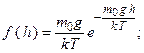
| d) 
|
| 5.6. Багаторічний досвід показує, що ймовірність виклику швидкої медичної допомоги в деякий мікрорайон складає 0,4. Знайти ймовірність того, що з п’яти викликів швидкої допомоги лікаря два будуть в даний мікрорайон.
|
| a) 0,346;
| b) 0,464;
|
| c) 0,643;
| d) 0,918.
|
| 5.7. Заданий закон розподілу випадкової величини
|
|
|
| Знайти математичне сподівання.
|
| a) 2,8;
| b) 5,1;
|
| c) 3,3;
| d) 2,02.
|
| 5.8. Випадкова величина розподілена за стандартним законом розподілу (m = 0; s = 1). Знайти ймовірність того, що випадкова величина приймає значення на інтервалі (– 1; 1).
|
| a) 0,19;
| b) 0,41;
|
| c) 0,95;
| d) 0,68.
|
| 5.9. Випадкова подія – це:
|
| a) подія, яка при заданому комплексі умов ніколи не відбудеться;
| b) подія, яка при заданому комплексі умов може як відбутися, так і не відбутись;
|
| c) подія, яка при заданому комплексі умов обов’язково відбудеться;
| d) змінна величина, яка може приймати ті чи інші числові значення з певними ймовірностями, в залежності від випадкового збігу обставин.
|
| 5.10. Сумісними називають випадкові події, якщо:
|
| a) вони утворюють повну групу попарно несумісних і рівноможливих подій;
| b) поява однієї із них в результаті випробовування виключає появу іншої в тому ж випробуванні;
|
| c) поява однієї із них в результаті випробовування не виключає повністю появу іншої в тому ж випробуванні;
| d) подія, яка при заданому комплексі умов обов’язково відбудеться.
|
| 5.11. Несумісними називають випадкові події, якщо:
|
| a) вони утворюють повну групу попарно несумісних і рівноможливих подій;
| b) поява однієї із них в результаті випробовування виключає появу іншої в тому ж випробуванні;
|
| c) поява однієї із них в результаті випробовування не виключає повністю появу іншої в тому ж випробуванні;
| d) подія, яка при заданому комплексі умов обов’язково відбудеться.
|
| 5.12. Теорема множення ймовірностей незалежних подій:
|
| a) Р(АВ)=Р(А)·Р(В);
| b) Р(АВ)= Р(А)·Р(В/А);
|
| c) Р(А+В)=Р(А)+Р(В);
| d) Р(В/А)=  . .
|
| 5.13. Теорема множення ймовірностей залежних подій:
|
| a) Р(АВ)=Р(А)·Р(В);
| b) Р(АВ)= Р(А)·Р(В/А);
|
| c) Р(А+В)=Р(А)+Р(В);
| d) Р(В/А)=  . .
|
| 5.14. Теорема додавання ймовірностей несумісних подій:
|
| a) Р(АВ)=Р(А)·Р(В);
| b) Р(АВ)= Р(А)·Р(В/А);
|
| c) Р(А+В)=Р(А)+Р(В);
| d) Р(В/А)= 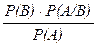 . .
|
| 5.15. Випадкова величина – це:
|
| a) величина, яка приймає окремі можливі значення з певними ймовірностями;
|
| b) величина, яка приймає довільні значення і з деякого скінченного або нескінченного інтервалу;
|
| c) величина, значення якої можна пронумерувати;
|
| d) змінна величина, яка може приймати ті чи інші числові значення з певними ймовірностями, в залежності від випадкового збігу обставин.
|
| 5.16. Дискретна випадкова величина:
|
| a) величина, яка приймає окремі можливі значення з певними ймовірностями;
|
| b) величина, яка приймає довільні значення і з деякого скінченого або нескінченного інтервалу;
|
| c) величина, яка може приймати в залежності від випадкового збігу обставин ті чи інші числові значення з певними ймовірностями;
|
| d) величина, значення якої не можна пронумерувати.
|
| 5.17. Неперервна випадкова величина:
|
| a) величина, яка приймає окремі можливі значення з певними ймовірностями;
|
| b) величина, яка приймає довільні значення і з деякого скінченого або нескінченного інтервалу;
|
| c) величина, яка може приймати в залежності від випадкового збігу обставин ті чи інші числові значення з певними ймовірностями;
|
| d) величина, значення якої можна пронумерувати.
|
| 5.18. Правило “3σ” формулюється:
|
a) неперервна випадкова величина Х, яка розподілена за нормальним законом з ймовірністю Р = 0,997 приймає значення в інтервалі 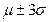 ; ;
|
b) дискретна випадкова величина Х, яка розподілена за нормальним законом з ймовірністю Р = 0,997 приймає значення в інтервалі 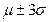 ; ;
|
c) значення дискретної випадкової величини Х, яка розподілена за нормальним законом з ймовірністю Р = 0,997 не виходять за інтервал 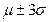 . .
|
| 5.19. Умовна ймовірність визначається за формулою:
|
a)  ; ;
| b)  ; ;
|
c)  ; ;
| d)  = =  ; ;
|
e)  . .
|
| 5.20. Теорія ймовірностей – це наука, яка вивчає:
|
| a) властивості масових випадкових подій, які можуть багаторазово повторюватись при виконанні певного комплексу умов;
|
| b) методи опису і аналізу експериментальних даних, отриманих в результаті вивчення масових випадкових явищ;
|
| c) механічні властивості живих тканин, органів і організму в цілому, а також механічні явища, що відбуваються в них у процесі життєдіяльності;
|
| d) процеси плину біологічних рідин, деформації клітин, тканин і органів.
|
| 5.21. Інтегральна теорема Муавра – Лапласа записується як:
|
a) 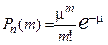 ; ;
| b)  ; ;
|
c) 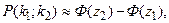 де де  , , 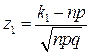 , ,  ; ;
|
d)  , де , де  , , 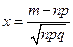 . .
|
| 5.22. Випробуванням називають:
|
| a) здійснення деякого комплексу умов, який може бути повтореним як завгодно велике число разів;
| b) явище, яке відбувається при наявності певного комплексу умов;
|
| c) подія, яка при заданому комплексі умов ніколи не відбудеться;
| d) подія, яка обов’язково відбудеться при наявності певного комплексу умов.
|
| 5.23. Подією називається:
|
| a) результат здійснення деякого комплексу умов, який може бути повтореним як завгодно велике число разів;
| b) явище, яке відбувається при наявності певного комплексу умов;
|
| c) подія, яка при заданому комплексі умов ніколи не відбудеться;
| d) подія, яка обов’язково відбудеться при наявності певного комплексу умов.
|
| 5.24. Достовірна подія це:
|
| a) подія, в якій здійснюється виконання деякого комплексу умов, який може бути повтореним як завгодно велике число разів;
| b) подія, яка відбувається при наявності певного комплексу умов;
|
| c) подія, яка при заданому комплексі умов ніколи не відбудеться;
| d) подія, яка обов’язково відбудеться при наявності певного комплексу умов.
|
| 5.25. Неможлива подія це:
|
| a) подія, в якій здійснюється виконання деякого комплексу умов, який може бути повтореним як завгодно велике число разів;
| b) подія, яка відбувається при наявності певного комплексу умов;
|
| c) подія, яка при заданому комплексі умов ніколи не відбудеться;
| d) подія, яка обов’язково відбудеться при наявності певного комплексу умов.
|
| 5.26. Класичне означення ймовірності випадкової події:
|
| a) ймовірністю Р(А) події А називають відношення числа елементарних подій, за яких подія А відбувається, до числа всіх можливих елементарних подій;
|
b) ймовірністю називають відношення  , якщо в n випробуваннях, проведених при рівних умовах, подія А мала місце m разів; , якщо в n випробуваннях, проведених при рівних умовах, подія А мала місце m разів;
|
| c) границя, до якої прямує відносна частота появи події при необмеженому збільшені кількості випробувань;
|
| d) ймовірність практично дорівнює частоті появи події при великій кількості випробувань проведених при однакових умовах.
|
| 5.27. Відносна частота появи події це:
|
| a) ймовірністю Р(А) події А називають відношення числа елементарних подій, за яких подія А відбувається, до числа всіх можливих елементарних подій;
|
b) відношення  , якщо в n випробуваннях, проведених при рівних умовах, подія А мала місце m разів; , якщо в n випробуваннях, проведених при рівних умовах, подія А мала місце m разів;
|
| c) границя, до якої прямує частота появи події при необмеженому збільшені кількості випробувань;
|
| d) ймовірність появи події при великій кількості випробувань проведених при однакових умовах.
|
| 5.28. Статистичне означення ймовірності випадкової події:
|
| a) ймовірністю Р(А) події А називають відношення числа елементарних подій, за яких подія А відбувається, до числа всіх можливих елементарних подій;
|
b) це відношення  , якщо в n випробуваннях, проведених при рівних умовах, подія А мала місце m разів; , якщо в n випробуваннях, проведених при рівних умовах, подія А мала місце m разів;
|
| c) границя, до якої прямує відносна частота появи події при необмеженому збільшені кількості випробувань;
|
| d) ймовірність практично дорівнює частоті появи подій при великій кількості випробувань проведених при однакових умовах.
|
| 5.29. За якою формулою визначається дисперсія дискретної випадкової величини?
|
a) 
| b) 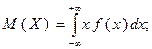
|
c) 
| d) 
|
| 5.30. За якою формулою визначається середнє квадратичне відхилення випадкової величини?
|
a) 
| b) 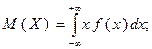
|
c) 
| d) 
|
| 5.32. Теорема додавання ймовірностей сумісних подій:
|
a)  ; ;
| b) 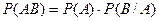 ; ;
|
c) 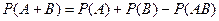 ; ;
| d)  . .
|
| 5.33. Вкажіть, які з поданих співвідношень виражають розподіл Бернуллі:
|
a) 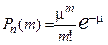 ; ;
| b)  ; ;
|
c)  де де  , , 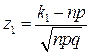 , ,  ; ;
|
d)  , де , де  , , 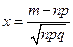 . .
|
| 5.34. Вкажіть, які з поданих співвідношень виражають розподіл Пуассона?
|
a) 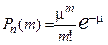 ; ;
| b)  ; ;
|
c)  де де  ; ;
|
d)  , де , де  . .
|
| 5.35. Вкажіть, які з поданих співвідношень виражають локальну теорему Муавра – Лапласа?
|
a) 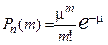 ; ;
| b)  ; ;
|
c)  де де  ; ;
|
d)  , де , де  . .
|
| 5.36. Подія В називається залежною від події А, якщо
|
| a) ймовірність події В залежить від того, відбулась чи ні подія А;
| b) ймовірність появи події В не залежить від того відбулась чи не відбулась подія А;
|
| c) поява однієї із них в результаті випробовування виключає повністю появу іншої в тому ж випробуванні;
| d) поява однієї із них в результаті випробовування не виключає повністю появу іншої в тому ж випробуванні.
|
| 5.37. Ймовірність появи хоча б однієї події А із сукупності незалежних подій А1, А2, …, Аn визначається за формулою:
|
a)  ; ;
| b) 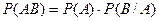 ; ;
|
c)  ; ;
| d)  . .
|
| 5.38. На основі умови нормування:
|
a) 
| b) 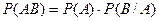
|
c) 
| d) 
|
| 5.39. Дві події називають протилежними, якщо:
|
| a) вони несумісні і утворюють повну групу;
|
| b) поява однієї із них в результаті випробовування виключає повністю появу іншої в тому ж випробуванні;
|
| c) вони утворюють повну групу попарно несумісних і рівноможливих подій;
|
| d) поява однієї із них в результаті випробовування не виключає повністю появу іншої в тому ж випробуванні.
|
| 5.40. Дві події А і В називаються незалежними, якщо
|
| a) ймовірність появи події А не залежить від того відбулась чи не відбулась подія В;
| b) вони утворюють повну групу попарно несумісних і рівноможливих подій;
|
| c) поява однієї із них в результаті випробовування виключає повністю появу іншої в тому ж випробуванні;
| d) поява однієї із них в результаті випробовування не виключає повністю появу іншої в тому ж випробуванні.
|
5.41. У відділенні три операційні. Для кожної з них ймовірність бути зайнятою (не бути вільною) в даний момент часу  . Яка ймовірність, що хоча б одна операційна вільна в даний момент? . Яка ймовірність, що хоча б одна операційна вільна в даний момент?
|
| a) 0,973;
| b) 0,937;
|
| c) 0,739;
| d) 0,397.
|
| 5.42. Формула повної ймовірності записується у такому вигляді:
|
a)  ; ;
| b)  ; ;
|
c)  ; ;
| d)  = =  ; ;
|
e)  . .
|
| 5.43. Переоцінка ймовірності гіпотез за умови, що подія А відбулась, проводиться за формулою Байєса:
|
a)  ; ;
| b)  ; ;
|
c) 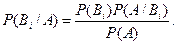
|
|
| 5.44. З врахуванням формули повної ймовірності співвідношення Байєса набуває вигляду:
|
a)  ; ;
| b)  ; ;
|
c) 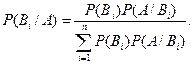
|
|
| 5.45. Сума ймовірностей гіпотез В1, В2, …, Вn, як повної групи подій, повинна дорівнювати
|
| a) 1;
| b) 0;
|
| c) -1.
|
|
| 5.46. За якою формулою визначається дисперсія неперервної випадкової величини?
|
a) 
| b) 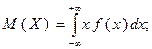
|
c) 
| d) 
|
| 5.47. За якою формулою визначається математичне сподівання дискретної випадкової величини?
|
a) 
| b) 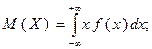
|
c) 
| d)  . .
|
| 5.48. Умова нормування для дискретної випадкової величини:
|
a) 
| b) 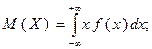
|
c) 
| d) 
|
| 5.49. Умова нормування для неперервної випадкової величини:
|
a) 
| b) 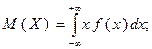
|
c) 
| d) 
|
| 5.50. Модою М0(Х) дискретної випадкової величини Х називають:
|
| a) таке значення xm випадкової величини, що попереднє і наступне за ним значення мають ймовірності, менші від Р(xm);
| b) таке значення xm випадкової величини, що попереднє і наступне за ним значення мають ймовірності, більші від Р(xm);
|
| c) таке значення xm випадкової величини, що попереднє і наступне за ним значення мають ймовірності рівні нулю;
| d) таке значення xm випадкової величини, що попереднє і наступне за ним значення мають ймовірності рівні одиниці.
|
| | | | | | |