| 6.1. Вибірка, здійснена з генеральної сукупності, повинна бути:
|
| a) великою;
| b) малою;
|
| c) будь–якою;
| d) випадковою;
|
| e) повторною;
| f) безповторною.
|
| 6.2. Генеральне середнє і математичне сподівання випадкової величини є:
|
| a) рівними величинами;
| b) наближено рівними величинами;
|
| c) довільними незалежними величинами
|
|
| 6.3. Розподіл Стьюдента:
|
| a) наближається до нормального закону розподілу для вибірки невеликого об’єму;
| b) наближається до нормального закону розподілу для великих вибірок;
|
| c) дає змогу розрахувати коефіцієнт Стьюдента;
| d) встановлює зв’язок між густиною ймовірності нормованого відхилення і об’ємом вибірки.
|
| 6.4. Надійним називають інтервал, в якому:
|
| a) знаходиться вибіркове середнє випадкової величини;
| b) з надійною ймовірністю (Р ³ 0,95) знаходиться генеральне середнє випадкової величини;
|
| c) з надійною ймовірністю (Р ³ 0,95) знаходиться вибіркове середнє випадкової величини;
| d) заданий розподіл можливих значень випадкової величини.
|
| 6.5. Вкажіть правильну форму запису надійного інтервалу:
|
a)  ;
| b)  ;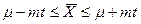
|
c)  ,
|
|
| 6.6. Математична статистика вивчає:
|
| a) властивості масових випадкових подій, які можуть багаторазово повторюватись при виконанні певного комплексу умов;
| b) методи опису і аналізу експериментальних даних, отриманих в результаті вивчення масових випадкових явищ;
|
| c) механічні властивості живих тканин, органів і організму в цілому, а також механічні явища, що відбуваються в них у процесі життєдіяльності;
| d) процеси плину біологічних рідин, деформації клітин, тканин і органів.
|
| 6.7. Генеральна сукупність:
|
| a) множина об’єктів, однорідних відносно деякої якісної або кількісної ознаки, характерної для даних об’єктів;
| b) сукупність, яка включає всі об’єкти які можуть бути до неї віднесені;
|
| c) множина об’єктів, неоднорідних відносно деякої якісної або кількісної ознаки, характерної для даних об’єктів;
| d) множина об’єктів, випадково відібраних із статистичної сукупності.
|
 6.8. За якою схемою за таблицею розподілу Стьюдента оцінюється достовірність різниці генеральних середніх:
де  – генеральне середнє;  – вибіркові середні; m – математичне сподівання; m – стандартна похибка; t – коефіцієнт Стьюдента.
|
| 6.9. Вибірка репрезентативна, якщо:
|
| a) здійснена випадково;
| b) здійснена невипадково, а за певним законом;
|
| c) при відборі всі елементи мали нерівну ймовірність попасти у вибірку.
|
|
| 6.10. Оцінку достовірності різниці генеральних середніх проводять за формулою:
|
a)  ;
| b)  ;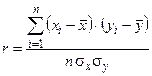
|
c)  ;
| d)  .
|
| 6.11. Стандартну похибку (n < 30) визначають за формулою:
|
a)  ;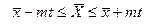
| b) ;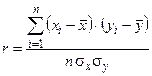
|
| c) ;
| d) .
|
| 6.12. Статистична сукупність:
|
| a) множина об’єктів, однорідних відносно деякої якісної або кількісної ознаки, характерної для даних об’єктів;
| b) сукупність, яка включає всі об’єкти які можуть бути до неї віднесені;
|
| c) множина об’єктів, неоднорідних відносно деякої якісної або кількісної ознаки, характерної для даних об’єктів;
| d) множина об’єктів, випадково відібраних із генеральної сукупності.
|
| 6.13. Вибірки поділяють на:
|
| a) парні і непарні;
| b) від’ємні і додатні;
|
| c) малі і великі;
| d) повторювані і періодичні.
|
| 6.14. За якою формулою обчислюються генеральне середнє?
|
a) 
| b) 
|
c) 
|
|
