| 1.1. Біофізика – це наука, що вивчає...
|
| a) фізичні і фізико–хімічні процеси, що відбуваються у біологічних системах на різних рівнях організації;
| b) властивості і структуру біологічних речовин, а також їх взаємодії;
|
| c) живі об’єкти фізичними експериментами;
| d) фізіологічні процеси в біооб’єктах.
|
| 1.2. Функція однієї змінної y=f(x) – це функція, в якій
|
| a) кожному х відповідає довільне значення функції у;
| b) кожному х за певним законом відповідає набір значень функції у;
|
| c) кожному х за певним законом відповідає єдине значення функції у;
| d) зміна значення функції у залежить від зміни значення х.
|
| 1.3. Область визначення функції y=f(x) – це
|
| a) всі значення х, для яких функція у визначена;
| b) всі значення х, при яких функція y не існує;
|
| c) значення функції у, при х →0; х → ±∞;
| d) всі значення функції у, які відповідають набору всіх можливих значень f.
|
| 1.4. Похідна функцій y=f(x) – це
|
| a) відношення приросту функції до приросту аргументу;
| b) відношення приросту аргументу до приросту функції;
|
| c) границя відношення приросту функції до приросту аргументу;
| d) границя відношення приросту аргументу до приросту функції;
|
| e) границя відношення приросту функції до приросту аргументу при умові, що приріст аргументу прямує до нуля;
| f) границя відношення приросту аргументу до приросту функції при умові, що приріст функції прямує до нуля.
|
| 1.5. Геометричний зміст похідної:
|
| a) чисельно дорівнює тангенсу кута, який утворює дотична до графіка функції в даній точці з віссю ОХ;
| b) чисельно дорівнює тангенсу кута, який утворює січна до графіка функції з віссю ОХ;
|
| c) чисельно дорівнює куту нахилу дотичної до графіка функції в деякій точці;
| d) чисельно дорівнює приросту ординати дотичної;
|
| e) чисельно дорівнює приросту абсциси.
|
|
| 1.6. Похідна від добутку двох функцій визначається за формулою:
|
a)  ;
| b)  ;
|
c)  ;
| d) 
|
| 1.7. Похідна другого порядку – це
|
a)  – похідна першого порядку до квадрату;
| b)  – сума похідних першого порядку;
|
c) 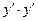 – добуток похідних першого порядку;
| d)  похідна від похідної першого порядку.
|
| 1.8. Критичні точки функції – це точки, в яких
|
| a) значення функції дорівнює нулю або не існує;
| b) значення похідної функції дорівнює нулю або не існує;
|
| c) значення похідної функції є максимальним;
| d) значення похідної функції є мінімальним;
|
| e) значення функції є максимальним або мінімальним.
|
| 1.9. Необхідною умовою екстремуму функції y=f(x) в точці х=хк є виконання умови
|
| a) хк додатне число;
| b) хк від’ємне число;
|
| c) хк має бути відмінним від нуля;
| d)  ;
|
e)  ;
| f)  .
|
| 1.10. Функція y=f(x) має мінімум в точці х = хк, якщо
|
a)  ;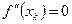
| b)  змінює знак при переході через хк з “–” на “+”;
|
c)  ;
| d) змінює знак при переході через хк з “+” на “–”;
|
e)  ;
| f)  змінює знак при переході через хк з “–” на “+”.
|
| 1.11. Функція y=f(x) має максимум в точці х = хк, якщо
|
| a) ;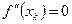
| b) змінює знак при переході через хк з “–” на “+”;
|
| c) ;
| d) змінює знак при переході через хк з “+” на “–”;
|
| e) ;
| f) змінює знак при переході через хк з “+” на “–”.
|
| 1.12. Точка х = хк є точкою перегину, якщо
|
a)  ;
| b)  ;
|
| c) ;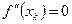
| d) ;
|
| e) .
|
|
| 1.13. Функція y=f(x) на відрізку [a; b] зростає, якщо на цьому відрізку вона неперервна і
|
a)  ;
| b)  ;
|
c)  ;
| d)  ;
|
e)  ;
| f)  .
|
| 1.14. Функція y=f(x) на відрізку [a; b] спадає, якщо на цьому відрізку
|
| a) ;
| b) ;
|
| c) ;
| d) ;
|
| e) ;
| f) .
|
1.15. Обчислити похідну функції 
|
a)  ;
| b)  ;
|
c)  ;
| d)  .
|
1.16. Обчислити похідну функції  :
|
a)  ;
| b)  ;
|
c)  ;
| d)  .
|
1.17. Обчислити похідну функції  :
|
a)  ;
| b)  ;
|
c)  ;
| d)  .
|
1.18. Обчислити похідну функції  :
|
a)  ;
| b)  ;
|
c)  ;
| d)  .
|
1.19. Обчислити похідну функції  :
|
a)  ;
| b)  ;
|
c)  ;
| d)  .
|
1.20. Обчислити другу похідну функції  :
|
a)  ;
| b)  ;
|
c)  ;
| d)  .
|
1.21. Обчислити похідну функції  :
|
a)  ;
| b)  ;
|
c)  ;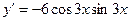
| d)  .
|
1.22. Обчислити похідну функції  :
|
a)  ;
| b)  ;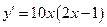
|
c)  ;
| d)  .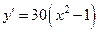
|
| 1.23. Похідна частки двох функцій визначається за формулою:
|
a) 
| b)  ;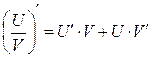
|
c)  ;
| d) 
|
| 1.24. Похідна алгебраїчної суми двох функцій визначається за формулою:
|
a) 
| b)  ;
|
c)  ;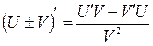
| d) 
|
| | | | |
