| 4.1. Диференціальним рівнянням називають:
|
| a) рівняння, яке містить диференціал функції;
| b) рівняння, яке містить похідну функції;
|
| c) рівняння, яке містить незалежну змінну х, шукану функцію у=f(x) і її похідні у', у'',..., у(n);
| d) будь–яке рівняння.
|
| 4.2. Символічно диференціальне рівняння записують:
|
| a) F(x, y, у', у'',..., у(n))= 0;
| b) F (x, y, yn)= 0;
|
| c) F (x, y)= 0;
| d) F (у', у'',..., у(n))= 0.
|
| 4.3. Диференціальне рівняння називається звичайним, якщо:
|
| a) шукана функція у=f(x) є функцією однієї незалежної змінної;
| b) шукана функція у=f(x) є функцією двох і більше аргументів;
|
| c) дане рівняння не містить похідної у'(х);
| d) дане рівняння не містить незалежної змінної х.
|
| 4.4. Диференціальним рівнянням в частинних похідних називають рівняння, в якому:
|
| a) міститься будь–яка частинна похідна;
| b) шукана функція у=f(x) є функцією однієї незалежної змінної;
|
| c) шукана функція у=f(x) є функцією двох і більше аргументів;
| d) немає незалежної змінної х.
|
| 4.5. Порядком диференціального рівняння називається:
|
| a) порядок в якому записане диференціальне рівняння;
| b) порядок найвищої похідної, що входить в рівняння;
|
| c) порядок степеня функції у=f(x);
| d) порядок незалежної змінної х.
|
| 4.6. Розв’язком або інтегралом диференціального рівняння називається:
|
| a) довільна функція у=f(x);
| b) функція, яка при підстановці перетворює дане рівняння в тотожність;
|
| c) довільна функція х=f(у).
|
|
| 4.7. Частинним розв’язком диференціального рівняння n – го порядку є:
|
| a) загальний розв’язок, в який входять частинні похідні;
| b) розв’язок, що задовольняє певним початковим умовам;
|
| c) інтеграл даного диференціального рівняння.
|
|
| 4.8. Задача Коші – це:
|
| a) задача знаходження загального розв’язку;
| b) задача знаходження частинного розв’язку, що задовольняє початковим умовам;
|
| c) задача знаходження похідної функції у=f(x);
| d) задача знаходження інтегралу функції у=f(x).
|
| 4.9. Диференціальне рівняння з відокремленими змінними:
|
| a) y'=f(x);
| b)  ; ;
|
c)  . .
|
|
4.10. Рівняння виду  називаються однорідними, якщо функція називаються однорідними, якщо функція  залежить від залежить від
|
a) добутку змінних  ; ;
| b) відношення змінних  або або  ; ;
|
c) різниці змінних  ; ;
| d) суми змінних  . .
|
| 4.11. Лінійним диференціальним рівнянням першого порядку називається рівняння виду:
|
a)  ; ;
| b)  ; ;
|
c)  ; ;
| d)  . .
|
| 4.12. Бернуллі запропонував шукати розв’язок лінійного диференціального рівняння першого порядку у вигляді:
|
a)  ; ;
| b)  ; ;
|
c)  ; ;
| d)  . .
|
| 4.13. Щоб знайти розв’язок однорідного рівняння першого порядку необхідно ввести нову змінну:
|
a)  ; ;
| b)  ; ;
|
c)  ; ;
| d)  . .
|
| 4.14. Розв’язок рівняння другого порядку шукають за допомогою підстановки:
|
a)  ; ;
| b)  ; ;
|
c)  ; ;
| d)  . .
|
| 4.15. Лінійне диференціального рівняння другого порядку зі сталими коефіцієнтами:
|
a)  ; ;
| b)  ; ;
|
c)  ; ;
| d)  . .
|
| 4.16. Однорідне диференціального рівняння другого порядку зі сталими коефіцієнтами:
|
a)  ; ;
| b)  ; ;
|
c)  ; ;
| d)  . .
|
| 4.17. Частинний розв’язок однорідного диференціального рівняння другого порядку зі сталими коефіцієнтами шукають у вигляді:
|
a)  ; ;
| b)  ; ;
|
c)  ; ;
| d)  . .
|
| 4.18. Характеристичним рівнянням називають рівняння виду:
|
a)  ; ;
| b)  ; ;
|
c)  ; ;
| d)  . .
|
| 4.19. Корені характеристичного рівняння знаходять за формулою:
|
a)  ; ;
| b)  ; ;
|
c)  ; ;
| d)  . .
|
4.20. Якщо  , то загальний розв’язок однорідного диференціального рівняння має вигляд: , то загальний розв’язок однорідного диференціального рівняння має вигляд:
|
a)  ; ;
| b)  ; ;
|
c)  ; ;
| d)  . .
|
4.21. Якщо  , то загальний розв’язок однорідного диференціального рівняння має вигляд: , то загальний розв’язок однорідного диференціального рівняння має вигляд:
|
a)  ; ;
| b)  ; ;
|
c)  ; ;
| d)  . .
|
| | | |
4.22. Якщо  , то загальний розв’язок однорідного диференціального рівняння має вигляд: , то загальний розв’язок однорідного диференціального рівняння має вигляд:
| |
a)  ; ;
| b)  ; ;
| |
c)  ; ;
| d)  . .
| |
| 4.23. Диференціальне рівняння повинно містити в обов’язковому порядку:
| |
| a) похідну або диференціал функції;
| b) початкові умови;
| |
| c) набір довільних значень.
|
| |
4.24. Який порядок диференціального рівняння  ? ?
| |
| a) перший;
| b) другий;
| |
| c) третій;
| d) четвертий.
| |
| 4.25. Загальним розв’язком диференціального рівняння n–го порядку називається:
| |
| a) набір n значень аргументу х, що задовольняють дане рівняння;
| b) функція, що задовольняє дане рівняння і проходить через наперед задану точку простору;
| |
| c) функція, що перетворює дане рівняння в тотожність і містить n довільних сталих;
| d) функція, що має похідну n–го порядку.
| |
4.26. Диференціальне рівняння  називають: називають:
| |
| a) диференціальне рівняння з відокремлюваними змінними;
| b) диференціальне рівняння з сталими коефіцієнтами;
| |
| c) однорідне диференціальне рівняння;
| d) лінійне диференціальне рівняння n–го порядку.
| |
4.27. Які з нижче приведених функцій є розв’язком диференціального рівняння  ? ?
| |
a)  ; ;
| b)  ; ;
| |
c)  . .
|
| |
4.28. Які з нижче приведених функцій є розв’язком диференціального рівняння  ? ?
| |
a)  ; ;
| b)  ; ;
| |
c) 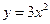 . .
|
| |
4.29. Якщо швидкість зміни шуканої величини у прямо пропорційна її абсолютному значенню:  , то: , то:
| |
a)  ; ;
| b) 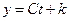 ; ;
| |
c)  ; ;
| d)  . .
| |
| де С – довільна стала; k – коефіцієнт пропорційності; t – час.
| |
4.30. Знайти загальний розв’язок диференціального рівняння з відокремлюваними змінними: 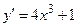 . .
| |
a)  ; ;
| b)  ; ;
| |
c)  . .
|
| |
4.31. Знайти загальний розв’язок диференціального рівняння з відокремлюваними змінними  . .
| |
a)  ; ;
| b)  ; ;
| |
c) у=  . .
|
| |
4.32. Знайти загальний розв’язок диференціального рівняння з відокремлюваними змінними  . .
| |
a)  ; ;
| b)  ; ;
| |
c)  . .
|
| |
4.33. Знайти частинний розв’язок диференціального рівняння з відокремлюваними змінними  при при 
| |
a)  ; ;
| b)  ; ;
| |
c)  . .
|
| |
4.34. Знайти частинний розв’язок диференціального рівняння з відокремлюваними змінними  при при 
| |
a)  ; ;
| b)  ; ;
| |
c)  . .
|
| |
| 4.35. Рівняння з відокремлюваними змінними:
| |
a)  ; ;
| b)  ; ;
| |
c)  . .
|
| |
4.36. Які із нижче поданих функцій є розв’язком диференціального рівняння  ? ?
| |
a)  ; ;
| b)  ; ;
| |
c)  . .
|
| |
| | 4.37. Зміна інтенсивності іонізуючого випромінювання  при проходженні через тонкий шар речовини при проходженні через тонкий шар речовини  описується диференціальним рівнянням (m – коефіцієнт послаблення випромінювання): описується диференціальним рівнянням (m – коефіцієнт послаблення випромінювання):
|
| | a)  ; ;
| b)  ; ;
|
| | c)  ; ;
| d)  . .
|
| | 4.38. Закон розчинення лікарської речовини з таблетки описується диференціальним рівнянням ( – стала розпаду таблетки): – стала розпаду таблетки):
|
| | a)  ; ;
| b)  ; ;
|
| | c)  ; ;
| d)  . .
|
| | 4.39. Кінетика хімічної реакції першого порядку описується диференціальним рівнянням:
|
| | a)  ; ;
| b)  ; ;
|
| | c)  ; ;
| d)  . .
|
| | 4.40. Кінетика хімічної реакції другого порядку описується диференціальним рівнянням:
|
| | a)  ; ;
| b)  ; ;
|
| | c)  ; ;
| d)  . .
|
| | 4.41. Однокамерна фармакокінетична модель з крапельницею описується диференціальним рівнянням:
|
| | a) 
| b) 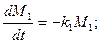
|
| | c) 
| d) 
|
| | 4.42. Вивести закон розмноження бактерій за умови, що швидкість поділу бактерій пропорційна кількості бактерій N у даний момент часу t. Початкова умова N(t=0)=N0 (k – швидкість розчинення).
|
| | a)  ; ;
| b)  ; ;
|
| | c)  ; ;
| d)  . .
|
| | 4.43. Вивести закон росту паличкоподібної клітини за умови, що швидкість її росту пропорційна довжині клітини L у даний момент часу t. Початкова умова L(t=0)=L0 (α, β – константи, що характеризують процеси синтезу і розпаду).
|
| | a)  ; ;
| b)  ; ;
|
| | c)  ; ;
| d)  . .
|
| | 4.44. Вивести закон розчинення лікарської речовини з таблетки за умови, що швидкість розчинення пропорційна кількості лікарської речовини в таблетці m у даний момент часу t. Початкова умова m(t=0)=m0.
|
| | a)  ; ;
| b)  ; ;
|
| | c) 
|
|
| | 4.45. Вивести закон для швидкості седиментації  твердих частинок в рідині за умови, що на рухому частинку діють сили тяжіння твердих частинок в рідині за умови, що на рухому частинку діють сили тяжіння  і опору середовища і опору середовища  ( ( – коефіцієнт тертя). Початкова умова – коефіцієнт тертя). Початкова умова  . Визначити граничну швидкість осідання частинок. ( . Визначити граничну швидкість осідання частинок. ( ). ).
|
| | a) 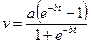 ; ;
| b)  ; ;
|
| | c)  ; ;
| d)  . .
|
| | 4.46. В однокамерній фармакокінетичній моделі диференційне рівняння, що описує зміну кількості препарату у камері, має наступний вид:
|
| | a)  ; ;
| b)  ; ;
|
| | c)  ; ;
| d)  ; ;
|
| | e)  . .
|
|
| | 4.47. Зміна концентрації препарату у крові у випадку однократного введення описується рівнянням:
|
| | a) 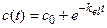 ; ;
| b)  ; ;
|
| | c)  ; ;
| d)  ; ;
|
| | e)  . .
|
|
| | 4.48. Час напіввиведення препарату в однокамерній фармакокінетичній моделі складає:
|
| | a)  ; ;
| b)  ; ;
|
| | c)  ; ;
| d)  . .
|
| | 4.49. Препарат вводиться внутрішньом’язево ( - константа подачі з депо, - константа подачі з депо,  – константа елімінації). Його концентрація у крові в момент часу – константа елімінації). Його концентрація у крові в момент часу  описується наступним рівнянням: описується наступним рівнянням:
|
| | a)  ; ;
| b)  ; ;
|
| | c)  ; ;
| d)  . .
|
| | | | | | | |