| 3.1. Функція F(x) називається первісною для функції f(x), якщо вона задовольняє умові:
|
a)  ; ;
| b)  ; ;
|
c)  ; ;
| d)  . .
|
| 3.2. Що називається невизначеним інтегралом:
|
| a) функція F (x), що має функцію f(x) своєю похідною, або f(x) dx – своїм диференціалом;
| b) сукупність всіх первісних функцій для диференціалу f (x) dx;
|
| c) сукупність всіх диференціалів функції F (x);
| d) функція f(x), що є плавною зростаючою функцією, диференціал якої F(х)dx.
|
| 3.3. Які вирази правильно визначають основні властивості невизначеного інтегралу?
|
a)  ; ;
|
b)  ; ;
|
c)  ; ;
|
d) 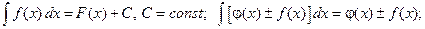
|
e)  . .
|
|
| 3.4. Виберіть правильні вирази:
|
a)  ; ;  ; ;  
| b)  ; ;  ; ; 
|
c)   
| d)  ; ;  
|
e)  ; ;   
| f)   
|
| 3.5. Безпосереднє інтегрування – це знаходження первісної з використанням…
|
| a) властивостей невизначеного інтегралу і таблиць інтегралів;
| b) переходу до іншої змінної інтегрування і спрощення підінтегрального виразу до суми інтегралів;
|
| c) спрощення підінтегрального виразу за допомогою властивостей інтегралів і таблиць похідних.
|
| 3.6. Метод інтегрування частинами ґрунтується на використанні співвідношення:
|
a)  ; ;
| b)  ; ;
|
c)  ; ;
| d)  . .
|
3.7. З геометричної точки зору невизначений інтеграл  це це
|
| a) площа криволінійної трапеції обмежена графіком функції f(x);
| b) набір парабол F(x), які відрізняються чисельним значенням сталої інтегрування С;
|
| c) набір гіпербол F(x), які відрізняються чисельним значенням сталої інтегрування С;
| d) набір кривих F(x), які відрізняються чисельним значенням сталої інтегрування С.
|
| 3.8. Виберіть вираз, що правильно визначає інтегральну суму:
|
a) 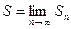 ; ;
| b) 
|
c)  ; ;
| d)  ; ;
|
e) 
|
|
| 3.9. Яке рівняння правильно описує визначений інтеграл?
|
a)  ; ;
| b)  ; ;
|
c)  ; ;
| d)  ; ;
|
e)  . .
|
|
| 3.10. Які рівняння правильно виражають властивості визначеного інтегралу?
|
a)  ; ; 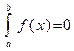 , ,  ; ;
|
b) 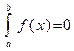 ; ;  , ,  ; ;
|
c)  , ,  , ,  ; ;
|
d)  ; ;  ; ;  . .
|
| 3.11. В чому полягає геометричний зміст визначеного інтегралу?
|
| a) В тому, що він чисельно рівний тангенсу кута нахилу дотичної в даний точці графіка.
| b) В тому, що він рівний швидкості зростання функції.
|
| c) В тому, що він чисельно рівний приросту ординати дотичної.
| d) В тому, що він чисельно рівний площі криволінійної трапеції, обмеженої графіком функції, віссю абсцис і прямими х = а, х = b.
|
| 3.12. Числове значення визначеного інтегралу підраховується за формулою
|
a)  ; ;
| b)  ; ;
|
c) 
| d) 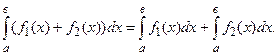
|
| 3.13. Власним називають інтеграл, якщо
|
| a) підінтегральна функція f(x) неперервна на відрізку [а, b];
| b) підінтегральна функція f(x) обмежена і неперервна на відрізку [а, b] для як завгодно великих значеннях а і b;
|
| c) підінтегральна функція f(x) обмежена і неперервна на відрізку [а, b] для скінчених значень а і b;
| d) підінтегральна функція f(x) обмежена на відрізку [а, b].
|
| 3.14. Формула прямокутників записується як:
|
a)  ; ;
|
b)  ; ;
|
c) 
|
| 3.15. Формула трапецій записується як:
|
a)  ; ;
|
b)  ; ;
|
c) 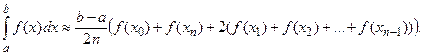
|
| 3.16. Формула Симпсона записується як:
|
a)  ; ;
|
b)  ; ;
|
c) 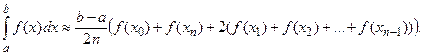
|
| 3.17. Площа криволінійної фігури обчислюється за формулою:
|
a) 
| b)  ; ;
|
c)  . .
|
|
| 3.18. Об’єм тіла обертання обчислюється за формулою:
|
a) 
| b)  ; ;
|
c)  . .
|
|
| 3.19. Довжина кривої, що є графіком функції y = f(x) на відрізку [а,b]:
|
a) 
| b) 
|
c)  . .
|
|
3.20. Обчислити інтеграл  : :
|
a)  ; ;
| b)  ; ;
|
c)  . .
|
|
3.21. Обчислити інтеграл  : :
|
| a) 0.5;
| b) 2.5
|
| c) 0;
| d) 1;
|
| e) –1.
|
|
3.22. Обчислити визначений інтеграл  : :
|
a)  ; ;
| b)  ; ;
|
c)  ; ;
| d)  ; ;
|
e)  . .
|
|
| | | | | |